\(\)
問題 6-26 の次に書かれている「高次の項(The Higher-order Terms)」の文章が少し分かりづらいと感じたので, その部分を翻訳してそれに自分なりの補足を付加したもの(補足した部分は鍵カッコで囲み灰色で色付けした)を示しておこう．
▼ 高次の項 摂動展開に於ける2次の項を見ることは興味深い．この2次の項が特に重要となるのは,注目する特定な状態 \(m\) と \(n\) に対して \(V_{mn}=0\) であるような問題のときである．そのような問題が存在するとし, さらにそのとき \(V_{kn}\neq 0\) となるような他の状態 \(k\neq n\) も存在すると仮定しよう．1次の項はゼロである．そして \(n\neq m\) である限り 0次の項もやはりゼロである．従って, この問題で遷移振幅の計算に入って来る最低次の項は 2次の項となる．[ 例えば, 第9章の荷電粒子と電磁場との相互作用の場合では, § 9.6 「Lambシフト」の議論がこの場合に相当する．従って, 「Lambシフト」での摂動補正は 2次近似 で生じるので, ここでの議論を用いる必要がある．]
ポテンシャル \(V\) が \(t\) に依存しないものとする [ 従って行列要素 \(V_{mk},V_{kn}\) は時間積分の外に出せる]．すると遷移振幅の2次の項は \(\lambda_{mn}^{(2)}\) である． 従って \(T=t_2-t_1\) とすると, それは式 (6-74) から次式となる：
\begin{align}
e^{+i(E_mt_2-E_nt_1)/\hbar}\lambda_{mn}^{(2)}&=\left(-\frac{i}{\hbar}\right)^{2}\sum_k V_{mk}V_{kn}
\int_0^{T}dt_4\,e^{i(E_m-E_k)t_4/\hbar}\int_0^{t_4}dt_3\,e^{i(E_k-E_n)t_3/\hbar}\\
&=\left(\frac{-i}{\hbar}\right)\sum_k V_{mk}V_{kn}\int_0^{T}dt_4\,e^{i\omega_{mk}t_4}
\frac{1-e^{i\omega_{kn}t_4}}{\hbar\omega_{kn}}\\
&=\sum_k \frac{V_{mk}V_{kn}}{\hbar\omega_{kn}}\left(\frac{1-e^{i\omega_{mk}T}}{\hbar\omega_{mk}}
-\frac{1-e^{i\omega_{mn}T}}{\hbar\omega_{mn}}\right)\\
&=\sum_k \frac{V_{mk}V_{kn}}{E_k-E_n}\left(\frac{e^{i(E_m-E_n)T/\hbar}-1}{E_m-E_n}
-\frac{e^{i(E_m-E_k)T/\hbar}-1}{E_m-E_k}\right)
\tag{6-98}
\end{align}
e^{+i(E_mt_2-E_nt_1)/\hbar}\lambda_{mn}^{(2)}&=\left(-\frac{i}{\hbar}\right)^{2}\sum_k V_{mk}V_{kn}
\int_0^{T}dt_4\,e^{i(E_m-E_k)t_4/\hbar}\int_0^{t_4}dt_3\,e^{i(E_k-E_n)t_3/\hbar}\\
&=\left(\frac{-i}{\hbar}\right)\sum_k V_{mk}V_{kn}\int_0^{T}dt_4\,e^{i\omega_{mk}t_4}
\frac{1-e^{i\omega_{kn}t_4}}{\hbar\omega_{kn}}\\
&=\sum_k \frac{V_{mk}V_{kn}}{\hbar\omega_{kn}}\left(\frac{1-e^{i\omega_{mk}T}}{\hbar\omega_{mk}}
-\frac{1-e^{i\omega_{mn}T}}{\hbar\omega_{mn}}\right)\\
&=\sum_k \frac{V_{mk}V_{kn}}{E_k-E_n}\left(\frac{e^{i(E_m-E_n)T/\hbar}-1}{E_m-E_n}
-\frac{e^{i(E_m-E_k)T/\hbar}-1}{E_m-E_k}\right)
\tag{6-98}
\end{align}
【 参考 】 上式は, \(\omega_{kn}=(E_k-E_n)/\hbar\) としたときの次の積分結果, 及び関係 \(\omega_{mk}+\omega_{kn}=\omega_{mn}\) を用いている：
\begin{align}
\left(\frac{-i}{\hbar}\right)\int_0^{t}dt^{‘}\,e^{i\omega_{kn} t^{‘}}&=\left(\frac{-i}{\hbar}\right)
\left[\frac{e^{i\omega_{kn}t^{‘}}}{i\omega_{kn}}\right]_0^{t}=\left(\frac{-i}{\hbar}\right)\frac{e^{i\omega_{kn}t}-1}{i\omega_{kn}}=\frac{1-e^{i\omega_{kn}t}}{\hbar\omega_{kn}}\\
&=\frac{1-e^{i(E_k-E_n)t/\hbar}}{E_k-E_n}
\end{align}
\left(\frac{-i}{\hbar}\right)\int_0^{t}dt^{‘}\,e^{i\omega_{kn} t^{‘}}&=\left(\frac{-i}{\hbar}\right)
\left[\frac{e^{i\omega_{kn}t^{‘}}}{i\omega_{kn}}\right]_0^{t}=\left(\frac{-i}{\hbar}\right)\frac{e^{i\omega_{kn}t}-1}{i\omega_{kn}}=\frac{1-e^{i\omega_{kn}t}}{\hbar\omega_{kn}}\\
&=\frac{1-e^{i(E_k-E_n)t/\hbar}}{E_k-E_n}
\end{align}
この結果の最後の因子に於ける2つの項の内, 初めの項は1次の結果で見たものと同じ時間依存性を持つ．従って, 当面2番目の項を無視すると, 結果は前と同じように「\(E_m=E_n\) を満たす状態間のみで遷移が起こる」ことになり, その確率は \(T\) に比例する．単位時間当たりの確率は式(6-86) と同様な形であり \(M_{n\to m}\) を,
\begin{equation}
M_{n\to m}=\sum_k \frac{V_{mk}V_{kn}}{E_k-E_n}
\tag{6-99}
\end{equation}
M_{n\to m}=\sum_k \frac{V_{mk}V_{kn}}{E_k-E_n}
\tag{6-99}
\end{equation}
で置き換えたものになっている．状態が連続スペクトルの中にあるものとすると, 和は積分となる．
【 参考 】 1次の場合では, 遷移振幅は式 (6-78) となるのだった：
\begin{equation}
\lambda^{(1)}_{mn}e^{i(E_mt_2-E_nt_1)/\hbar}=V_{mn}\frac{1-e^{i(E_m-E_n)T/\hbar}}{E_m-E_n}
\tag{6-78}
\end{equation}
\lambda^{(1)}_{mn}e^{i(E_mt_2-E_nt_1)/\hbar}=V_{mn}\frac{1-e^{i(E_m-E_n)T/\hbar}}{E_m-E_n}
\tag{6-78}
\end{equation}
この式で \(-V_{mn}\) を式 (6-99) で置き換えると式 (6-98) の第1項の形となる．そして遷移確率 \(P(n\to\![m])\) は1次の場合, 式 (6-85) のように \(T\) に比例し, 従って「遷移率」 \(w_{n\to\![m]}\) は式 (6-86) の形に表せるのであった：
\begin{equation}
P(n\to\,[m])=\frac{2\pi}{\hbar}\bigl|V_{mn}\bigr|^{2}\rho(E_m)T\bigg|_{E_m\simeq E_n},\quad
w_{n\to\![m]}=\frac{2\pi}{\hbar}\bigl|M_{n\to\![m]}\bigr|^{2}\,\rho(E_m)\bigg|_{E_m\simeq E_n}
\end{equation}
P(n\to\,[m])=\frac{2\pi}{\hbar}\bigl|V_{mn}\bigr|^{2}\rho(E_m)T\bigg|_{E_m\simeq E_n},\quad
w_{n\to\![m]}=\frac{2\pi}{\hbar}\bigl|M_{n\to\![m]}\bigr|^{2}\,\rho(E_m)\bigg|_{E_m\simeq E_n}
\end{equation}
この遷移確率 \(P(n\to\![m])\) と遷移率 \(w_{n\to\![m]}\) の形と式 (6-98) の第1項とを比較するならば, ただ\(|V_{mn}|^{2}\) を式 (6-99) の \(|M_{n\to m}|^{2}\) で置き換えるだけでよく, その結果式は1次のときと同様な解釈ができる訳である．
式 (6-99) が正しいのは, 初期状態 \(n\) から特定な状態 \(m\) への遷移も, また初期状態と同じエネルギーを持ったどんな状態 \(k\) への遷移も, 1次遷移では不可能であるという状況のときである．そのような状況では \(E_k=E_n\) となる状態間に対しては \(V_{kn}=0\) である [ 仮定から当然である ]．すると式 (6-98) 括弧内の第2項は決して大きくならない．なぜなら, 分母 \(E_m-E_k\) がほぼゼロでない限りこの項は大きく成り得ないが, そのとき [ 遷移は \(E_m=E_n\) を満たす状態間のみで起こり, かつ \(E_n\) と同じエネルギー状態 \(k\) への1次遷移も不可能であるとすると, 結局 \(E_m\) と同じエネルギー状態 \(k\) への1次遷移も不可能と言えるから ] 分子の \(V_{mk}\) はゼロだからである．よって全ての効果は第1項から由来するため, 式 (6-99) は正しい．さらに式 (6-98) の \(k\) についての和に於いて, \(E_k=E_m\) の所での極に曖昧さはない．なぜなら \(E_k\) がその値のときには, 分子もゼロとなるからである．
【 参考 】 原書では, 上記の青色部分が \(E_n-E_k\) 及び \(V_{kn}\) となっている．しかしこれはミスプリントではないかと思われた？ そこで, ここでは本文の記述を変更して書いたので注意する．また \(E_k\) が \(E_n\) とも \(E_m\) とも異なる場合には \(\omega_{mk}=(E_m-E_k)/\hbar\neq 0\) となるが, その場合第2項目は \(\omega_{mk}\) の増大と共に速く振動する減衰振動となり, \(T\) と共に増大する遷移確率にはやはり寄与することはない (J.J.Sakurai より)．
他方, ある状況下では, ある別の連続状態へ一次遷移出来るということも真となり得よう (例えば, 原子核は一つ以上のやり方で崩壊可能である)．そのような場合, 式 (6-99) の和は無意味である．なぜなら,「極の近傍では何をすべきか」を定義する必要があるからである．ここで助けてくれるのが式 (6-98) で無視した第2項目である．それにより \(\varepsilon\to 0\) の極限に於ける \(M_{n\to m}\) の正しい表現が, 次式となることを示してくれる (ただし一般化のために今度は 1次の項も含めている)：
\begin{equation}
M_{n\to m}=V_{m n}+\sum_{k} \frac{V_{mk}V_{kn}}{E_k – E_n – i\varepsilon}
\tag{6-100}
\end{equation}
M_{n\to m}=V_{m n}+\sum_{k} \frac{V_{mk}V_{kn}}{E_k – E_n – i\varepsilon}
\tag{6-100}
\end{equation}
これがどのようにして出てくるのかを以下で分析して行く．
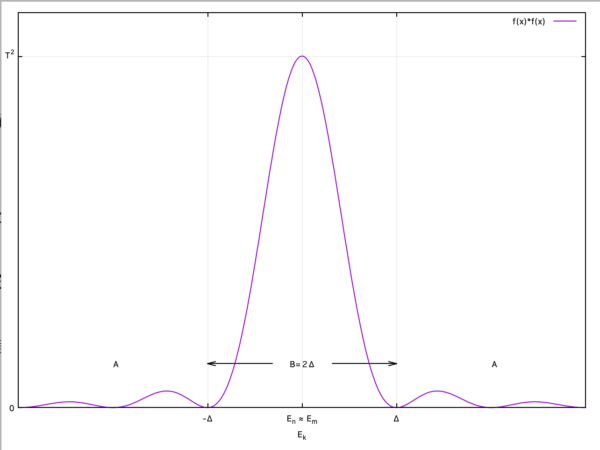
まず最初に気付くことは, 大きな \(T\) では, \(E_n\) と \(E_m\) が (\(\hbar/T\) の周りの範囲内では) 実質的に等しい場合以外では, 大きな遷移確率 (すなわち それは \(T\) に比例する) を得ることが出来ないということである．式 (6-98) の最初の項ではこれは明らかである． [ 図 6-13 を書き直した下図1 と同じような変化をするので, 摂動が印加されている時間を \(T\) とするならば, 比較的大きな確率を持つ遷移が可能なのは \(T\Delta E\sim\pi\hbar\) のときのみである．このときエネルギー変化の範囲はおよそ \(-\pi\hbar/T\le\Delta E \le \pi\hbar/T\) と言える．摂動が長い時間 \(T\) だけ掛かっているときは, ピークの幅は狭くなり, 比較的大きな確率の遷移が可能なのは近似的にエネルギーが保存されるときである．そのとき \(w=0\) の周りの中央ピークは高さが \(T^{2}\) で幅が \(1/T\) に比例しているので, その面積は大体 \(T\) に比例したものとなる]．
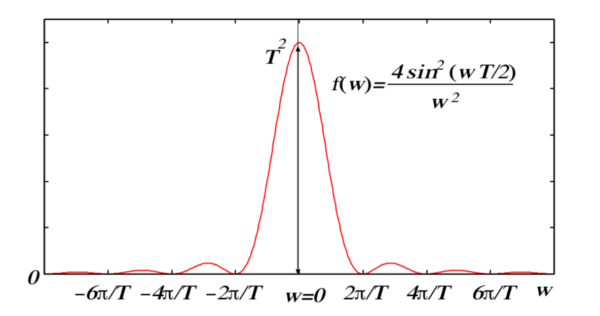
図 1. この図では, エネルギー差 \(E_m-E_n\) は変数 \(w=(E_m-E_n)/\hbar\) で置き換えてある．これらのエネルギーがほぼ等しいとき (つまり \(w\) が非常に小さいとき), 関数 \((sin^{2}wT/2)/w^{2}\) は最大値を取る．エネルギー差が大きいと, この関数は非常に小さくなる．よって, この関数を含む表式で, 最も重要な寄与は中央の \(w=0\) 周辺の領域から来る．すなわち， 2つのエネルギーがほぼ等しい領域から来るのである．
第2項目の場合では, 大きな振幅が生じるのは \(E_k\approx E_m\) のときだけである．しかしもし \(E_m\) が \(E_n\) にあまり近くない場合には, 最初の因子は, \(E_k\) が \(E_m\) に近いとき \(E_k\) の滑らかな関数である． [ 例えば, \(\Delta=E_m-E_k=E_m-E_k+E_k-E_n=x+\varepsilon\), \(x=E_k-E_n\), \(\varepsilon=E_m-E_k\) とすると, \(\Delta\) は微小ではないので \(\varepsilon\) は微小量と見做せるが \(x\) は小さくない．よって \(f(x)=V_{mk}V_{kn}/x\) は滑らかな関数と考えることが出来る．そこで \(x=E_k-E_n\) 自体は \(E_k\) に依存はするが, \(E_k\) が \(E_m\) に近くに来たときでも \(x\) は微小とはならず \(f(x)\) が急激に変化することはしない]． よって, \(E_k=E_m\) 近傍の小さな範囲ではそれをほぼ一定と見做してしまうならば,
\begin{align}
-\sum_k \left(\frac{V_{mk}V_{kn}}{E_k-E_n}\right)\frac{e^{i(E_m-E_k)T/\hbar}-1}{E_m-E_k}
&\simeq -\int dE_k\,\left(\frac{V_{mk}V_{kn}}{E_k-E_n}\right)\frac{e^{i(E_m-E_k)T/\hbar}-1}{E_m-E_k}\\
&\approx \left(\frac{V_{mk}V_{kn}}{E_k-E_n}\right)\int (-dE_k)\,\frac{e^{i(E_m-E_k)T/\hbar}-1}{E_m-E_k}
\end{align}
-\sum_k \left(\frac{V_{mk}V_{kn}}{E_k-E_n}\right)\frac{e^{i(E_m-E_k)T/\hbar}-1}{E_m-E_k}
&\simeq -\int dE_k\,\left(\frac{V_{mk}V_{kn}}{E_k-E_n}\right)\frac{e^{i(E_m-E_k)T/\hbar}-1}{E_m-E_k}\\
&\approx \left(\frac{V_{mk}V_{kn}}{E_k-E_n}\right)\int (-dE_k)\,\frac{e^{i(E_m-E_k)T/\hbar}-1}{E_m-E_k}
\end{align}
[ よって, 上式で \(\varepsilon=E_m-E_k\) とおくと, \(d\varepsilon=-dE_k\) であるから], 第2項目は, 積分量に定数を掛け合わせたものとして近似できる：
\begin{equation}
f(x)\int d\varepsilon\,\frac{e^{i\varepsilon T/\hbar}-1}{\varepsilon} = C\times \int \frac{e^{i\varepsilon T/\hbar}-1}{\varepsilon}\,d\varepsilon
\end{equation}
f(x)\int d\varepsilon\,\frac{e^{i\varepsilon T/\hbar}-1}{\varepsilon} = C\times \int \frac{e^{i\varepsilon T/\hbar}-1}{\varepsilon}\,d\varepsilon
\end{equation}
ただし \(\varepsilon=(E_m-E_k)\) は, ある微小区間, 例えば \(-\delta\) から \(+\delta\) で積分されるものとする．しかし [ 変数変換 \(y=\varepsilon T/\hbar\) を行うと \(\varepsilon=\hbar y/T\), \(d\varepsilon=\hbar dy/T\to d\varepsilon/\varepsilon=dy/y\) となるので],
\begin{align}
\int_{-\delta}^{+\delta} \big(e^{i\varepsilon T/\hbar}-1\big)\,\frac{d\varepsilon}{\varepsilon}
&=\int_{-T\delta/\hbar}^{T\delta/\hbar}\big(e^{i y}-1\big)\,\frac{dy}{y}\\
&=\int_{-T\delta/\hbar}^{T\delta/\hbar}\big(\cos y + i\sin y-1\big)\,\frac{dy}{y}\\
&=\int _{-T\delta/\hbar}^{T\delta/\hbar}\left(\frac{cos y -1}{y}+i\frac{\sin y}{y}\right)\,dy
\tag{6-101}
\end{align}
\int_{-\delta}^{+\delta} \big(e^{i\varepsilon T/\hbar}-1\big)\,\frac{d\varepsilon}{\varepsilon}
&=\int_{-T\delta/\hbar}^{T\delta/\hbar}\big(e^{i y}-1\big)\,\frac{dy}{y}\\
&=\int_{-T\delta/\hbar}^{T\delta/\hbar}\big(\cos y + i\sin y-1\big)\,\frac{dy}{y}\\
&=\int _{-T\delta/\hbar}^{T\delta/\hbar}\left(\frac{cos y -1}{y}+i\frac{\sin y}{y}\right)\,dy
\tag{6-101}
\end{align}
最初の積分は奇関数の積分なのでゼロとなる．2番目の積分は \(T\to\infty\) のとき (従って \(T\delta/\hbar\to \infty\) のとき), ある有限な極値に近づく．すなわち,
\begin{equation}
i\int_{-\infty}^{\infty} \frac{\sin y}{y}\,dy= 2i\int_{0}^{\infty}\frac{\sin y}{y}\,dy = \pi i
\end{equation}
i\int_{-\infty}^{\infty} \frac{\sin y}{y}\,dy= 2i\int_{0}^{\infty}\frac{\sin y}{y}\,dy = \pi i
\end{equation}
【 参考 】 原書では最後の結果に因子 \(2\) が書かれているがここではそれを除いた．なぜなら, 岩波の数学公式 \(\mathrm{I}\) のp.250 を参照すると, 次の公式が記してあったからである：
\begin{equation}
\def\ds#1{\mbox{${\displaystyle\strut #1}$}}
\int_{0}^{\infty} \frac{\sin ax}{x}\,dx = \begin{cases} \ds{+\frac{\pi}{2}}, & a > 0 \\ \ds{-\frac{\pi}{2}} & a<0 \end{cases}
\end{equation}
\def\ds#1{\mbox{${\displaystyle\strut #1}$}}
\int_{0}^{\infty} \frac{\sin ax}{x}\,dx = \begin{cases} \ds{+\frac{\pi}{2}}, & a > 0 \\ \ds{-\frac{\pi}{2}} & a<0 \end{cases}
\end{equation}
従って大きな遷移確率は生じない．「\(E_n\) と \(E_m\) が本質的に等しい場合にのみ, 大きな影響が生じ得る」．その場合には, \((E_k-E_n)^{-1}\) と \((E_m -E_k)^{-1}\) 由来の２つの極が二重に一致するので, そのことが第 2 項目を重要たらしめる．従って, 以下では「\(E_m\) と \(E_n\) はほぼ等しい」と仮定して分析を続けて行く．
式(6-98)中の \(k\) についての和は, 非常に小さなエネルギー \(\Delta\) を選ぶことで ２つの部分に別けることが出来る．そして和を \(|E_k-E_n|\ge \Delta\) に対する部分 \(A\) と \(|E_k-E_n|\le \Delta\) に対する部分 \(B\) とに分割する[下図2.を参照]．\(\Delta\) の大きさを選ぶには, \(E_k\) が \(E_n\) の周りでこのエネルギー範囲 \(2\Delta\) に渉って変化するときに, 因子 \(V_{mk}V_{kn}\) が感知できるほど変化しないよう十分小さいものとする．この \(\Delta\) はある有限なエネルギーであり, 時間 \(T\) は十分長く摂って \(\hbar/T \ll \Delta\) となるようにする．それは \(|E_n-E_m|\ll \Delta\) であることを意味している．
図 2. \(E_k=E_n\approx E_m\) を中心に \([-\Delta,\Delta]\) の範囲を B とし,その外側の部分を A とする．
\begin{equation}
\sum_k^{(A)} \frac{V_{mn}V_{kn}}{E_k-E_n}\frac{e^{i(E_m-E_n)T/\hbar}-1}{E_m-E_n}
\equiv a\,\frac{e^{ix}-1}{x}\frac{T}{\hbar}
\tag{6-102}
\end{equation}
\sum_k^{(A)} \frac{V_{mn}V_{kn}}{E_k-E_n}\frac{e^{i(E_m-E_n)T/\hbar}-1}{E_m-E_n}
\equiv a\,\frac{e^{ix}-1}{x}\frac{T}{\hbar}
\tag{6-102}
\end{equation}
ただし,
\begin{equation}
x=\frac{E_m-E_n}{\hbar}T,\quad a=\sum_{k}^{(A)}\frac{V_{mk}V_{kn}}{E_k-E_n}
\end{equation}
x=\frac{E_m-E_n}{\hbar}T,\quad a=\sum_{k}^{(A)}\frac{V_{mk}V_{kn}}{E_k-E_n}
\end{equation}
和は \(E_m\) の \(\pm \Delta\) 以内を除く全ての \(E_k\) に及ぶ．この和は \(\Delta\) には殆ど依存しない．そして \(\Delta\to0\) のとき「主値積分」( principal-value integral ) の定義となる．即ち, 極限 \(\Delta\to0\) で次のように書くことが出来る：
\begin{equation}
a = V_{mn}+\sum_k V_{mk}V_{kn}\,\mathrm{P.P.}\,\frac{1}{E_k-E_n}
\tag{6-103}
\end{equation}
a = V_{mn}+\sum_k V_{mk}V_{kn}\,\mathrm{P.P.}\,\frac{1}{E_k-E_n}
\tag{6-103}
\end{equation}
ただし P.P. は主値部分を表している[前ブログ記事「複素積分の公式について」を参照のこと]．そして1次の項 \(V_{mn}\) を回復させた．これは \(V_{mn}\) がゼロとならない場合を考慮したからである．
次に領域 \(B\) の場合であるが, この場合の \(V_{mk}V_{kn}\) は,「\(E_k-E_m=0\) のときの値であり一定である」と考える(take)．[そして前と同様に, 和は積分に置き換えて考える]：
\begin{align}
\sum_{k}^{(B)}V_{mk}V_{kn}F(E_k)&=\sum_k^{(B)} \frac{V_{mk}V_{kn}\delta(E_k-E_m)}{E_k-E_n}\left(
\frac{e^{i(E_m-E_n)T/\hbar}-1}{E_m-E_n} – \frac{e^{i(E_m-E_k)T/\hbar}-1}{E_m-E_k}\right)\\
&\rightarrow
\int dE_k\,\frac{V_{mk}V_{kn}\delta(E_k-E_m)}{E_k-E_n}\left(\frac{e^{i(E_m-E_n)T/\hbar}-1}{E_m-E_n}
– \frac{e^{i(E_m-E_k)T/\hbar}-1}{E_m-E_k}\right)
\end{align}
\sum_{k}^{(B)}V_{mk}V_{kn}F(E_k)&=\sum_k^{(B)} \frac{V_{mk}V_{kn}\delta(E_k-E_m)}{E_k-E_n}\left(
\frac{e^{i(E_m-E_n)T/\hbar}-1}{E_m-E_n} – \frac{e^{i(E_m-E_k)T/\hbar}-1}{E_m-E_k}\right)\\
&\rightarrow
\int dE_k\,\frac{V_{mk}V_{kn}\delta(E_k-E_m)}{E_k-E_n}\left(\frac{e^{i(E_m-E_n)T/\hbar}-1}{E_m-E_n}
– \frac{e^{i(E_m-E_k)T/\hbar}-1}{E_m-E_k}\right)
\end{align}
即ち, \(\sum_{k}^{(B)}V_{mk}V_{kn}F(E_k)\) を次で置き換え, これを \(bI\) と書くことにする：
\begin{equation}
\left[\sum_k V_{mk}V_{kn}\,\delta(E_k-E_m)\right]\int_{E_m-\Delta}^{E_m+\Delta}F(E_k)\,dE_k \equiv b\,I
\tag{6-104}
\end{equation}
\left[\sum_k V_{mk}V_{kn}\,\delta(E_k-E_m)\right]\int_{E_m-\Delta}^{E_m+\Delta}F(E_k)\,dE_k \equiv b\,I
\tag{6-104}
\end{equation}
ただし, [ \(E_n\) と \(E_m\) は本質的に等しいので ]
\begin{equation}
b = \sum_k V_{mk}V_{kn}\,\delta(E_k-E_m)= \sum_k V_{mk}V_{kn}\,\delta(E_k-E_n)
\tag{6-105}
\end{equation}
b = \sum_k V_{mk}V_{kn}\,\delta(E_k-E_m)= \sum_k V_{mk}V_{kn}\,\delta(E_k-E_n)
\tag{6-105}
\end{equation}
そして,
\begin{equation}
I = \int_{E_m-\Delta}^{E_m+\Delta}\frac{dE_k}{E_k-E_n}
\left(\frac{e^{i(E_m-E_n)T/\hbar}-1}{E_m-E_n}- \frac{e^{i(E_m-E_k)T/\hbar}-1}{E_m-E_k}\right)
\tag{6-106}
\end{equation}
I = \int_{E_m-\Delta}^{E_m+\Delta}\frac{dE_k}{E_k-E_n}
\left(\frac{e^{i(E_m-E_n)T/\hbar}-1}{E_m-E_n}- \frac{e^{i(E_m-E_k)T/\hbar}-1}{E_m-E_k}\right)
\tag{6-106}
\end{equation}
さてここで \((E_m-E_n)(T/\hbar)=x\) そして \((E_k-E_n)(T/\hbar)=y\) とおく．
すると,
\begin{align}
&(E_m-E_k)\frac{T}{\hbar}=(E_m-E_n+E_n-E_k)\frac{T}{\hbar}=
(E_m-E_n)\frac{T}{\hbar}-(E_k-E_n)\frac{T}{\hbar}=x-y,\\
&\frac{dE_k(T/\hbar)}{(E_k-E_n)(T/\hbar)}=\frac{dy}{y},\quad
\frac{1}{E_m-E_n}=\left(\frac{T}{\hbar}\right)\frac{1}{x},\quad
\frac{1}{E_m-E_k}=\left(\frac{T}{\hbar}\right)\frac{1}{x-y},\\
&E_k-E_m\simeq E_k-E_n=\pm\Delta\ \rightarrow\ y=(E_k-E_n)\frac{T}{\hbar}=\pm\Delta\frac{T}{\hbar}
\end{align}
&(E_m-E_k)\frac{T}{\hbar}=(E_m-E_n+E_n-E_k)\frac{T}{\hbar}=
(E_m-E_n)\frac{T}{\hbar}-(E_k-E_n)\frac{T}{\hbar}=x-y,\\
&\frac{dE_k(T/\hbar)}{(E_k-E_n)(T/\hbar)}=\frac{dy}{y},\quad
\frac{1}{E_m-E_n}=\left(\frac{T}{\hbar}\right)\frac{1}{x},\quad
\frac{1}{E_m-E_k}=\left(\frac{T}{\hbar}\right)\frac{1}{x-y},\\
&E_k-E_m\simeq E_k-E_n=\pm\Delta\ \rightarrow\ y=(E_k-E_n)\frac{T}{\hbar}=\pm\Delta\frac{T}{\hbar}
\end{align}
従って次を得る：
\begin{equation}
I=\frac{T}{\hbar}\int_{-T\Delta/\hbar}^{+T\Delta/\hbar}
\frac{dy}{y}\left(\frac{e^{ix}-1}{x}-\frac{e^{i(x-y)}-1}{x-y} \right)
\tag{6-107}
\end{equation}
I=\frac{T}{\hbar}\int_{-T\Delta/\hbar}^{+T\Delta/\hbar}
\frac{dy}{y}\left(\frac{e^{ix}-1}{x}-\frac{e^{i(x-y)}-1}{x-y} \right)
\tag{6-107}
\end{equation}
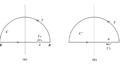
この積分は \(y\) を複素変数と見做した周積分 (contour integral) を考え, 閉曲線を変化させることで非常に容易に評価することが出来る．\(-T\Delta/\hbar\) から \(T\Delta/\hbar\) までの直線上の積分の代わりに, 実軸より下を通る半径 \(T\Delta/\hbar\) の半円上の積分に移る(go on)．\(T\Delta/\hbar\) は非常に大きいので, 第2項の寄与は無視できる．従って, この閉曲線上で [ \(f(x)=1\) の場合を考えると, そのときの主値はゼロなので]
\begin{align}
&\oint_C \frac{f(z)}{z-a}dz=\mathrm{P}\int_{-\infty}^{\infty}\frac{f(x)}{x-a}dx ＋i\pi f(a),
\quad \rightarrow \int_{-\infty}^{\infty} \frac{1}{x-a}dx = 0+i\pi=i\pi \\
&\Rightarrow\quad
\int_{-T\Delta/\hbar}^{T\Delta/\hbar} \frac{dy}{y}\approx\int_{-\infty}^{\infty}\frac{dy}{y}=i\pi
\end{align}
&\oint_C \frac{f(z)}{z-a}dz=\mathrm{P}\int_{-\infty}^{\infty}\frac{f(x)}{x-a}dx ＋i\pi f(a),
\quad \rightarrow \int_{-\infty}^{\infty} \frac{1}{x-a}dx = 0+i\pi=i\pi \\
&\Rightarrow\quad
\int_{-T\Delta/\hbar}^{T\Delta/\hbar} \frac{dy}{y}\approx\int_{-\infty}^{\infty}\frac{dy}{y}=i\pi
\end{align}
となるので \(I\) は次となる：
\begin{equation}
I\approx \frac{T}{\hbar}\frac{e^{ix}-1}{x}\int_{-T\Delta/\hbar}^{T\Delta/\hbar} \frac{dy}{y}
=i\pi\frac{T}{\hbar}\frac{e^{ix}-1}{x}
\end{equation}
I\approx \frac{T}{\hbar}\frac{e^{ix}-1}{x}\int_{-T\Delta/\hbar}^{T\Delta/\hbar} \frac{dy}{y}
=i\pi\frac{T}{\hbar}\frac{e^{ix}-1}{x}
\end{equation}
部分 A と部分 B とを一緒にすることで, [即ち式 (6-102) と式 (6-105) 及び式 (6-107) から振幅は \(x\ll 1\) として] 次となる：
\begin{align}
a\,\frac{e^{ix}-1}{x}\frac{T}{\hbar}+bI&=a\frac{T}{\hbar}\frac{e^{ix}-1}{x}+i\pi b\,\frac{T}{\hbar}
\frac{e^{ix}-1}{x}\notag\\
&=(a+i\pi b)\frac{T}{\hbar}\frac{e^{ix}-1}{x}
\tag{6-108}
\end{align}
a\,\frac{e^{ix}-1}{x}\frac{T}{\hbar}+bI&=a\frac{T}{\hbar}\frac{e^{ix}-1}{x}+i\pi b\,\frac{T}{\hbar}
\frac{e^{ix}-1}{x}\notag\\
&=(a+i\pi b)\frac{T}{\hbar}\frac{e^{ix}-1}{x}
\tag{6-108}
\end{align}
[ここで, 式中の因子 \((T/\hbar)(e^{ix}-1)/x\) は \(x=(E_m-E_n)T/\hbar\) であった．更に, このとき \(E_m\approx E_n\) であったから \(E_m-E_n\approx x, (x\ll 1)\) と近似しても構わないであろう．更にまた, 式 (6-86) では \(M_{n\to m}\) の絶対値を取るので虚数単位 \(i\) は無視してしまってよい．すると,]
\begin{align}
&\frac{T}{\hbar}\frac{e^{ix}-1}{x}=\frac{e^{ix}-1}{E_m-E_n}\approx \frac{e^{ix}-1}{x}
\simeq i \quad (x\ll 1),\\
&\Rightarrow\quad (a+i\pi b)\frac{T}{\hbar}\frac{e^{ix}-1}{x}\approx (a+i\pi b)i
\rightarrow a+i\pi b
\end{align}
&\frac{T}{\hbar}\frac{e^{ix}-1}{x}=\frac{e^{ix}-1}{E_m-E_n}\approx \frac{e^{ix}-1}{x}
\simeq i \quad (x\ll 1),\\
&\Rightarrow\quad (a+i\pi b)\frac{T}{\hbar}\frac{e^{ix}-1}{x}\approx (a+i\pi b)i
\rightarrow a+i\pi b
\end{align}
これにより, 式 (6-86) の形の遷移確率は \(M_{n\to m}\) を次としたものとなる：
\begin{align}
M_{n\to m}&=a+i\pi b
=V_{mn}+\sum_{k}V_{mk}V_{kn}\mathrm{P.P.}\frac{1}{E_k-E_n}+i\pi \sum_{k}V_{mk}V_{kn}\delta(E_k-E_n)\\
&=V_{mn}+\sum_{k}V_{mk}V_{kn}\left[ \mathrm{P.P.}\,\frac{1}{E_k-E_n} + i\pi\delta(E_k-E_n) \right]
\tag{6-109}
\end{align}
M_{n\to m}&=a+i\pi b
=V_{mn}+\sum_{k}V_{mk}V_{kn}\mathrm{P.P.}\frac{1}{E_k-E_n}+i\pi \sum_{k}V_{mk}V_{kn}\delta(E_k-E_n)\\
&=V_{mn}+\sum_{k}V_{mk}V_{kn}\left[ \mathrm{P.P.}\,\frac{1}{E_k-E_n} + i\pi\delta(E_k-E_n) \right]
\tag{6-109}
\end{align}
最後の鍵カッコ部分は, \(\varepsilon\to0\) の極限で \((E_k-E_m-i\varepsilon)^{-1}\) と書くことが出来る．[前ブログ「複素積分の公式について」の式(9)で \(x\to E_k,\,a\to E_n\) とした場合になる]：
\begin{equation}
\lim_{\varepsilon\to0}\frac{1}{x-a-i\varepsilon}
=\mathrm{P}\frac{1}{x-a}\,dx + i\pi\delta(x-a)
\tag{9}
\end{equation}
\lim_{\varepsilon\to0}\frac{1}{x-a-i\varepsilon}
=\mathrm{P}\frac{1}{x-a}\,dx + i\pi\delta(x-a)
\tag{9}
\end{equation}
よって \(M_{n\to m}\) は, 式 (6-100) の形に書くことが出来たことになる：
\begin{align}
M_{n\to m}&=V_{mn}+\sum_{k}V_{mk}V_{kn}\left[ \mathrm{P.P.}\,\frac{1}{E_k-E_n} + i\pi\delta(E_k-E_n) \right]\\
&=V_{mn}+\sum_{k}V_{mk}V_{kn}\frac{1}{E_k-E_n-i\varepsilon}
\tag{6-100}
\end{align}
M_{n\to m}&=V_{mn}+\sum_{k}V_{mk}V_{kn}\left[ \mathrm{P.P.}\,\frac{1}{E_k-E_n} + i\pi\delta(E_k-E_n) \right]\\
&=V_{mn}+\sum_{k}V_{mk}V_{kn}\frac{1}{E_k-E_n-i\varepsilon}
\tag{6-100}
\end{align}
式 (6-100) から, \(n\) から \(m\) への直接的な遷移がそのときには不可能であっても,「仮想状態」(virtual state)と呼ばれる状態を通じて遷移は可能であることが分かる．即ち, 系は \(n\) から \(k\) へ, そして \(k\) から \(m\) へと遷移すると考えることが出来る．
間接的な遷移過程の遷移振幅は式 (6-99) で与えられている．「系は実際に一つまたは別の中間状態 \(k\) を経るというのではなく, むしろ量子力学に特徴的なこととして、様々な中間状態 \(k\) を経る振幅があって, その寄与が干渉を起こすと言うのが正しい」ことに注意する．
中間状態は始状態や終状態と同じエネルギー状態ではない．しかしエネルギー保存は破掟していない．なぜなら, 仮想状態は永久的に占有されるものではないからである．和への寄与の強さは, このエネルギー不一致量(discrepancy) に反比例して変化する．
これらの中間状態に絶対的なものは全く存在しない．それは, \(V\) を系 \(H\) の摂動と考え, \(H+V\) の真の状態について \(H\) だけの状態で表現して見れば分かることである．無摂動問題と摂動問題の区別を別の仕方で行ったならば,その処方には異なる公式と中間状態が現れるであろう．
ポテンシャルが時間に (例えば周期的に) 依存する場合には, 多くの興味深い効果が起こる(result)．それらのほとんどは, マイクロ波実験に於いて観測される．その場合の摂動 \(V(\mathbf{x},t)\) は, 周期的な時間変化をする弱い電場または磁場である．
