汎関数微分と方向微分

\(\)
第７章では「汎関数微分」を導入して議論が為されている．「汎関数微分」は少し分かりづらいと感じたのでその補足として Swanson の文章とウィキペディアの説明文を紹介しておこう．

---

(1) 先ずは、Mark S. Swanson : 「Path Integrals and Quantum Proceses」の § 1.3 の一部を抜粋したものを示す：
実関数は, ある空間から実数へのマッピングである．関数自身は無限大次元空間に於ける点と見做すことが出来る．この類似性から, 「汎関数」( functional )を「関数または関数多項式の数値へのマッピングである」と定義する．関数は汎関数によってマッピングされた座標の役割 (通常の関数 \(f(x)\) での座標 \(x\) の役割) を果たす．汎関数を構築する標準的な方法は, 引数のある区間について関数の集団及びそれらの積を積分することである．
汎関数を歴史的極限とする関数の性質を決定することで変分計算が生まれた ( Determining the nature of the functions that extremize the functional historically led to the calculus of variations )．関数の極値を見出す問題との類推から ( by analogy to ), 関数の極限形を決定するには汎関数微分及び汎関数微分係数を定義する必要がある．一度これらの定義が為されると, 極限関数が満たしておくべき局所的な候補または各点ごとの候補を生成することが可能となる (it is possible to create a local or pointwise criterion that extremum functions must satisfy)．[ 日本語ウィキによれば, ある汎関数が, その勾配やラプラシアン或いは他の高階微分に依存しないとき, その汎関数は局所的(local)であると言うらしい ]．この定義を行うために, 先ずは最も簡単な場合で考察する．そこで, 単一の関数 \(g(x)\) だけで構成される一般的な関数を \(\mathcal{F}[g(x)]\) と書くことにする．すると \(g(x)\) に関する \(\mathcal{F}\) の汎関数微分は次のような公式により定義される：

ただし \(\delta(x-y)\) は積分の次元に合う適切な次元の Dirac のデルタ関数である．
式 (sw-1) の定義は, 通常の微分操作が有する特性を全て持っている．例えば, もし \(\mathcal{F}\) と \(\mathcal{G}\) が2つの汎関数であるならば, それらの積の汎関数微分は次のような Leibniz 特性となる：

\(\mathcal{F}[g]\) が \(g=0\) 周辺の関数空間の区間でよい振舞いをする( well-behaved )汎関数である場合, 汎関数 \(\mathcal{F}\) は次のようなテイラー級数表示で示すことが出来る：

ただしこれ以降では, 積分端　( limits of integration ) の明示はしないことにする．式 (sw-3) の両辺に任意のベキの汎関数微分を作用させて \(g=0\) での結果を評価することで, 式 (sw-3) が自己無矛盾であることが示される．他の関数 \(f\) 周辺での汎関数 \(\mathcal{F}[g]\) のテイラー級数展開も定義出来て, 次となるであろう：

任意の汎関数は, その汎関数微分が性質の良いような( well-defined )関数による式 (sw-4) の形式によって展開することが可能である．
式 (sw-4) は汎関数微分の定義も可能とする．関数 \(g(x)\) からの無限小の逸脱 (infinitesimal deviation) を \(\delta g(x)\) とする．すなわち関数 \(g(x)+\delta g(x)\) は全ての場所で \(g(x)\) の無限小近傍に存在する．すると, 汎関数の 1 次までのテイラー級数展開の式 (SW-4) は次を与える：

ただしオーダー \((\delta g)^{2}\) 以上の項は問題とならないので記してない．
また, 引数である関数 \(g(x)\) が無限小変化 \(\delta g\) する場合, 汎関数 \(\mathcal{F}\) の無限小変化 (微分) \(\delta \mathcal{F}\) は, 次で定義できるであろう：

この定義は, 通常の多変数関数の微分と形式的に全く類似している．そこでの関数 \(f(\mb{x})\) の微分は, 座標の任意な変化 \(d\mb{x}\) の下での関数の変化として定義される．従って \(f(\mb{x})\) の微分は次のようにかかれる：

ただし \(\nabla\) は勾配演算子である．関数空間においては, 区間 \([-L,L]\) を周期とする周期関 \(f(x)\) と \(g(x)\) の内積が,

で表されることを考えるならば, 式 (sw-6) の積分は「関数 \(\delta\mathcal{F}/\delta x\) と関数 \(\delta g\) の内積である」と見做すことが出来る．従って, 式 (sw-6) と式 (sw-7) を等価なものと見做すならば,『\(\delta g(x)\) は \(d\mb{x}\) の役割を果たしており, 汎関数微分 \(\displaystyle{\frac{\delta\mathcal{F}}{\delta g(\theta)}}\) は事実上, 汎関数の勾配である』と言える．
汎関数のチェーン・ルール (合成関数の微分則) は, 汎関数 \(\mathcal{F}[g]\) の \(g\) を 更に\(f\) の汎関数, 従って \(g=g[f]\) と考えることで構築できる．2つの微分操作を連続して行うと次となる：

上式と微分の標準的な形 (sw-6) との比較から, 次のようなチェーン・ルールが成り立つと言える：

これら全ての定義を一つ以上の関数の汎関数の場合に拡張するのは誠に容易である．一般的な場合, 汎関数 \(\mathcal{F}\) はその引数に関数の集合 \({g_i(x)}\) を持つ．表記を容易にするために,それらは下付き添字で指示(インデックス)される．この時点で,「和の慣習」(summation convention)を導入すると便利である．その慣習では, 「式中に同じ添字が現れたときには添字の全範囲での和をとることを表している」と理解する．ただし添字の一方がカッコ内にある場合は除くものとする．例として, ２つの \(n\)-次元実ベクトル \(\mb{x}\) と \(\mb{y}\) の内積は, デカルト座標で次のように書かれる：

しかしながら, 表現式 \(\lambda^{(i)}x_i\) では和を表現しているわけではなく, ただの \(\lambda^{(i)}\) と \(x_i\) の積である．混乱する危険がある場合には, 和は明示的に記される．和の慣習を用いると,多数の関数の汎関数に対する汎関数微分は次のように書かれることになる：

ただし添字 \(j\) について和は \(1\) から \(n\) まで取るものとする．
(2)　次は, 日本語のウィキペディアの記述である：

数学及び理論物理学に於ける汎関数微分(functional derivative)は,「方向微分」(directional derivative)の一般化である．方向微分が有限次元のベクトルに関する微分法であるのに対して, 汎関数微分は (無限次元ベクトルとしての)連続関数に対する微分法を与えるとされるが, 単純な1変数微分積分学に於ける1次元の微分を一般化したものと見做せる点では共通している．汎関数微分の数学的に厳密な取り扱いは関数解析学に属する．

そして汎関数の定義式として次式が提示される：

\(F\) の汎関数微分 \(\displaystyle{\frac{\delta F}{\delta \phi}}\) とは, 任意の試験関数 \(f\) に対して次式を満たすようなシュバルツ超関数を言う：

\begin{align}
\left\langle \frac{\delta F[\phi(x)]}{\delta \phi(x)}, f(x)\right\rangle
&= \int \frac{\delta F[\phi(x)]}{\delta \phi(x’)}f(x’)\,dx’\\
&=\lim_{\varepsilon\to 0}\frac{F[\phi(x)+\varepsilon f(x)]-F[\phi(x)]}{\varepsilon}\\
&=\frac{d}{d\varepsilon}F[\phi+\varepsilon f]\Bigg|_{\varepsilon=0}
\tag{1}
\end{align}

ただし左辺の記号 \(\langle a,b\rangle\) は \(a\) と \(b\) の内積を表している．試験関数 \(f\) の処に \(\phi\) の第1変分 \(\delta \phi\) を代用して, 汎関数 \(F\) の微分( differential )すなわち 第1変分( first variation ) \(\delta F\) が得られることは, 傾き( gradient )から関数の微分が得られるのと同様である：

\begin{align}
d\phi &=(\nabla \phi)\cdot d\mb{r}=\ppdiff{\phi}{x}dx +\ppdiff{\phi}{y}dy+\ppdiff{\phi}{z}dz\\
\rightarrow\quad&\delta F=\left\langle \frac{\delta F[\phi(x)]}{\delta \phi(x)},\delta \phi \right\rangle
=\int \frac{\delta F[\phi(x)]}{\delta \phi(x’)}\,\delta \phi(x’)\,dx’
\tag{2}
\end{align}

また, ノルム \(1\) の試験関数 \(f\) を用いれば, この関数に沿った方向微分が得られる．

更に, 汎関数微分の例として, 関数とその導関数を含む式の積分として書けるような汎関数に対する汎関数微分の公式を挙げている．それは「オイラー=ラグランジュ方程式の一般化」であるそうだ．

与えられた汎関数が次の形をしているとする：

\begin{equation}
F[\rho(\mb{r})]=\int f(\mb{r},\rho(\mb{r}),\nabla \rho(\mb{r}))\,d\mb{r}
\tag{3}
\end{equation}

ただし \(\rho\) が \(\mb{r}\) の境界で消えるものとする．すると, 汎関数微分と試験関数 \(\phi\) との内積は次の形に書くことが出来る：

\begin{align}
\left\langle \frac{\delta F[\rho]}{\delta \rho},\phi\right\rangle
&= \frac{d}{d\varepsilon}\int f(\mb{r},\rho+\varepsilon\phi,\nabla\rho + \varepsilon\nabla\phi)\,d\mb{r}\Bigg|_{\varepsilon=0}\\
&=\int \left(\ppdiff{f}{\rho}\phi+\ppdiff{f}{\nabla \rho}\cdot\nabla\phi\right)d\mb{r}\\
&=\int \left[\ppdiff{f}{\rho}\phi+\nabla\cdot\left(\ppdiff{f}{\nabla \rho}\phi\right)-\left(\nabla\cdot\ppdiff{f}{\nabla\rho}\right)\phi\right]d\mb{r}\\
&=\int \left[\ppdiff{f}{\rho}\phi-\left(\nabla\cdot\ppdiff{f}{\nabla \rho}\right)\phi\right]d\mb{r}\\
&=\left\langle \ppdiff{f}{\rho}-\nabla\cdot\ppdiff{f}{\nabla\rho},\,\phi\right\rangle
\tag{4}
\end{align}

ここで, 3行目は積分の限界に於いて \(\phi=0\) と仮定した．故に, 汎関数微分は次となる：

\begin{equation}
\frac{\delta F[\rho]}{\delta\rho} = \ppdiff{f}{\rho}-\nabla\cdot\ppdiff{f}{\nabla\rho}
\tag{5}
\end{equation}

テル・ハール：「解析力学」では, この式 (5) を以って汎関数微分の導入としている：

(3)　「汎関数微分は方向微分の一般化である」ことが分かったので, 参考のためにその「方向微分」について, 安達：「ベクトル解析」§ 32. から抜粋した文章を示しておく．
スカラー点関数を \(\phi(x,y,z)\) とし, 点 P に於けるスカラーの値を \(\phi\), P からある方向に引かれた直線 \(g\) 上で, P の近くの点 P’ に於けるスカラーの値を \(\phi+\Delta \phi\) とする．いま, PP’\(=\Delta s\) と置き, 直線 \(g\) 上で P’ を P に限りなく近づけたときの \(\Delta \phi/\Delta s\) の極限値を次のように書く：

\(\displaystyle{\frac{\Delta \phi}{\Delta s}}\) は \(\Delta s\) に対する \(\phi\) の値の変化する割合であるから, \(\displaystyle{\frac{\partial\phi}{\partial s}}\) は \(g\) 方向に対する \(\phi\) の値の変化率である．この\(\displaystyle{\frac{\partial\phi}{\partial s}}\) を, 点 P に於ける \(g\) 方向に対する \(\phi\) の「方向微分係数」という．

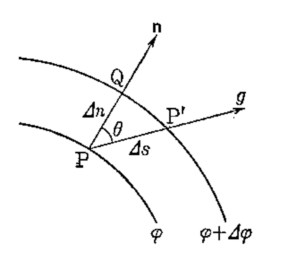
P, P’ の座標を \((x,y,z)\), \((x+\Delta x, y+\Delta y, z+\Delta z)\) とすれば, 近似的に次が言える：

ここで, \(\displaystyle{\frac{\Delta x}{\Delta s}, \frac{\Delta y}{\Delta s}, \frac{\Delta z}{\Delta s}}\) は直線 \(g\) の方向余弦であるから, これらを \(l,m,n\) とすれば, 上式は \(\Delta s\to 0\) の極限で次である：

ゆえに, \(g\) 方向に対する方向微分係数は \(\Delta \phi\) の \(g\) 方向に対する成分に等しい．　また, \(\nabla\phi\) と直線 \(g\) の成す角度を \(\theta\) とすれば, 上式から

よって, \(g\) の方向が \(\nabla\phi\) の方向と一致するとき \(\cos\theta=1\) となるから,「\(\nabla\phi\) の方向に対する \(\phi\) の方向微分係数が最大で, その値は \(\big|\nabla\phi\big|\) に等しい」．また, 等位面に沿っては \(\phi\) の値は一定であるから \(d\phi=\nabla\phi\cdot d\mb{r}=0\) である．従って, \(\nabla\phi\) は等位面上の任意の線要素 \(d\mb{r}\) に垂直, すなわち「\(\nabla\phi\) は等位面に垂直である」．
直線 \(g\) の方向の単位ベクトルを \(\mb{u}\) とすれば, \(g\) 方向に対する \(\phi\) の方向微分係数は, \(\nabla\phi\) の \(g\) 方向に対する成分であるから, それは \(\mb{u}\) と \(\nabla\phi\) の内積で表される．\(g\) の方向余弦すなわち \(\mb{u}\) の成分は \(l,m,n\) であるから,