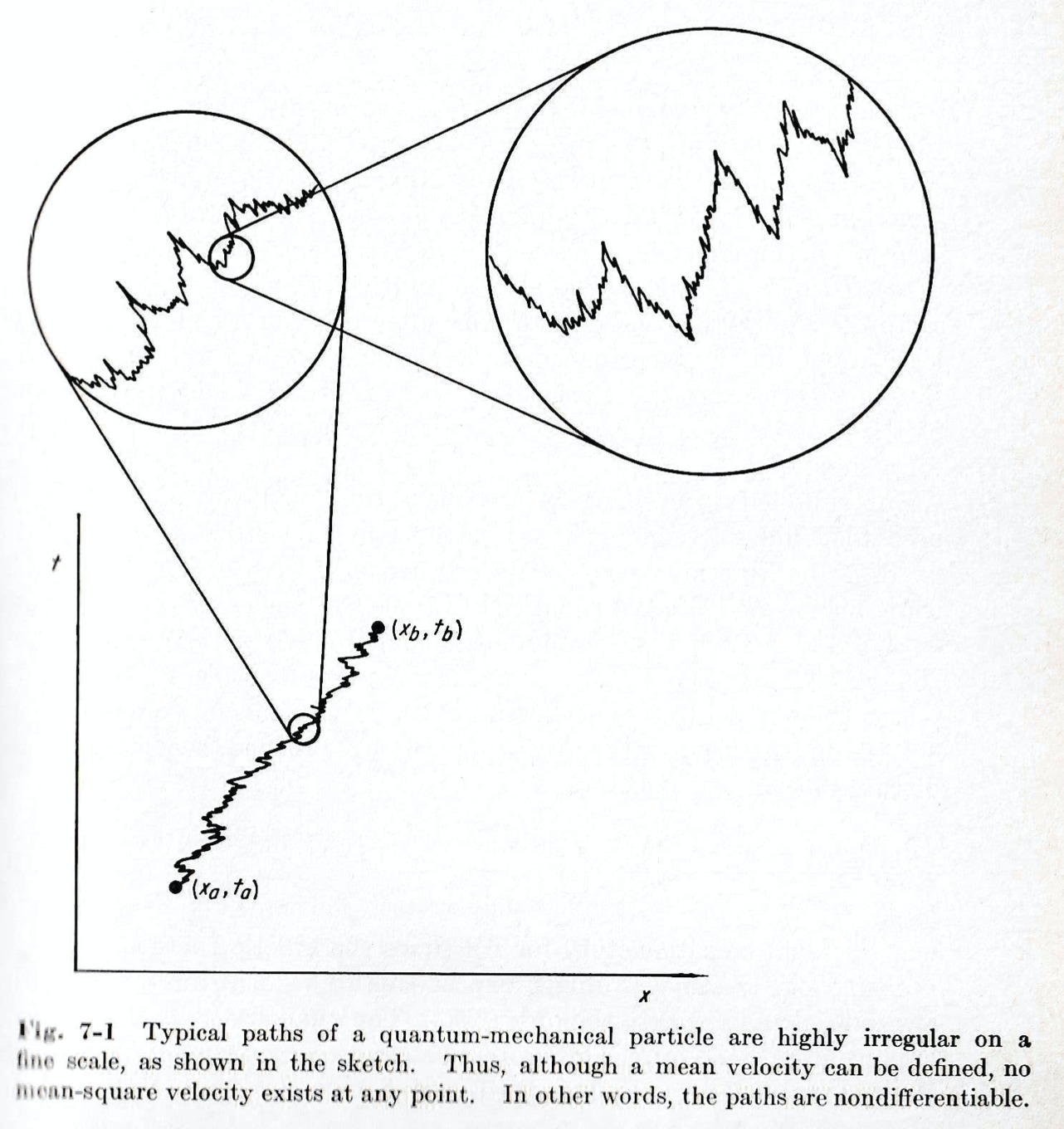
\(\)
ファインマンは第７章の§ 7-3 の処で, 以下のように述べている：
式 (7-45) からは, 更なる結果を導出することが出来る．それは量子力学に於いて重要な「経路の特性」をより良く認識する手助けとなるであろう．次の2つの項を考えよう：
\begin{align}
&\left\langle\,x_k\,m\frac{x_k-x_{k-1}}{\varepsilon}\,\right\rangle \tag{7-46}\\
&\left\langle\,x_{k+1}\,m\frac{x_{k+1}-x_k}{\varepsilon}\,\right\rangle \tag{7-47}
\end{align}
&\left\langle\,x_k\,m\frac{x_k-x_{k-1}}{\varepsilon}\,\right\rangle \tag{7-46}\\
&\left\langle\,x_{k+1}\,m\frac{x_{k+1}-x_k}{\varepsilon}\,\right\rangle \tag{7-47}
\end{align}
これら2つの項の差は \(\varepsilon\) の程度である．なぜなら, それらは同じ量であり \(\varepsilon\) の区間だけ異なる時刻で計算されたものであるからである．従って, 式 (7-47) を式 (7-45) の第2項の代わりに使ってよい(be justified in substituting)．すると, 結果は次となる：
\begin{align}
&\left\langle\,m\frac{x_{k+1}-x_k}{\varepsilon}\,x_k\,\right\rangle
-\left\langle\,x_k\,m\frac{x_k-x_{k-1}}{\varepsilon}\,\right\rangle\\
&\quad=\left\langle\,m\frac{x_{k+1}-x_k}{\varepsilon}\,x_k\,\right\rangle
-\left\langle\,x_{k+1}\,m\frac{x_{k+1}-x_k}{\varepsilon}\,\right\rangle\\
&\quad=\left\langle\,m\frac{x_{k+1}-x_k}{\varepsilon}\bigl(x_k- x_{k+1}\bigr)\,\right\rangle\\
&\quad=\frac{\hbar}{i}\left\langle\,1\,\right\rangle \tag{7-48}
\end{align}
&\left\langle\,m\frac{x_{k+1}-x_k}{\varepsilon}\,x_k\,\right\rangle
-\left\langle\,x_k\,m\frac{x_k-x_{k-1}}{\varepsilon}\,\right\rangle\\
&\quad=\left\langle\,m\frac{x_{k+1}-x_k}{\varepsilon}\,x_k\,\right\rangle
-\left\langle\,x_{k+1}\,m\frac{x_{k+1}-x_k}{\varepsilon}\,\right\rangle\\
&\quad=\left\langle\,m\frac{x_{k+1}-x_k}{\varepsilon}\bigl(x_k- x_{k+1}\bigr)\,\right\rangle\\
&\quad=\frac{\hbar}{i}\left\langle\,1\,\right\rangle \tag{7-48}
\end{align}
或いは, これを次のようにも書くことも出来る：
\begin{align}
\left\langle\,m\frac{x_{k+1}-x_k}{\varepsilon}\bigl(x_k-x_{k+1}\bigr)\,\right\rangle
&=\left\langle\,-m\frac{\left(x_{k+1}-x_k\right)^{2}}{\varepsilon}\,\right\rangle\\
&=-m\varepsilon\left\langle\,\left(\frac{x_{k+1}-x_k}{\varepsilon}\right)^{2}\right\rangle
=\frac{\hbar}{i}\left\langle\,1\,\right\rangle\\
\rightarrow\quad \left\langle\,\left(\frac{x_{k+1}-x_k}{\varepsilon}\right)^{2}\right\rangle
&=-\frac{\hbar}{im\varepsilon}\left\langle\,1\,\right\rangle\,\approx \frac{1}{\varepsilon}\quad
\Bigl(\,\rightarrow \infty\quad\mathrm{when}\ \varepsilon\to 0\,\Bigr)
\tag{7-49}
\end{align}
\left\langle\,m\frac{x_{k+1}-x_k}{\varepsilon}\bigl(x_k-x_{k+1}\bigr)\,\right\rangle
&=\left\langle\,-m\frac{\left(x_{k+1}-x_k\right)^{2}}{\varepsilon}\,\right\rangle\\
&=-m\varepsilon\left\langle\,\left(\frac{x_{k+1}-x_k}{\varepsilon}\right)^{2}\right\rangle
=\frac{\hbar}{i}\left\langle\,1\,\right\rangle\\
\rightarrow\quad \left\langle\,\left(\frac{x_{k+1}-x_k}{\varepsilon}\right)^{2}\right\rangle
&=-\frac{\hbar}{im\varepsilon}\left\langle\,1\,\right\rangle\,\approx \frac{1}{\varepsilon}\quad
\Bigl(\,\rightarrow \infty\quad\mathrm{when}\ \varepsilon\to 0\,\Bigr)
\tag{7-49}
\end{align}
この式から,「速度の 2 乗の遷移要素が \(1/\varepsilon\) の程度であり， \(\varepsilon\) がゼロに近づくと無限大に発散すること」が分かる．この結果から, 量子力学的粒子にとって重要な経路というのは,「あらゆる所で確定した勾配(速度)を持つ経路ではなく」, むしろ下図 1.の略図に示したように,「非常に細かいスケールでは極めて不規則な経路である」ということが分かる．実際, このような不規則性は「平均 2 乗速度」が存在しないようなものである．ただし, このときの「平均」という語句は古典的意味での平均 (classical analogue) を指している．ある平均速度が短い時間間隔 \(\Delta t\) で定義されており, 例えば \(\left[x(t+\Delta t)-x(t)\right]/\Delta t\) と定義されているとする．すると上記の結果から, この「平均 2 乗値」は \(-\hbar/(im\Delta t)\) である．すなわち, 短かい時間間隔で平均した速度の「平均 2 乗値」は有限である．しかしながら, その値は時間間隔が短くなるに連れて, どんどん大きくなって行くのである!．
量子力学的経路は非常に不規則なように見える．けれども, 適当な時間間隔で平均をとれば, この不規則性は平均化されて無くなり, 相応な移動 (reasonable drift), すなわち“平均”速度を生ずる．しかし, 短かい時間間隔の場合, 速度のその“平均”値は非常に大きくなってしまうのである!!．
図 1.
上の文章は,「チッターべべーブング (Zitterbewegung )」と言われる電子の運動を述べたものと思われる．それについては, Dirac が自著の「量子力学」の§ 69 の中で述べているので, その部分を以下に抜粋して示しておこう．
上記の理論によって, ハイゼンベルク描像での自由電子の運動を考察し, そしてハイゼンベルクの運動方程式を研究することは興味深い事柄である．これらの運動方程式は正確に積分することが出来る．それはシュレディンガーによって最初に行われた ( Schrödinger, Sitzungsb. d. Berlin. Akad., 1930, p.418 )．§ 28 の表記では, ハイゼンベルク描像において時間とともに変化する力学変数には添字 \(t\) が挿入されたが, ここでは表現を簡潔にするためにそれを省略することにする．
ハミルトニアンとしては, 式 (10) の \(\psi\) に演算子を作用させたときにゼロとなるような \(cp_0\) に等しい表現にしなければならない (As Hamiltonian we must take the expression which we get as equal to \(cp_0\) when we put the operator on \(\psi\) in (10) equal to zero)．すなわち次とする：
\begin{equation}
\def\mb#1{\mathbf{#1}}
H=c\rho_1\mb{\sigma}\cdot\mb{p}+\rho_3\,mc^{2}=c\mb{\alpha}\cdot\mb{p}+\rho_3\,mc^{2}
\tag{69.23}
\end{equation}
( 参考 ) 相対論における \(4\)-元運動量は， \(p^{\mu}=(E/c,\mathbf{p})\) であった．従って系のエネルギーは \(E=cp^{0}\) である．式 (10) に \(c\) を掛け合わせると,
\begin{equation}
\{cp_0-c\rho_1\,\mb{\sigma}\cdot\mb{p} – c\rho_3\,mc\}\psi
=\{cp_0-c\mb{\alpha}\cdot\mb{p}-\rho_3\,mc^{2}\}\psi = 0,
\end{equation}
\{cp_0-c\rho_1\,\mb{\sigma}\cdot\mb{p} – c\rho_3\,mc\}\psi
=\{cp_0-c\mb{\alpha}\cdot\mb{p}-\rho_3\,mc^{2}\}\psi = 0,
\end{equation}
よって \(cp_0\) に等しいハミルトニアン \(H\) としては, 次とすれば良いことになる：
\begin{equation}
cp_0\psi=H\psi=\left(c\rho_1\,\mb{\sigma}\cdot\mb{p} + \rho_3\,mc^{2}\right)\psi
=\left(c\mb{\alpha}\cdot\mb{p}+\rho_3\,mc^{2}\right)\psi=0
\end{equation}
cp_0\psi=H\psi=\left(c\rho_1\,\mb{\sigma}\cdot\mb{p} + \rho_3\,mc^{2}\right)\psi
=\left(c\mb{\alpha}\cdot\mb{p}+\rho_3\,mc^{2}\right)\psi=0
\end{equation}
運動量は \(H\) と交換可能であることはすぐ分かる．従って, 運動量は運動の定数である．さらに, 速度の \(x_1\)-成分は, ハイゼンベルクの運動方程式を用いて次となる：
\begin{equation}
\dot{x}_1=\frac{d x_1}{dt}=[x_1,H]_q=c\alpha_1
\tag{69.24}
\end{equation}
この結果はどちらかと言えば意外なものである．なぜなら, 速度と運動量の関係が, 古典力学におけるものとはまったく異なっていることを意味しているからである．しかしながら, それは確率の流れの成分に対する表現 \(\psi^{\dagger}c\alpha_1\psi\) と関係しているのである．
( 参考 ) ハイゼンベルクの運動方程式 (5.13) は次である：
\begin{equation}
\frac{d x_1}{dt}=\frac{1}{i\hbar}(x_1\,H – H\,x_1)=[x_1, H]_q=\frac{1}{i\hbar}[x_1, H]
\end{equation}
\frac{d x_1}{dt}=\frac{1}{i\hbar}(x_1\,H – H\,x_1)=[x_1, H]_q=\frac{1}{i\hbar}[x_1, H]
\end{equation}
正準座標とその正準運動量の交換関係 \([x_i,p_j]=i\hbar\delta_{ij}\) より,
\begin{align}
[x_1,H]&=x_{1}c\mb{\alpha}\cdot\mb{p}-c\mb{\alpha}\cdot\mb{p}x_{1}
=cx_1(\alpha_1p_1+\alpha_2p_2+\alpha_3p_3)-c(\alpha_1p_1+\alpha_2p_2+\alpha_3p_3)x_1\\
&=c\alpha_1(x_1p_1-p_1x_1)+c\alpha_2(x_1p_2-p_2x_1)+c\alpha_3(x_1p_3-p_3x_1)\\
&=c\alpha_1(x_1p_1-p_1x_1)=c\alpha_1 i\hbar
\end{align}
[x_1,H]&=x_{1}c\mb{\alpha}\cdot\mb{p}-c\mb{\alpha}\cdot\mb{p}x_{1}
=cx_1(\alpha_1p_1+\alpha_2p_2+\alpha_3p_3)-c(\alpha_1p_1+\alpha_2p_2+\alpha_3p_3)x_1\\
&=c\alpha_1(x_1p_1-p_1x_1)+c\alpha_2(x_1p_2-p_2x_1)+c\alpha_3(x_1p_3-p_3x_1)\\
&=c\alpha_1(x_1p_1-p_1x_1)=c\alpha_1 i\hbar
\end{align}
よって, 次となる：
\begin{equation}
v_1=\frac{d x_1}{dt}=\frac{1}{i\hbar}[x_1, H]=\frac{1}{i\hbar} c\alpha_1i\hbar=c\alpha_1
\end{equation}
v_1=\frac{d x_1}{dt}=\frac{1}{i\hbar}[x_1, H]=\frac{1}{i\hbar} c\alpha_1i\hbar=c\alpha_1
\end{equation}
また, 古典力学における速度 \(u^{\mu}\) と運動量 \(p^{\mu}\) は質量 \(m\) として次で与えられる：
\begin{equation}
u^{\mu}=(\gamma c,\gamma\mb{v}),\quad p^{\mu}=m\,u^{\mu}=(\gamma mc,\gamma m\mb{v}),\quad\mathrm{where}\quad \gamma=\frac{1}{\sqrt{1-|\mb{v}|/c}}
\end{equation}
u^{\mu}=(\gamma c,\gamma\mb{v}),\quad p^{\mu}=m\,u^{\mu}=(\gamma mc,\gamma m\mb{v}),\quad\mathrm{where}\quad \gamma=\frac{1}{\sqrt{1-|\mb{v}|/c}}
\end{equation}
また古典力学における密度 \(\rho\) の流体について, その流れを \(\mb{j}=\rho\mb{v}\) とすると次の連続の方程式が成り立つ：
\begin{equation}
\def\ppdiff#1#2{\frac{\partial #1}{\partial #2}}
\ppdiff{\rho}{t}+\mathrm{div}\,\mb{j}=\ppdiff{\rho}{t}+\mathrm{div}(\rho\mb{v})=0
\end{equation}
\def\ppdiff#1#2{\frac{\partial #1}{\partial #2}}
\ppdiff{\rho}{t}+\mathrm{div}\,\mb{j}=\ppdiff{\rho}{t}+\mathrm{div}(\rho\mb{v})=0
\end{equation}
この式とここでの連続の方程式 \(\partial_{\mu}j^{\mu}=0\) とが一致するためには, 確率密度 \(\rho\) と確率の流れ \(j^{\mu}\) を次のように取ればよかった：
\begin{equation}
j^{\mu}=(c\rho,\mb{j}),\quad
\rho=\psi^{\dagger}\psi,\quad \mb{j}=\psi^{\dagger}c\mb{\alpha}\psi=\psi^{\dagger}\mb{v}\psi
\end{equation}
j^{\mu}=(c\rho,\mb{j}),\quad
\rho=\psi^{\dagger}\psi,\quad \mb{j}=\psi^{\dagger}c\mb{\alpha}\psi=\psi^{\dagger}\mb{v}\psi
\end{equation}
すなわち， \(\mb{v}=c\mb{\alpha}\) の関係となっていることが分かる．
式 (69.24) で与えられる \(\dot{x}_1\) は， \(\alpha_1\) の固有値が \(\pm 1\) であることから, 固有値として \(\pm c\) を持つ． \(\dot{x}_2\) と\(\dot{x}_3\) も同様であるから次のように結論することが出来る：「自由電子の速度の成分を測定すると必ず \(\pm c\) となる」．場が存在するときにも, このことが成り立つことは容易に確かめられる．
( 参考 ) 式 (69.24) の両辺を二乗すると， \(\alpha_1^{2}=1\) より次が言える：
\begin{equation}
\dot{x}_1^{2}=c^{2}\alpha_1^{2}=c^{2},\quad\rightarrow \quad
\dot{x}_1^{2}\psi=c^{2}\psi
\end{equation}
\dot{x}_1^{2}=c^{2}\alpha_1^{2}=c^{2},\quad\rightarrow \quad
\dot{x}_1^{2}\psi=c^{2}\psi
\end{equation}
これは \(\dot{x}_1^{2}\) の固有値が \(c^{2}\) であることを示している．従って \(\dot{x}_1\) の固有値は \(\pm c\) であると言える．また, 場が存在する場合は \(\mb{p}\) を \(\displaystyle{\mb{\Pi}\equiv \mb{p}+\frac{e}{c}\mb{A}}\) に置き換えるだけで同じ議論が出来て， 式 (69.24) と全く同じ式 \(\dot{x}_1=c\alpha_1\) を得る．その際 \(\mb{A}(\mb{x})\) は \(\mb{x}\) と可換であることを用いる．
実際に電子の速度を観測すると光速よりも遅いので， ここで実験と矛盾する結論を持ったように思える．しかしその矛盾は実在しない．なぜなら, 上記の結論における理論的速度はある瞬間での速度であるのに対して, 観測される速度は常に感知できるほどの時間間隔の間の平均速度であるからである．運動方程式をさらに調べると, 速度は決して一定ではなくて, 観測値と一致する平均値のあたりで急速に振動していることが分かるのである．
相対論的な理論では速度の成分を測定すると \(\pm c\) とならねばならないことは, 単に § 24 の不確定性原理を初等的に適用することで容易に確かめることが出来る．速度を測定するためには僅かに異なる \(2\) つの時刻での位置を測定し, そのあとその位置変化をその時間間隔で割り算しなければならない．(運動量を測定し公式を当てはめることはうまくいかないであろう．なぜなら速度と運動量間の通常の関係は正しくないからである)．我々が測定した速度が瞬間的な速度の近似値となり得るためには, 位置の \(2\) つの測定間の時間間隔は非常に短いものでなければならない．従ってこれらの測定は非常に正確でなければならない．時間間隔の間の電子位置が非常に正確になると, 不確定性原理によってその運動量はほとんど完全に不確定とならねばならない．これは運動量のほとんど全ての値が同じ確率を持つことを意味する．従って運動量はほとんど確実に無限大である．運動量の成分が無限大の値を持つということは, それに相当する速度成分が値 \(\pm c\) であることになる．
さて今度は, 電子の速度が時間とともにどのように変化するかを調べることにしよう． \(\alpha_1\) について, ハイゼンベルクの運動方程式を考えるならば次が言える：
\begin{equation}
\frac{d\alpha_1}{dt}=\dot{\alpha}_1=\frac{1}{i\hbar}(\alpha_1 H – H \alpha_1)
\end{equation}
さて， \(\alpha_1\) は \(H\) 中の \(c\alpha_1 p_1\) 以外の全ての項と反交換するので， \(\alpha_1\) と \(H\) の反交換関係でゼロとならないのは次だけとなる：
\begin{equation}
\alpha_1 H + H \alpha_1 = \alpha_1 c\alpha_1 p_1 + c\alpha_1 p_1 \alpha_1 = 2c\,p_1
\end{equation}
従って上の \(2\) 式から次が言える：
\begin{align}
i\hbar\dot{\alpha}_1&=\alpha_1 H – H \alpha_1\\
&\downarrow \quad H\alpha_1 = 2c\,p_1-\alpha_1 H\ を代入すると\\
&=\alpha_1 H – (2c\,p_1-\alpha_1 H)=2\alpha_1 H – 2c\,p_1\\
\rightarrow \quad i\hbar\dot{\alpha}_1&=2\alpha_1 H – 2c\,p_1
\tag{69.25a}
\end{align}
または \(\alpha_1 H = 2c\,p_1 – H\alpha_1\) を代入するならば,
\begin{align}
\alpha_1 H – H \alpha_1&=2c\,p_1 – H\alpha_1 – H\alpha_1 = 2c\,p_1 -2H\alpha_1\\
\rightarrow \quad i\hbar\dot{\alpha}_1&=2c\,p_1 -2H\alpha_1
\tag{69.25b}
\end{align}
\(H\) と \(p_1\) は一定であるので, 式 (69.25a) の両辺を時間微分すると次が得られる：
\begin{equation}
i\hbar\ddot{\alpha}_1 = (2\dot{\alpha}_1 H + 2\alpha_1 \dot{H})
-2c \dot{p}_1 = 2\dot{\alpha}_1 H
\tag{69.26}
\end{equation}
この \(\dot{\alpha}_1\) についての微分方程式は, すぐに積分できて結果は次となる：
\begin{equation}
\dot{\alpha}_1=\dot{\alpha}^{0}_{1}\,e^{-2iHt/\hbar}
\tag{69.27}
\end{equation}
ただし \(\dot{\alpha}_1^{0}\) は定数であり， \(t=0\) における \(\dot{\alpha}_1\) の値に等しい．式 (69.26) 中で \(H\) は \(\dot{\alpha}_1\) の右側に現れているため, 式 (69.27) 中における因子 \(e^{-2iHt/\hbar}\) は，(やはり同じ順となるように)因子 \(\dot{\alpha}_1^{0}\) の右側に置かれなければならない．同様にして,式 (69.25b) からは次の結果が得られる：
\begin{equation}
\dot{\alpha}_1=e^{2iHt/\hbar}\,\dot{\alpha}_1^{0}
\end{equation}
すると今や \(x_1\) に対する運動方程式の積分は容易に達成することが出来る．式 (69.27) の \(\dot{\alpha}_1\) を式 (69.25a) に代入すると,
\begin{equation}
i\hbar\dot{\alpha}_1=i\hbar \dot{\alpha}_1^{0}\,e^{-2iHt/\hbar} = 2\alpha_1\,H -2c\,p_1
\end{equation}
この両辺に右から \(1/2H\) を掛け合わせるならば,
\begin{align}
\frac{1}{2}i\hbar&\,\dot{\alpha}_1^{0}\,e^{-2iHt/\hbar}H^{-1} = \alpha_1 – c\,p_1\,H^{-1}\\
\rightarrow &\quad
\alpha_{1}=\frac{1}{2}i\hbar\,\dot{\alpha}_1^{0}\,e^{-2iHt/\hbar}H^{-1}+c\,p_1\,H^{-1}
\tag{69.28}
\end{align}
従って, 式 (69.24) ： \(\dot{x}_1=c\,\alpha_1\) の時間積分は,
\begin{align}
x_1&=\int c\,\alpha_1 dt
=c\int\left(\frac{1}{2}i\hbar\,\dot{\alpha}_1^{0}\,e^{-2iHt/\hbar}H^{-1}
+c\,p_1\,H^{-1}\right)\,dt\\
&=\frac{1}{2}i\hbar\,\dot{\alpha}_1^{0}\,\frac{\hbar}{-2iH}e^{-2iHt/\hbar} H^{-1}+c^{2}p_1H^{-1}t+a_1\\
&=-\frac{1}{4}c\hbar^{2}\dot{\alpha}_1^{0}\,e^{-2iHt/\hbar}H^{-2} + c^{2}p_1 H^{-1}t+a_1
\tag{69.29}
\end{align}
となる．ここで \(a_1\) は積分定数である．
式 (69.28) から, 速度の \(x_1\) 成分 \(c\alpha_1\) は2つの部分からなる事が分かる：
\begin{equation}
\dot{x}_1=c\alpha_1=\frac{1}{2}ic\hbar\,\dot{\alpha}_1^{0}\,e^{-2iHt/\hbar}H^{-1}+c^{2}\,p_1\,H^{-1}
\end{equation}
即ち, 古典的な相対論の公式における運動量と関係する第 2 項の一定部分 \(c^{2}p_1H^{-1}\) と第1項の振動部分,
\begin{equation}
\frac{1}{2}ic\hbar\,\dot{\alpha}_1^{0}\,e^{-2iHt/\hbar}H^{-1}
=\frac{1}{2}ic\hbar\,\dot{\alpha}_1^{0}\,e^{-i\omega t}H^{-1},\quad \omega=2\pi\nu=\frac{2H}{\hbar}
\end{equation}
である．この振動項の振動数は \(\nu=2H/h\) であるが, その最小値は \(\nu_0=2mc^{2}/h\) である．(つまり, 自由電子が静止している場合に持つ静止エネルギー \(H=mc^{2}\) の場合の値である)．速度を実際に測定するときに観測されるのはこの一定部分であろう．そのような測定では， \(\Delta t_0=1/\nu_0=h/2mc^{2}\) よりも長い時間間隔における平均速度が与えられる．\(\dot{x}_1\) の瞬間値が固有値 \(\pm c\) を持つことは, 振動項において確保されている (電子の振動は光速度で行われている) のである．\(x_1\) の振動部分は小さなものである．それは, 式 (69.29) の第1項であるが, 式 (69.28) を用いて次に書ける：
\begin{align}
-\frac{1}{4}c\hbar^{2}\dot{\alpha}_1^{0}\,e^{-2iHt/\hbar}H^{-2}
&=\frac{1}{2}ic\hbar(\frac{1}{2}i\hbar\dot{\alpha}_1^{0}\,e^{-2iHt/\hbar}H^{-1})H^{-1}
=\frac{1}{2}ic\hbar(\alpha_1-c\,p_1 H^{-1})H^{-1}\\
&\sim \frac{c\hbar}{H}=\frac{c\hbar}{mc^{2}}=\frac{\hbar}{mc}
\end{align}
この大きさは \(\hbar/mc\) のオーダーである．なぜなら \((\alpha_1-c\,p_1 H^{-1})\) の大きさのオーダーが \(1\) であるからである．この小刻みな振動は「ジグザグ運動」(zitterbewegung)と呼ばれる．
