問題 7-11 の後の文章を理解するのにだいぶ苦労したので, その部分に補足や式の導出などを付け加えたものを示しておく.

\(\)
\begin{equation}
\def\ppdiff#1#2{\frac{\partial #1}{\partial #2}}
\int_{-\infty}^{\infty}\chi^{*}(x)\frac{\hbar}{i}\ppdiff{\psi(x)}{x}\,dx
= \int_{-\infty}^{\infty}\chi^{*}(p)\,p\,\psi(p)\,\frac{dp}{2\pi\hbar}
\tag{7-81}
\end{equation}
\def\ppdiff#1#2{\frac{\partial #1}{\partial #2}}
\int_{-\infty}^{\infty}\chi^{*}(x)\frac{\hbar}{i}\ppdiff{\psi(x)}{x}\,dx
= \int_{-\infty}^{\infty}\chi^{*}(p)\,p\,\psi(p)\,\frac{dp}{2\pi\hbar}
\tag{7-81}
\end{equation}
この関係式 (7-81) は次のような別の仕方で理解することも出来る. まず次の遷移振幅を考える:
\begin{equation}
\def\pdiff#1{\frac{\partial}{\partial #1}}
\def\ket#1{|#1\rangle}
\def\bra#1{\langle #1 |}
\def\BK#1#2{\langle #1 | #2 \rangle}
\def\BraKet#1#2#3{\langle #1 | #2 | #3 \rangle}
\BraKet{\chi}{1}{\psi}=\int_{-\infty}^{\infty} dx_b \int_{-\infty}^{\infty} dx_a\ \chi^{*}(x_b,t_b)\,
K(x_b,t_b;x_a,t_a)\,\psi(x_a,t_a)
\tag{7-82}
\end{equation}
\def\pdiff#1{\frac{\partial}{\partial #1}}
\def\ket#1{|#1\rangle}
\def\bra#1{\langle #1 |}
\def\BK#1#2{\langle #1 | #2 \rangle}
\def\BraKet#1#2#3{\langle #1 | #2 | #3 \rangle}
\BraKet{\chi}{1}{\psi}=\int_{-\infty}^{\infty} dx_b \int_{-\infty}^{\infty} dx_a\ \chi^{*}(x_b,t_b)\,
K(x_b,t_b;x_a,t_a)\,\psi(x_a,t_a)
\tag{7-82}
\end{equation}
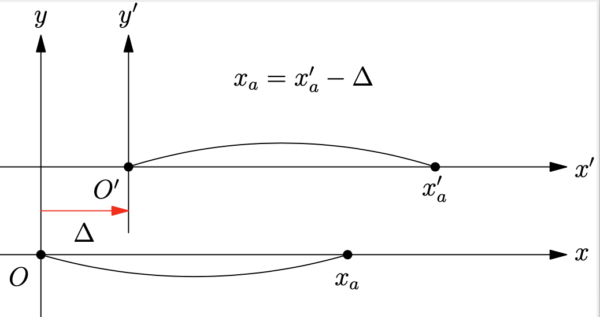
さてここで, 座標軸 \(x_a\) 全体が右に微小量 \(\Delta\) だけ移動したとする ( Now suppose the whole \(x_1\) axis is shifted to the right by a small amount \(\Delta\)). 新しい座標軸を \(x’_a\) と呼ぶと次式が言える (下図 1 を参照):
\begin{equation}
x_a=x’_a-\Delta
\tag{7-83}
\end{equation}
x_a=x’_a-\Delta
\tag{7-83}
\end{equation}
( 注意 ) 校訂版では, 上記の文章が 「Now suppose the \(x_a\) origin is shifted left by a small amount \(\Delta\) .」 つまり和訳すると「座標 \(x_a\) の原点が左に微少量\(\Delta\) だけ移動したとする」と訂正されている. しかし, 下図 1 のように座標をシフトすると考えるならば 原書の表現のままで良いと思われたので, その訂正は採用しないことにしたので注意する.新和訳本の訳も原書の表現のままである.
元の \(x_a\) でなくこの新しい変数 \(x’_a\) を用いても, 式 (7-82) の遷移振幅が変化することはないであろう.
[ なぜなら \(x_a\) の積分範囲は \([-\infty,\infty]\) であるから, 変数変換 \(x_a\to x’_a-\Delta\) を行っても積分範囲は変わらないからである ].
【 わざと座標軸 \(x_a\) を微小量 \(\Delta\) だけ変化させ, そのときの \(\langle | \chi | 1 |\psi\rangle\) の変化量を調べて見るのである.その際に, 問題 2-4 で考えた「端点 \(x_a\) での運動量変化が式 (2-11):\(p=-\partial S/x_a\) で表されることを利用しようという訳である 】.
すると, 式 (7-82) は次となる:
\begin{align}
\BraKet{\chi}{1}{\psi}&=\int dx_b\,\chi^{*}(x_b)\int dx_a\,\psi(x_a)\int_{x_a}^{x_b}
\mathscr{D}x(t)e^{iS[b,a]/\hbar}\notag\\
&\cong\int dx_b\,\chi^{*}(x_b)\int dx’_a\,\psi(x’_a)\int_{x’_a}^{x_b} \mathscr{D}x(t)e^{iS[b,a’]/\hbar}\notag\\
&=\int_{-\infty}^{\infty}dx_b\int_{-\infty}^{\infty}dx’_a\,\int_{x’_a}^{x_N}
\mathscr{D}x(t)\,\chi^{*}(x_N,t_N)\,\exp\Bigg\{\left(\frac{i}{\hbar}\right)\sum_{k=2}^{N-1}
S[x_{k+1},t_{k+1};x_k,t_k]\notag\\
&\qquad+\left(\frac{i}{\hbar}\right)S[x_2,t_2;x’_a-\Delta,t]\Bigg\}\,\psi(x’_a-\Delta,t)
\label{eqn:7.84}
\end{align}
\BraKet{\chi}{1}{\psi}&=\int dx_b\,\chi^{*}(x_b)\int dx_a\,\psi(x_a)\int_{x_a}^{x_b}
\mathscr{D}x(t)e^{iS[b,a]/\hbar}\notag\\
&\cong\int dx_b\,\chi^{*}(x_b)\int dx’_a\,\psi(x’_a)\int_{x’_a}^{x_b} \mathscr{D}x(t)e^{iS[b,a’]/\hbar}\notag\\
&=\int_{-\infty}^{\infty}dx_b\int_{-\infty}^{\infty}dx’_a\,\int_{x’_a}^{x_N}
\mathscr{D}x(t)\,\chi^{*}(x_N,t_N)\,\exp\Bigg\{\left(\frac{i}{\hbar}\right)\sum_{k=2}^{N-1}
S[x_{k+1},t_{k+1};x_k,t_k]\notag\\
&\qquad+\left(\frac{i}{\hbar}\right)S[x_2,t_2;x’_a-\Delta,t]\Bigg\}\,\psi(x’_a-\Delta,t)
\label{eqn:7.84}
\end{align}
ただし, 核の経路積分は 式 (2-29) の方法を用いて明示的に詳述した [ where the path integral for the kernel has been written out explicitly, using the methods of Eq.(2-22) ].
式 (2-29) は次である:
\begin{equation}
K(b,a)=\int \mathscr{D}x(t)\,\exp\left\{\frac{i}{\hbar}S[b,a]\right\}
=\int \mathscr{D}x(t)\,\exp\left[\frac{i}{\hbar}\Bigl\{S[b,c]+S[c,a]\Bigr\}\right]
\end{equation}
K(b,a)=\int \mathscr{D}x(t)\,\exp\left\{\frac{i}{\hbar}S[b,a]\right\}
=\int \mathscr{D}x(t)\,\exp\left[\frac{i}{\hbar}\Bigl\{S[b,c]+S[c,a]\Bigr\}\right]
\end{equation}
( 注意 ) 本文では「式 (2-22) の方法を用いて」と記してあるが, 式(2-29)の方がより直接的であると思われたのでそのように書き換えてある.
この式を利用すると, \(K(b,a)\) すなわち \(K(N,1)\) は次のように表わせることに注意する:
\begin{align}
K(b,a)&\equiv K(x_N,t_N;x_1,t_1)=\int\mathscr{D}x(t)\,\exp\left\{\frac{i}{\hbar}S[N,1]\right\}\\
&=\int \mathscr{D}x(t)\,\exp\left[\frac{i}{\hbar}\Bigl\{S[N,N-1]+\dotsb+S[2,1]\Bigr\}\right]\\
&=\int \mathscr{D}x(t)\,\exp\left[\frac{i}{\hbar}\left\{\sum_{k=1}^{N-1}S\bigl[k+1,k\bigr]\right\}\right]\\
&=\int_{x_1}^{x_N} \mathscr{D}x(t)\,\exp\left[\frac{i}{\hbar}\left\{\sum_{k=2}^{N-1}S\bigl[k+1,k\bigr]\right\}+\frac{i}{\hbar}S[2,1]\right]
\end{align}
K(b,a)&\equiv K(x_N,t_N;x_1,t_1)=\int\mathscr{D}x(t)\,\exp\left\{\frac{i}{\hbar}S[N,1]\right\}\\
&=\int \mathscr{D}x(t)\,\exp\left[\frac{i}{\hbar}\Bigl\{S[N,N-1]+\dotsb+S[2,1]\Bigr\}\right]\\
&=\int \mathscr{D}x(t)\,\exp\left[\frac{i}{\hbar}\left\{\sum_{k=1}^{N-1}S\bigl[k+1,k\bigr]\right\}\right]\\
&=\int_{x_1}^{x_N} \mathscr{D}x(t)\,\exp\left[\frac{i}{\hbar}\left\{\sum_{k=2}^{N-1}S\bigl[k+1,k\bigr]\right\}+\frac{i}{\hbar}S[2,1]\right]
\end{align}
次に \(S[x_2,t_2;x’_a-\Delta,t]\) と \(\psi(x’_a-\Delta,t)\) をテイラー展開し 一次の項のみを残す.近似の式は,
\begin{equation}
f(x-h)\cong f(x)-h\ppdiff{f}{x},\qquad
\ppdiff{e^{iS/\hbar}}{x}=\ppdiff{e^{iS/\hbar}}{S}\ppdiff{S}{x}=\frac{i}{\hbar}e^{iS/\hbar}\ppdiff{S}{x},
\end{equation}
f(x-h)\cong f(x)-h\ppdiff{f}{x},\qquad
\ppdiff{e^{iS/\hbar}}{x}=\ppdiff{e^{iS/\hbar}}{S}\ppdiff{S}{x}=\frac{i}{\hbar}e^{iS/\hbar}\ppdiff{S}{x},
\end{equation}
となるので,
\begin{align}
\psi(x’_a-\Delta,t)&\cong \psi(x’_a,t)-\Delta \ppdiff{\psi(x’_a,t)}{x’_a},\\
\exp\left\{\frac{i}{\hbar}S[x_2,x’_a-\Delta]\right\}&\cong e^{iS/\hbar}-\Delta \ppdiff{e^{iS/\hbar}}{x’_a}\\
&=e^{iS/\hbar}-\Delta\frac{i}{\hbar}e^{iS/\hbar}\ppdiff{S}{x’_a}\\
&=\exp\left\{\frac{i}{\hbar}S[2,1]\right\}\left(1-\frac{i}{\hbar}\Delta\ppdiff{S}{x’_a}\right)\\
\end{align}
\psi(x’_a-\Delta,t)&\cong \psi(x’_a,t)-\Delta \ppdiff{\psi(x’_a,t)}{x’_a},\\
\exp\left\{\frac{i}{\hbar}S[x_2,x’_a-\Delta]\right\}&\cong e^{iS/\hbar}-\Delta \ppdiff{e^{iS/\hbar}}{x’_a}\\
&=e^{iS/\hbar}-\Delta\frac{i}{\hbar}e^{iS/\hbar}\ppdiff{S}{x’_a}\\
&=\exp\left\{\frac{i}{\hbar}S[2,1]\right\}\left(1-\frac{i}{\hbar}\Delta\ppdiff{S}{x’_a}\right)\\
\end{align}
すると, 指数関数は次のようになる:
\begin{align}
&\exp\left\{\frac{i}{\hbar}\sum_{k=1}^{N-1}S[x_{k+1},t_{k+1}; x_k,t_k]\right\}\\
&=\exp\left\{\frac{i}{\hbar}\sum_{k=2}^{N-1}S[x_{k+1},t_{k+1};x_k,t_k]\right\}
\exp\left\{\frac{i}{\hbar}S[x_2,t_2;x’_a-\Delta,t]\right\}\\
&\cong \exp\left\{\frac{i}{\hbar}\sum_{k=2}^{N-1}S[x_{k+1},t_{k+1}; x_k,t_k]\right\}
\exp\left\{\frac{i}{\hbar}S[2,1]\right\}\left(1-\Delta\frac{i}{\hbar}\pdiff{x’_a} S[x_2,t_2;x’_a,t]\right)\\
&=\exp\left\{\frac{i}{\hbar}\sum_{k=2}^{N-1}S[x_{k+1},t_{k+1}; x_k,t_k]+\frac{i}{\hbar}S[2,1]\right\}
\left(1-\Delta\frac{i}{\hbar}\pdiff{x’_a} S[x_2,t_2;x’_a,t]\right)\\
&=\exp\left\{\frac{i}{\hbar}\sum_{k=1}^{N-1}S[x_{k+1},t_{k+1}; x_k,t_k]\right\}
\left(1-\Delta\frac{i}{\hbar}\ppdiff{S[x_2,t_2;x’_a,t]}{x’_a}\right)
\tag{7-85}
\end{align}
&\exp\left\{\frac{i}{\hbar}\sum_{k=1}^{N-1}S[x_{k+1},t_{k+1}; x_k,t_k]\right\}\\
&=\exp\left\{\frac{i}{\hbar}\sum_{k=2}^{N-1}S[x_{k+1},t_{k+1};x_k,t_k]\right\}
\exp\left\{\frac{i}{\hbar}S[x_2,t_2;x’_a-\Delta,t]\right\}\\
&\cong \exp\left\{\frac{i}{\hbar}\sum_{k=2}^{N-1}S[x_{k+1},t_{k+1}; x_k,t_k]\right\}
\exp\left\{\frac{i}{\hbar}S[2,1]\right\}\left(1-\Delta\frac{i}{\hbar}\pdiff{x’_a} S[x_2,t_2;x’_a,t]\right)\\
&=\exp\left\{\frac{i}{\hbar}\sum_{k=2}^{N-1}S[x_{k+1},t_{k+1}; x_k,t_k]+\frac{i}{\hbar}S[2,1]\right\}
\left(1-\Delta\frac{i}{\hbar}\pdiff{x’_a} S[x_2,t_2;x’_a,t]\right)\\
&=\exp\left\{\frac{i}{\hbar}\sum_{k=1}^{N-1}S[x_{k+1},t_{k+1}; x_k,t_k]\right\}
\left(1-\Delta\frac{i}{\hbar}\ppdiff{S[x_2,t_2;x’_a,t]}{x’_a}\right)
\tag{7-85}
\end{align}
遷移振幅を定義する積分でのダッシュ記号は外してよい.なぜなら, \(x’_a\) は積分変数であり, しかも積分範囲が \([-\infty,\infty]\) だからである. そこで, 式 (7-84) の形を \(\Delta\) の一次まで近似すると,
\begin{align}
&\BraKet{\chi}{1}{\psi}_{\Delta}\\
&\cong \int_{-\infty}^{\infty}dx_b\int_{-\infty}^{\infty}dx_a\,\int_{x_a}^{x_N}
\mathscr{D}x(t)\,\chi^{*}(x_b,t_b)\,\exp\Biggl\{\left(\frac{i}{\hbar}\right)\sum_{k=1}^{N-1}S[x_{k+1},t_{k+1};x_k,t_k]\Biggr\}\\
&\quad\times\left(1-\frac{i}{\hbar}\Delta\ppdiff{S}{x_a}\right)\left(\psi(x_a,t_a)
-\Delta\ppdiff{\psi(x_a,t_a)}{x_a}\right)\\
&\cong \int_{-\infty}^{\infty}dx_b\int_{-\infty}^{\infty}dx_a\,\int_{x_a}^{x_b}
\mathscr{D}x(t)\,\chi^{*}(x_b,t_b)\,e^{iS[b,a]/\hbar}\left(\psi(x_a)-\frac{i}{\hbar}\Delta\ppdiff{S}{x_a}
\psi(x_a)-\Delta\ppdiff{\psi}{x_a}\right)\\
&=\int_{-\infty}^{\infty}dx_b\int_{-\infty}^{\infty}dx_a\,\int_{x_a}^{x_b}
\mathscr{D}x(t)\,\chi^{*}(x_b,t_b)\,e^{iS[b,a]/\hbar}\left\{1-\Delta\frac{i}{\hbar}\left(\ppdiff{S}{x_a}
+\frac{\hbar}{i}\pdiff{x_a}\right)\right\}\psi(x_a,t_a)\\
&=\int_{-\infty}^{\infty}dx_b\int_{-\infty}^{\infty}dx_a\,\int_{x_a}^{x_b}
\mathscr{D}x(t)\,\chi^{*}(x_b,t_b)\,e^{iS[b,a]/\hbar}\psi(x_a,t_a)\\
&\quad -\Delta\frac{i}{\hbar}\int_{-\infty}^{\infty}dx_b\int_{-\infty}^{\infty}dx_a\,\int_{x_a}^{x_b}
\mathscr{D}x(t)\,\chi^{*}(x_b,t_b)\,e^{iS[b,a]/\hbar}\left(\ppdiff{S}{x_a}+\frac{\hbar}{i}\pdiff{x_a}\right)
\psi(x_a,t_a)
\end{align}
&\BraKet{\chi}{1}{\psi}_{\Delta}\\
&\cong \int_{-\infty}^{\infty}dx_b\int_{-\infty}^{\infty}dx_a\,\int_{x_a}^{x_N}
\mathscr{D}x(t)\,\chi^{*}(x_b,t_b)\,\exp\Biggl\{\left(\frac{i}{\hbar}\right)\sum_{k=1}^{N-1}S[x_{k+1},t_{k+1};x_k,t_k]\Biggr\}\\
&\quad\times\left(1-\frac{i}{\hbar}\Delta\ppdiff{S}{x_a}\right)\left(\psi(x_a,t_a)
-\Delta\ppdiff{\psi(x_a,t_a)}{x_a}\right)\\
&\cong \int_{-\infty}^{\infty}dx_b\int_{-\infty}^{\infty}dx_a\,\int_{x_a}^{x_b}
\mathscr{D}x(t)\,\chi^{*}(x_b,t_b)\,e^{iS[b,a]/\hbar}\left(\psi(x_a)-\frac{i}{\hbar}\Delta\ppdiff{S}{x_a}
\psi(x_a)-\Delta\ppdiff{\psi}{x_a}\right)\\
&=\int_{-\infty}^{\infty}dx_b\int_{-\infty}^{\infty}dx_a\,\int_{x_a}^{x_b}
\mathscr{D}x(t)\,\chi^{*}(x_b,t_b)\,e^{iS[b,a]/\hbar}\left\{1-\Delta\frac{i}{\hbar}\left(\ppdiff{S}{x_a}
+\frac{\hbar}{i}\pdiff{x_a}\right)\right\}\psi(x_a,t_a)\\
&=\int_{-\infty}^{\infty}dx_b\int_{-\infty}^{\infty}dx_a\,\int_{x_a}^{x_b}
\mathscr{D}x(t)\,\chi^{*}(x_b,t_b)\,e^{iS[b,a]/\hbar}\psi(x_a,t_a)\\
&\quad -\Delta\frac{i}{\hbar}\int_{-\infty}^{\infty}dx_b\int_{-\infty}^{\infty}dx_a\,\int_{x_a}^{x_b}
\mathscr{D}x(t)\,\chi^{*}(x_b,t_b)\,e^{iS[b,a]/\hbar}\left(\ppdiff{S}{x_a}+\frac{\hbar}{i}\pdiff{x_a}\right)
\psi(x_a,t_a)
\end{align}
従って,
\begin{align}
&\BraKet{\chi}{1}{\psi}_{\Delta}=\int_{-\infty}^{\infty} dx_b\int_{-\infty}^{\infty} dx_a\,\chi^{*}(b)K(b,a)\psi(a)\\
&\quad -\Delta\frac{i}{\hbar}
\int_{-\infty}^{\infty} dx_b\int_{-\infty}^{\infty} dx_a\,\chi^{*}(b)K(b,a)
\Bigg\{\ppdiff{S[x_2,t_2;x_a,t_a]}{x_a}\psi(x_a,t_a)+\frac{\hbar}{i}\ppdiff{\psi(x_a,t_a)}{x_a}\Bigg\}
\tag{7-86}
\end{align}
&\BraKet{\chi}{1}{\psi}_{\Delta}=\int_{-\infty}^{\infty} dx_b\int_{-\infty}^{\infty} dx_a\,\chi^{*}(b)K(b,a)\psi(a)\\
&\quad -\Delta\frac{i}{\hbar}
\int_{-\infty}^{\infty} dx_b\int_{-\infty}^{\infty} dx_a\,\chi^{*}(b)K(b,a)
\Bigg\{\ppdiff{S[x_2,t_2;x_a,t_a]}{x_a}\psi(x_a,t_a)+\frac{\hbar}{i}\ppdiff{\psi(x_a,t_a)}{x_a}\Bigg\}
\tag{7-86}
\end{align}
よって,
\begin{align}
&\BraKet{\chi}{1}{\psi}_{\Delta}=\BraKet{\chi}{1}{\psi}\\
&=\BraKet{\chi}{1}{\psi} -\Delta \frac{i}{\hbar}\int_{-\infty}^{\infty} dx_b\int_{-\infty}^{\infty} dx_a\,
\chi^{*}(x_b)\,K(b,a)\left\{\ppdiff{S}{x_a}\psi(x_a)+\frac{\hbar}{i}\ppdiff{\psi}{x_a}\right\}
\tag{7.86′}
\end{align}
&\BraKet{\chi}{1}{\psi}_{\Delta}=\BraKet{\chi}{1}{\psi}\\
&=\BraKet{\chi}{1}{\psi} -\Delta \frac{i}{\hbar}\int_{-\infty}^{\infty} dx_b\int_{-\infty}^{\infty} dx_a\,
\chi^{*}(x_b)\,K(b,a)\left\{\ppdiff{S}{x_a}\psi(x_a)+\frac{\hbar}{i}\ppdiff{\psi}{x_a}\right\}
\tag{7.86′}
\end{align}
ただし, これまでの表記を保持することとし, 点 \(x_2\) は経路 \(x(t)\) 上で \(x_a=x_1\) とほんの僅かの時間間隔 \(\varepsilon\) だけ離れているとする.従って \(t_2=t_a+\varepsilon\) である.
以上の結果式 (7-86′) を見ると, その右辺の第 1 項は 左辺の遷移振幅と等しい.よって, その右辺の残りの項はゼロでなければならない.しかし, この残りの項は 2つの遷移要素の組み合わせである:
\begin{align}
&\int_{-\infty}^{\infty} dx_b\int_{-\infty}^{\infty} dx_a\,\chi^{*}(x_b)\,K(b,a)\left\{\ppdiff{S}{x_a}\psi(x_a)
+\frac{\hbar}{i}\ppdiff{\psi}{x_a}\right\}\\
&=\int_{-\infty}^{\infty} dx_b\int_{-\infty}^{\infty} dx_a\,\chi^{*}(x_b)\int_{a}^{b}\mathscr{D}x(t)\,e^{iS/\hbar}
\left\{\ppdiff{S}{x_a}\psi(x_a)+\frac{\hbar}{i}\pdiff{x_a}\psi(x_a)\right\}\\
&=\int dx_b\int dx_a\,\chi^{*}(x_b)\int_{a}^{b}\mathscr{D}x(t)\,e^{iS/\hbar}\ppdiff{S}{x_a}\psi(x_a)
+\int dx_b\int dx_a\,\chi^{*}(x_b)\int_{a}^{b}\mathscr{D}x(t)\,e^{iS/\hbar}\frac{\hbar}{i}\pdiff{x_a}
\psi(x_a)\\
&=\left\langle\chi\left|\ppdiff{S}{x_a}\right|\psi\right\rangle+\left\langle\chi\left|\frac{\hbar}{i}
\pdiff{x_a}\right|\psi\right\rangle=0,\quad\rightarrow\quad
-\left\langle\chi\left|\ppdiff{S}{x_a}\right|\psi\right\rangle=\left\langle\chi\left|\frac{\hbar}{i}
\pdiff{x_a}\right|\psi\right\rangle
\end{align}
&\int_{-\infty}^{\infty} dx_b\int_{-\infty}^{\infty} dx_a\,\chi^{*}(x_b)\,K(b,a)\left\{\ppdiff{S}{x_a}\psi(x_a)
+\frac{\hbar}{i}\ppdiff{\psi}{x_a}\right\}\\
&=\int_{-\infty}^{\infty} dx_b\int_{-\infty}^{\infty} dx_a\,\chi^{*}(x_b)\int_{a}^{b}\mathscr{D}x(t)\,e^{iS/\hbar}
\left\{\ppdiff{S}{x_a}\psi(x_a)+\frac{\hbar}{i}\pdiff{x_a}\psi(x_a)\right\}\\
&=\int dx_b\int dx_a\,\chi^{*}(x_b)\int_{a}^{b}\mathscr{D}x(t)\,e^{iS/\hbar}\ppdiff{S}{x_a}\psi(x_a)
+\int dx_b\int dx_a\,\chi^{*}(x_b)\int_{a}^{b}\mathscr{D}x(t)\,e^{iS/\hbar}\frac{\hbar}{i}\pdiff{x_a}
\psi(x_a)\\
&=\left\langle\chi\left|\ppdiff{S}{x_a}\right|\psi\right\rangle+\left\langle\chi\left|\frac{\hbar}{i}
\pdiff{x_a}\right|\psi\right\rangle=0,\quad\rightarrow\quad
-\left\langle\chi\left|\ppdiff{S}{x_a}\right|\psi\right\rangle=\left\langle\chi\left|\frac{\hbar}{i}
\pdiff{x_a}\right|\psi\right\rangle
\end{align}
従って,
\begin{equation}
\left\langle \chi\left|\,-\ppdiff{S[x_2,t_2\,; x_a,t_a]}{x_a}\,\right|\psi\right\rangle
=\left\langle \chi\Biggl|\,1\,\Biggr|\frac{\hbar}{i}\ppdiff{\psi(x_a,t_a)}{x_a}\,\right\rangle
\tag{7-87}
\end{equation}
\left\langle \chi\left|\,-\ppdiff{S[x_2,t_2\,; x_a,t_a]}{x_a}\,\right|\psi\right\rangle
=\left\langle \chi\Biggl|\,1\,\Biggr|\frac{\hbar}{i}\ppdiff{\psi(x_a,t_a)}{x_a}\,\right\rangle
\tag{7-87}
\end{equation}
式 (2-22) の取り決めでは, 経路の短い要素に沿った古典的作用を用いていた.従って, 式 (7-87) に現れる作用 \(S[b,a]\) は初期の経路要素に相当する古典的作用 \(S_{cl}\) である.
作用 \(S\) の \(x_a\) についての導関数に負号を付けたものは「初期位置 \(x_a\) に於ける運動量の古典力学的定義 」である.従って, 次のように表わす:
\begin{equation}
\BraKet{\chi}{p_a}{\psi}=\left\langle \chi\Biggl|\,1\,\Biggr|\frac{\hbar}{i}\ppdiff{\psi(x_a,t_a)}{x_a}\,\right\rangle
\tag{7-88}
\end{equation}
\BraKet{\chi}{p_a}{\psi}=\left\langle \chi\Biggl|\,1\,\Biggr|\frac{\hbar}{i}\ppdiff{\psi(x_a,t_a)}{x_a}\,\right\rangle
\tag{7-88}
\end{equation}
これは式 (7-78) と式 (7-79) で得られた結果と同じである.
恐らく相互作用部分を部分消去すると, ときどき \(S\) が複雑な式となってしまう.その複雑な \(S\) を扱う場合には, 時刻 \(t\) の運動量に相当する汎関数 \(p(t)\) を特定したくなる.そのとき, 前段で述べた議論が, 一般的な定義をする際の示唆となる.時間 \(t\) より前の時刻に相当する座標の全てが \(-\Delta\) だけシフトした場合, 式 (7-86) \(\sim\) 式 (7-88) より, 遷移振幅 \(\BraKet{\chi}{1}{\psi}\) の 1次変化は, およそ \(\BraKet{\chi}{p(t)}{\psi}\) に \((-i/\hbar)\Delta\) を掛け合わせたものとなる.
この原理から, 運動量汎関数は, 作用 \(S\) がどんな複雑な場合であっても見出すことが出来るであろう.同様にして, ハミルトニアン即ちエネルギーは「時間変数をシフトすること」により定義できる.このことは § 7.7 で述べるであろう.
【 メモ 】 (1) 式 (7-87) の下の文章は, 問題 2-4 に於ける式 (2-10) と式 (2-11) とから言えることである:
\begin{align}
p=\ppdiff{L}{\dot{x}},\qquad\left(\ppdiff{L}{\dot{x}}\right)_{x=x_a}=-\ppdiff{S_{cl}}{x_a},
\qquad\rightarrow \qquad p(x_a)=-\ppdiff{S_{cl}}{x_a}
\end{align}
p=\ppdiff{L}{\dot{x}},\qquad\left(\ppdiff{L}{\dot{x}}\right)_{x=x_a}=-\ppdiff{S_{cl}}{x_a},
\qquad\rightarrow \qquad p(x_a)=-\ppdiff{S_{cl}}{x_a}
\end{align}
古典解析力学では,「一般化運動量」の作用による定義は \(p_i=\partial S/\partial q_i\) である (ランダウ:「力学」の § 31 を参照のこと).式 (7-87) の場合は, 問題 2-4 にあるように下限 \(t_a\) での運動量を考えるのでマイナス符号が付くのである.
(2) 式 (7-88) 以降の議論はオーダーでの話であろう.また, 原書では「\(\Delta\) を掛け合わせたものとなる」となっているが,「\((-i/\hbar)\Delta\) 」であると思われたので, 修正して書いておくことにする.
\begin{equation}
\BraKet{\chi}{1}{\psi}_{\Delta}\quad\sim\quad\BraKet{\chi}{1}{\psi}\ – \ \Delta \frac{i}{\hbar}\BraKet{\chi}{p}{\psi}
\end{equation}
\BraKet{\chi}{1}{\psi}_{\Delta}\quad\sim\quad\BraKet{\chi}{1}{\psi}\ – \ \Delta \frac{i}{\hbar}\BraKet{\chi}{p}{\psi}
\end{equation}