\(\)
問題 8-3 へ回答するための準備として,「1の累乗根」についてまとめておこう．自分で説明文を書く自信がないので, 次のウェブサイト記事の一部を訳すことで(多少の補足を加えて), まとめに代えることにする：
https://people.math.carleton.ca/~ckfong/C2.pdf
1の累乗根
正の整数 \(n\) が与えられたとき, 複素数 \(z\) が \(z^{n}＝1\) を満たすならば, この \(z\) を \(1\) の \(n\) 乗根 ( \(n\)th root of unity ) と呼ぶ．言い換えれば, \(z\) は多項式 \(X^{n} – 1\) の根である．複素数 \(e^{i2\pi/n}\) を \(\omega_n\) で, または \(n\) が分かっているならば単に \(\omega\) で表わす：
\omega\equiv \omega_n = e^{i2\pi/n} \equiv \cos \frac{2\pi}{n} + i\sin\frac{2\pi}{n}
\tag{1}
\end{equation}
このとき \(\omega^{n}=(e^{i2\pi/n})^{n}=e^{i2\pi}=1\) なので, \(\omega\) は \(1\) の \(n\)乗根であることが分かる．次の複素数
1,\quad \omega,\quad \omega^{2},\ \dotsb,\quad \omega^{n-1},
\tag{2}
\end{equation}
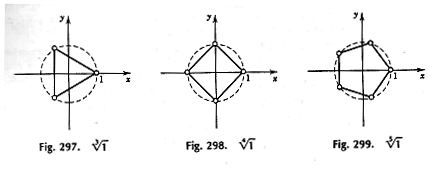
を複素平面上の点と見なすと, これらは単位円に内接する正 \(n\) 角形の頂点となる．例えば, \(n=3\), \(n=4\), \(n=5\) の場合は, 図 1 のような頂点となる．
図 1. E. Kreyszig : Advanced Engineering Mathematics に依る．
\(1,\,\omega,\,\omega^{2},\,\dotsb,\,\omega^{n-1}\) のこの特殊な幾何学的配置のために, それらの合計がゼロになると考えるのは難しいことではない：
\[ 1+\omega+\omega^{2}+\dotsb+\omega^{n-1}=0.\tag{3}\]
この非常に重要な恒等式を代数的に証明して見よう．\(\omega^{n} = 1\) から, 次となる：
(1-\omega)(1+\omega+\omega^{2}+\dotsb+\omega^{n-1})=1-\omega^{n}=0.
\tag{4}
\end{equation}
明らかに \(\omega\ne 1\), つまり \(1-\omega\ne0\) である．従って式 (3) が言える．
\(\omega,\,\omega^{2},\,\dotsb,\,\omega^{n-1}\) の各々は \(1\) の \(n\)乗根である．実際, \(0\le k \le n-1\) として \(z=\omega^{k}\) とすると,
z^{n}=\left(\omega^{k}\right)^{n}=\left(\omega^{n}\right)^{k}=1^{k}=1.
\tag{5}
\end{equation}
従って, \(1,\,\omega,\,\omega^{2},\,\dotsb,\,\omega^{n-1}\) は \(X^{n}-1\) のちょうど \(n\) 個の異なる根である．各根 \(\omega^{k}\) は \(X^{n} -1\) の1次因子 \(X -\omega^{k}\) に寄与する．従って, \(X^{n} -1\) の因数分解は次のようになる：
X^{n} -1=(X-1)(X-\omega)(X-\omega^{2})\dotsb(X-\omega^{n-1})=\prod_{k=0}^{n-1}\big(X-\omega^{k}\big).
\tag{6}
\end{equation}
この最後の表現は, \(X-\omega^{k}\) (\(k\) は \(0\) から \(n-1\) まで) の積と読むことが出来る．
恒等式 (3) からは, 各根 \(\omega^{k}=e^{i2\pi k/n}\) の直交性が言える．式 (5) から, \(\omega^{k}\) についても式 (4) と同様な式が成り立つは明らかだ：
\big(1-\omega^{kn}\big)=\bigl(1-\omega^{k}\bigr)\bigl(1+\omega^{k}+\omega^{2k}+\dotsb+\omega^{k(n-1)}\bigr)=0
\tag{7}
\end{equation}
明らかに \(\omega^{k}\ne0\), つまり \(1-\omega^{k}\ne0\) であるから,
1+\omega^{k}+\omega^{2k}+\dotsb+\omega^{k(n-1)}=0,\quad k\ne 0
\tag{8}
\end{equation}
従って, \(k\ne0\) の場合, 次が言える：
\sum_{m=0}^{n-1} \omega^{km}=\sum_{m=0}^{n-1} \exp\left(i\frac{2\pi}{n}k\,m\right)=0
\tag{9}
\end{equation}
\(k=0\) の場合は明らかに次が言える：
\sum_{m=0}^{n-1} \omega^{km}=\sum_{m=0}^{n-1} 1 = 1+1+\dotsb +1 = 1\times n =n
\tag{10}
\end{equation}
以上のことを次のように言い換える．\(a,\,b\) をゼロでない整数として \(k=a-b\) とおく．すると,
\sum_{m=0}^{n-1} \omega^{km}=\sum_{m=0}^{n-1} \omega^{(a-b)m}=\sum_{m=0}^{n-1} \exp\left\{ i\frac{2\pi}{n}(a-b)m \right\}
\tag{11}
\end{equation}
従って, 式 (9) と式 (10) とはまとめて次のように書くことが出来る：
\[\sum_{m=0}^{n-1} \exp\left\{ i\frac{2\pi}{n}(a-b)m \right\}=\sum_{m=0}^{n-1} \exp\left(i\frac{2\pi}{n}a\,m\right)\exp\left(-i\frac{2\pi}{n}b\,m\right)
=\begin{cases}
0 & a\ne b \\
n & a=b
\end{cases}
\tag{12}
\]
これは関数 \(\omega^{k}=e^{i2\pi k/n}\) の直交性を表している．または, 上式を \(n\) で割り算すれば, 次のような「規格直交性」を表した式となる：
\[\frac{1}{n}\sum_{m=0}^{n-1} \exp\left\{ i\frac{2\pi}{n}(a-b)m \right\}=\sum_{m=0}^{n-1} \frac{1}{\sqrt{n}}\exp\left(i\frac{2\pi}{n}a\,m\right)\frac{1}{\sqrt{n}}\exp\left(-i\frac{2\pi}{n}b\,m\right)=\delta_{a\,b}\tag{13}\]
