\(\)
調和振動子の標準的な量子力学教科書の記述として, L.Pauling & B.Wilson の Introduction to Quantum Mechanics with Applications to chemistry 第11章 を抜粋して示すことにする.
11. THE HARMONIC OSCILLATOR IN WAVE MECHANICS
11a. 波動方程式の解法
力学系に対する最初のシュレディンガー波動方程式の解法例として, 1次元の調和振動子を選ぶことにする.それは波動方程式に適用する解法についての良い説明となるだけでなく,この系は後に議論する応用, 例えば分子の振動エネルギーの計算など, に於いて大変重要だからである.より困難な3次元振動子の問題は, 古典力学的な方法での取り扱いを §1a. で行った.他方, 簡単な1次元の場合は, 古い量子論による議論を §6a. で行った.
前と同様に, ポテンシャルエネルギーは \(V(x)=2\pi^{2}m\nu_0^{2}x^{2}\) の形に書くことが出来る.ただし \(x\) は質量 \(m\) の粒子の平衡位置 \(x=0\) からの変位である.これを1次元系の一般的な波動方程式 (9-8): \(\displaystyle{\frac{d^{2}\psi}{dx^{2}}+\frac{8\pi^{2}m}{h^{2}}\big(W-V(x)\big)\psi =0}\) に代入すると,
\frac{d^{2}\psi}{dx^{2}}+\frac{8\pi^{2}m}{h^{2}}\big(W-2\pi^{2}m\nu_0^{2}x^{2}\big)\psi =0
\tag{11.1}
\end{equation}
または, 便宜のために量 \(\lambda = 8\pi^{2}mW/h^{2}\)と\(\alpha=4\pi^{2}m\nu_0/h\) を導入すると次となる:
\frac{d^{2}\psi}{dx^{2}} + \big(\lambda-\alpha^{2}x^{2}\big)\psi = 0
\tag{11.2}
\end{equation}
\(x\) の値が \(-\infty\) から \(\infty\) の全領域に於いて, 関数 \(\psi(x)\) はこの方程式を満足すること, また, この全領域で望ましい関数である, すなわち一価で有限な連続関数であることが要求される.解決方法としては, \(\psi\) の冪級数展開を用いるのが素直な方法である.すなわち \(x\) の連続するベキ係数は, 波動関数の \(\psi\) にそのベキ級数を代入することで決定される.しかし, この \(x\) の値が正または負の大きな領域における \(\psi\) の形を決定する問題やその後に続く \(x\) が小さいときの \(\psi\) の挙動問題で利用できる非常に有用な手法がある.それは, 因子を冪級数の形(後でそれは多項式に還元される)で導入して議論するやり方である.この手法は「多項式法」(polynomial method)と呼ぶことが出来るであろう [1] A.Sommerfeld, “Wave Mechanics”, p.11 .
最初の手順は \(|x|\) が非常に大きいときの波動方程式の漸近解を求めることである.エネルギー定数 \(W\) がどんな値であっても, それ以上に大きな \(|x|\) では \(a^{2}x^{2}\) に対し \(\lambda\) が無視できる程小さいと見做せるような \(|x|\) 値を見つけられる場合, 波動方程式の漸近形は次のようになる:
\frac{d^{2}\psi}{dx^{2}}=\alpha^{2}x^{2}\psi
\tag{11-3}
\end{equation}
漸近的な場合, この方程式を満足するのは, 次の様な指数関数である:
\psi = e^{\pm \frac{\alpha}{2}x^{2}}
\end{equation*}
なぜなら, このときの \(\psi\) の導関数は,
\begin{align*}
\frac{d\psi}{dx}&=\pm \alpha x\,e^{\pm\frac{\alpha}{2}x^{2}},\\
\frac{d^{2}\psi}{dx^{2}}&=\alpha^{2}x^{2}\,e^{\pm\frac{\alpha}{2}x^{2}}\pm
\alpha\,e^{\pm\frac{\alpha}{2}x^{2}}
\end{align*}
となり, そして \(\displaystyle{\frac{d^{2}\psi}{dx^{2}}}\) の第2項目は考えている領域では無視できるからである.
二つの漸近解 \(\displaystyle{e^{-\frac{\alpha}{2}x^{2}}}\) と \(\displaystyle{e^{+\frac{\alpha}{2}x^{2}}}\) のうち, 後者の解は \(|x|\) が増大するに従って急激に無限大になって行く傾向を持つので, 波動関数としては不適である.しかし, 前者の解は問題を適切に処理するものとなる.
その次に行うのは, 因子として \(x\) の冪級数を導入して波動関数の中に代入してその係数を決定することで, 配位空間 \((-\infty<x<\infty)\) に渡って波動関数の厳密解を得ることである.
\(\displaystyle{\psi=e^{-\frac{\alpha}{2}x^{2}}f(x)}\) としよう.すると式 (11-2) より
\begin{align*}
\frac{d^{2}\psi}{dx^{2}}&=e^{-\frac{\alpha}{2}x^{2}}\big\{ \alpha^{2}x^{2}f-\alpha f
-2\alpha xf +f”\big\}\\
&=(\alpha^{2}x^{2}-\lambda)\psi(x)=(\alpha^{2}x^{2}-\lambda)e^{-\frac{\alpha}{2}x^{2}}f(x)\\
&=e^{-\frac{\alpha}{2}x^{2}}\{\alpha^{2}x^{2}f-\lambda f\}
\end{align*}
ただし \(f’\) と \(f”\) はそれぞれ \(\displaystyle{\frac{df}{dx}}\) と \(\displaystyle{\frac{d^{2}f}{dx^{2}}}\) を表している.従って, 式 (11-2) は \(\displaystyle{e^{-\frac{\alpha}{2}x^{2}}}\) で除算することで次となる:
f” -2\alpha x f’ +(\lambda-\alpha)f = 0
\tag{11-4}
\end{equation}
このとき \(\alpha^{2}x^{2}f\) を含んだ項は打ち消し合ってしまう.
ここで, 便宜的に新しい変数 \(\xi\) を導入する.それは \(x\) と次の関係式で結び付いている:
\xi = \sqrt{\alpha}\,x,\quad \rightarrow\
\frac{df}{dx}=\sqrt{\alpha}\frac{dH}{d\xi},
\quad \frac{d^{2}f}{dx^{2}}=\alpha\frac{d^{2}H}{d\xi^{2}}
\tag{11-5}
\end{equation}
そして関数 \(f(x)\) を等価な \(H(\xi)\) で置き換え (その後, 全体を \(\alpha\) で除算する).すると微分方程式 (11-4) は次となる:
\frac{d^{2}H}{d\xi^{2}}-2\xi \frac{dH}{d\xi} + \left(\frac{\lambda}{\alpha}-1\right) H = 0
\tag{11-6}
\end{equation}
今度は \(H(\xi)\) を冪級数で表現し, その導関数を得るために微分する:
\begin{align*}
H(\xi)&=\sum_{\nu}a_{\nu}\xi^{\nu}=a_0+a_1\xi + a_2\xi^{2}+\dotsb,\\
\frac{dH}{d\xi}&=\sum_{\nu}\nu a_{\nu}\xi^{\nu-1}
=a_1+2a_{2}\xi + 3a_{3}\xi^{2}+\dotsb,\\
\frac{d^{2}H}{d\xi^{2}}&=\sum_{\nu}\nu(\nu-1)a_{\nu}\xi^{\nu-2}
=1\cdot2a_{2}+2\cdot3a_3\xi+\dotsb,
\end{align*}
これらの式を代入すると, 式 (11-6) は次のような形になるはずである:
\begin{align*}
&1\cdot2a_2+2\cdot3a_3\xi+3\cdot4a_4\xi^{2}+4\cdot5a_5\xi^{3}+\dotsb\\
&\quad-2a_1\xi-2\cdot2a_2\xi^{2}-2\cdot3a_3\xi^{3}-\dotsb\\
&\quad+\left(\frac{\lambda}{\alpha}-1\right)a_0+\left(\frac{\lambda}{\alpha}-1\right)a_1\xi +
\left(\frac{\lambda}{\alpha}-1\right)a_2\xi^{2}+\left(\frac{\lambda}{\alpha}-1\right)a_3\xi^{3}
+\dotsb = 0
\end{align*}
この冪級数が全ての \(\xi\) の値に対してゼロとなるためには (すなわち,\(H(\xi)\) が式 (11-6) の解となるためには), 各々の \(\xi\) のベキの係数が個々にゼロでなければならない:
\begin{align*}
\xi^{0}:\quad &1\cdot2a_2+\left(\frac{\lambda}{\alpha}-1\right)a_0=0\\
\xi^{1}:\quad &2\cdot3a_3+\left(\frac{\lambda}{\alpha}-1-2\right)a_1=0\\
\xi^{2}:\quad &3\cdot4a_4+\left(\frac{\lambda}{\alpha}-1-2\cdot2\right)a_2=0\\
\xi^{3}:\quad &4\cdot5a_5+\left(\frac{\lambda}{\alpha}-1-2\cdot3\right)a_3=0\\
&\quad \dotsb \dotsb
\end{align*}
または, 一般的に \(\xi^{\nu}\) の係数は次となる:
(\nu+1)(\nu+2)a_{\nu+2}+\left(\frac{\lambda}{\alpha}-1-2\nu\right)a_{\nu}=0
\end{equation*}
すなわち
a_{\nu+2}=-\frac{\left(\frac{\lambda}{\alpha}-2\nu-1\right)}{(\nu+1)(\nu+2)}a_{\nu}
\tag{11-7}
\end{equation}
この表現式は「再帰的公式(漸化式)」(recursive formula) と呼ばれている.これにより係数 \(a_2\),\(a_3\),\(a_4\),\(\dotsb\) が, 任意の値である \(a_0\) と \(a_1\) の表現で次々に計算する(表わす)ことが出来る.もし \(a_0\) をゼロとするならば, 奇数ベキの項だけが出現する;\(a_1\) をゼロとする場合には級数は偶数ベキの項だけを含むことになる.
エネルギーパラメータ \(\lambda\) が任意の値を取る場合, 上記の級数は無限個の項から成るので, 波動関数を満たすものには相当しない.なぜなら, その級数の値は \(x\) が増すに連れて急激に大きくなり, その結果, 全体の関数は, 例えそれが負の指数因子を含んでいたとしても \(x\) が増すに連れて無限に増大してしまうからである.このことを証明するために \(H\) の級数と \(e^{\xi^{2}}\) の級数,
\begin{align*}
&e^{\xi^{2}}=1+\xi^{2}+\frac{\xi^{4}}{2!}+\frac{\xi^{6}}{3!}+\dotsb
+\frac{\xi^{\nu}}{(\nu/2)!}+\frac{\xi^{\nu+2}}{(\nu/2+1)!}+\dotsb, \\
\quad &\rightarrow\quad b_{\nu}=\frac{1}{(\nu/2)!},\quad b_{\nu+2}=\frac{1}{(\nu/2+1)!},\\
\quad &\rightarrow\ b_{\nu+2}=\frac{1}{(\nu/2+1)!}=\frac{1}{(\nu/2+1)\cdot(\nu/2)!}
=\frac{1}{(\nu/2+1)}b_{\nu}=\frac{2}{\nu+2}b_{\nu}\sim \frac{2}{\nu}b_{\nu}
\tag{1}
\end{align*}
とを比較してみよう.\(\xi\) の値が大きい場合, これらの級数の最初の方の項たちは重要ではないであろう.そこで \(H(\xi)\) と \(e^{\xi^{2}}\) の級数展開の \(\nu\) 番目の項の係数の比を \(c\) と呼ぶことにしよう.すなわち \(e^{\xi^{2}}\) の級数展開の項 \(\xi^{\nu}\) の係数を \(b_\nu\) とすれば \(a_{\nu}/b_{\nu}=c\)であるが, これは大きいかも知れないし小さいかも知れない.\(\nu\) 値が十分に大きい場合, 式 (11-7) で \(\lambda\) を無視すれば (また \(\nu+1\simeq \nu\)など, とすれば),
a_{\nu+2}\approx -\frac{\left(-2\nu-1\right)}{(\nu+1)(\nu+2)}a_{\nu}
=\frac{2\nu+1}{(\nu+1)(\nu+2)}a_{\nu}\sim \frac{2\nu}{\nu\cdot\nu}a_{\nu}
=\frac{2}{\nu}a_{\nu}
\tag{2}
\end{equation*}
よって, 式 (1) と式 (2) より次の様な漸近的関係が得られる:
a_{\nu+2}=\frac{2}{\nu}a_{\nu},\qquad b_{\nu+2}=\frac{2}{\nu}b_{\nu}
\end{equation*}
従って \(\nu\) が十分に大きい場合には, 次とすることが出来る:
\frac{a_{\nu+2}}{b_{\nu+2}}=\frac{a_\nu}{b_\nu}=c
\end{equation*}
よって, \(H\) の高次の級数項たちは \(e^{\xi^{2}}\) のそれとは, 定数が掛け合わされているだけの違いに過ぎない.従って \(|\xi|\) が大きな値である場合には低次の項は重要でないので, \(H\) は \(e^{\xi^{2}}\) の様に振る舞うであろう.そして積 \(e^{-\xi^{2}/2}H\) は, その領域で \(e^{+\xi^{2}/2}\) の様に振る舞うであろう.よって, それを波動関数として受け入れることは出来ない.
従って, エネルギーパラメータの値は \(H\) の級数が有限な項数で打ち切られて多項式となるように選ばなければならない.それは波動関数を満たすものとなる.なぜなら, 負の指数関数因子 \(e^{-\xi^{2}/2}\) は \(|\xi|\) が大きな値のとき関数をゼロに近づけるからである.\(n\) 番目の項で級数を打ち切らす \(\lambda\) の値は式 (11-7) から (分子がゼロとなるとして), 次であることが分かる:
\frac{\lambda}{\alpha}-2n-1=0,\quad\rightarrow\quad \lambda = (2n+1)\alpha
\tag{11-8}
\end{equation}
さらには, \(n\) が偶数か奇数かに従って, \(a_0\) と \(a_1\) の何方かの値をゼロにすることも必要である.と言うのは, \(\lambda\) を適切に選択すると, 偶数系列と奇数系列の何方かが途切れることはあっても, 両方が途切れることはないからである.従って, 解は \(\xi\) の偶関数か奇関数の何れかである.この条件は, 波動方程式 (11-2) が満足の行く解を持つことを保証するための十分条件であり, そしてさらには必要条件でもある.つまり他の \(\lambda\) では満足の行く解とはならないのである.振動子状態の量子数と呼んで良いであろう整数 \(n\) の各値 \(0,1,2,3,\dotsb\) に対して波動方程式の満足解が存在する.波動方程式の取り扱いに量子数が多項式 \(H(\xi\) の次数として入るのは, 古い量子論で位相積分に \(h\) の整数倍や半整数倍を任意に仮定していたことと比較すると, 特に納得のいくものである.
\(n\) 番目の波動関数の存在を式 (11-8) で表現するならば, \(\lambda\) と \(\alpha\) をそれが表わす量 \(\lambda = 8\pi^{2}mW/h^{2}\), \(\alpha=4\pi^{2}m\nu_0/h\) で置き換えるとき次となる:
\frac{8\pi^{2}mW}{h^{2}}&=(2n+1)\frac{4\pi^{2}m\nu_0}{h},\notag \\
\quad \to \quad
W &= W_n = \left(n+\frac{1}{2}\right)h\nu_0, \quad n = 0,1,2,\dotsb
\tag{11-9}
\end{align}
第 6a 節での古い量子論によって得られた結果式 \(W=nh\nu_0\) と比較すると, すべてのエネルギー準位が, 図 11-1 に示されているように準位間の半分の量, いわゆる零点エネルギー \(h\nu_0/2\) だけ上にシフトする違いがあるだけである.それから分かることは, 系がたとえ最低準位にあっても, 平衡点に静止しているときに持つであろう量よりも大きいエネルギーを持っていることである.実験との一致を高めるゼロ点エネルギーの存在は, 量子力学の重要な特徴であり,多くの問題で繰り返される [2]絶対零度に近い温度で環境と熱力学的に平衡状態にある系は, この定常状態にあることになるので, 零点エネルギーは, … Continue reading.古い量子論の扱いと全く同様に, 隣り合うエネルギー準位間での遷移によって放出または吸収される周波数は古典的な振動周波数 \(\nu_0\) に等しい.
11b. 調和振動子の波動関数とその物理的解釈
エネルギーの特性値 \(W_n\) の各々について, 再帰式 (11-7) を用いて波動方程式 (11-1) の満足な解を構築することが出来る.このように, 各々独立した波動関数が 1 つだけ対応するエネルギー準位は, 複数の独立した波動関数が対応する「縮退」(degenerate)したエネルギー準位 (その例は後で考察する) と区別して,「非縮退」(non-degenerate)と呼ばれる.式 (11-1) の解は次の形に書くことが出来る:
\psi_n(x)=N_n\,e^{-\xi^{2}/2}H_n(\xi),\quad\text{where}\quad \xi=\sqrt{\alpha}\,x
\tag{11-10}
\end{equation}
\(H_n(\xi)\) は \(\xi\) について \(n\) 次の多項式であり, そして \(N_n\) は \(\psi_n\) が規格化されるように調整された定数である.すなわち \(\psi_n\) が次の関係式を満たすように決められるのである:
\int_{-\infty}^{\infty}\psi_n^{*}(x)\psi_n(x)\,dx = 1
\tag{11-11}
\end{equation}
ただし \(\psi_n\) の複素共役である \(\psi_n^{*}\) はこの場合 \(\psi_n\) に等しい.次の節ではこれらの解 \(\psi_n\) の性質や特性を詳しく議論する.その最初の, すなわち系の最低エネルギー状態に相当する関数は次である:
\psi_0(x)=\left(\frac{\alpha}{\pi}\right)^{1/4}\,e^{-\frac{\xi^{2}}{2}}
=\left(\frac{\alpha}{\pi}\right)^{1/4}\,e^{-\frac{\alpha}{2}x^{2}}
\tag{11-12}
\end{equation}
これらの関数を図 11-2 に示す.第 10a 節で議論した公理から \(\psi_0^{*}\psi_0=\psi_0^{2}\) であり, これは座標 \(x\) に対する確率分布関数を表わすもので, 図にはこれもプロットされている.言い換えると, 任意の点 \(x\) での量 \(\psi_0^{2}(x)dx\) は, その点の範囲 \(dx\) に粒子を見出す確率を与える.この場合の量子力学の結果は, 同じエネルギーを持つ調和振動子について古典的に計算した確率関数と全く同じであるとは言えないことが, 図から分かる.古典的に粒子は, 明確に定義される運動の端点で見出されやすい (古典的な確率分布は図中の点線で示されている).それに対し \(\psi^{2}_0\) は \(x\) の原点に極大点を持っており, 更には, 古典的に許される領域の外でも粒子を発見する確率は急激に減少して行くがしかし有限であることを示している.
この驚くべき結果は, 全エネルギーがポテンシャルエネルギーよりも小さい領域にも粒子が侵入出来ることを意味するが, これは「粒子の位置と速度を同時に正確に測定することは不可能である」ことを結論するハイゼンベルグの不確定性原理と密接に関係している.この現象については第12章で更に議論するであろう.しかしながら,「運動エネルギーが負となる領域に確率分布関数が拡がっても, エネルギー保存則を破棄する必要はない」ということはこの時点でも言える.
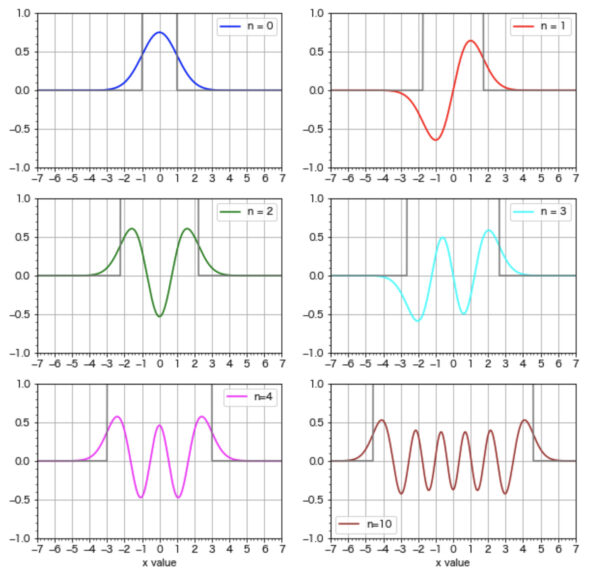
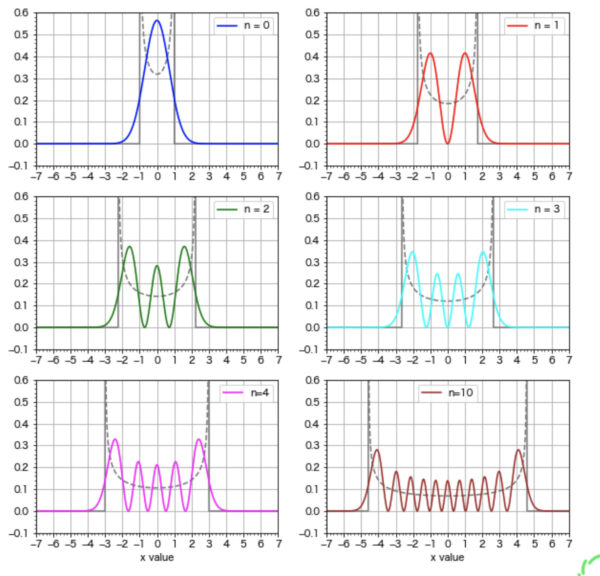
\(n\) の値が大きい場合の \(\psi_n\) の形が図 11-3 に示されている.\(H_n\) は次数 \(n\) の多項式なので, \(\psi_n\) は \(n\) 個の零点 (zeros), すなわち \(\psi_n\) がゼロの線を横切る点を持つことになる.それらの点で粒子を見出す確率はゼロである.図 11-3 を調べると, プロットされている全ての解の振舞いは, 第 9c 節の一般的な議論で得られた事柄に一致することを示している;すなわち, 粒子の運動が古典的に許される (\(V(x)\) が \(W_n\)よりも小さい) 領域内で, 波動関数は \(n\) 個の零点を持って振動し, 他方その領域外での波動関数は指数関数的に急激にゼロへと減少して行き零点を持たたい.さらに, この例では更に別の一般原理も図示していることが分かる;すなわち, 値 \(n\) が大きくなるほど, 波動力学的な確率分布関数は同じエネルギーの粒子に対する古典的な表現式に益々近くなって行くことである.次の図 11-4 で示しているのは, 図11-3 の各状態関数の絶対値の2乗 \(|\psi(x)|^{2}\) とエネルギーが同じ値の古典的な調和振動子の確率曲線との比較である [3]図中の破線は古典的な振動子の確率密度 \(\rho(x)\) を示している.この \(\rho(x)\) の描画は, Bernd Thaller : 「Visual Quantum Mechanics」の第 7.2 … Continue reading .
波動力学曲線の急激な変動を除けば, 2つの関数の一般的な一致は良好である.この一致により我々は, 波動力学的調和振動子における粒子の運動は, 古典的な往復運動と同様に, 粒子はその軌道の中心で速度を上げ, 平衡位置からの最大変位に近づくと速度を下げると思い描くことが出来る.振動の振幅は, 古典的振動子の場合のように一定であると考えることは出来ない;その代わりに, 粒子は時には大きな振幅で, そして時には非常に小さな振幅で振動しているが, 通常は同じエネルギーでの古典的値に近い振幅で振動していると思い描くことが出来る.振動子の他の特性もこの描像に適合する;従って波動力学的な運動量の二乗平均平方根は古典的な値と等しくなる.
このタイプの描像は, 波動力学的な式を直感的に把握するには有益であるけれども, あまり厳密的に受け止めてはならない.なぜなら, それは完全に申し分のない描像であるとは言えないからである.従って,「波動関数に存在する零点は, 確率分布関数が殆どゼロに近くなる点に相当する定常状態に一致する」とすることは出来ない.
11.c 調和振動子の波動関数の数学的特性
調和振動子の波動方程式解で得られる多項式 \(H_n(\xi)\) と関数 \(e^{-\frac{\xi^{2}}2}H_n(\xi)\) はシュレディンガーの研究から始まったわけではないが, 他の問題との関係で数学者にはよく知られるようになった.それらの特性は詳しく研究されてきた.
式 (11-7) で与えられている係数間の関係が目下の目標なので,「エルミート多項式」(Hermite polynomials)と呼ばれる多項式 \(H_n(\xi)\) の理論を展開する代わりに, 別の定義によってそれらを導入するのが便利である:
H_n(\xi)=(-1)^{n}e^{\xi^{2}}\frac{d^{n}e^{-\xi^{2}}}{d\xi^{n}}
\tag{11-13}
\end{equation}
これが式 (11-7) と同じ関数となることは後で示すであろう.第3の定義は「母関数」(generating function) の使用と関係がある.その方法は多くの計算で有益であり, また他の関数に適用することも出来る.エルミート多項式の母関数は次である:
\[S(\xi,s)\equiv e^{\xi^{2}-(s-\xi)^{2}}\equiv \sum_{n=0}^{\infty}\frac{H_n(\xi)}{n!}s^{n}\tag{11-14}\]
補助変数 \(s\) のあるこの恒等式が意味するのは,「関数 \(e^{\xi^{2}-(s-\xi)^{2}}\) は \(s\) のベキ級数に展開すると \(s\) の連続するベキ係数がちょうどエルミート多項式 \(H_n(\xi)\) に \(1/n!\) をかけ合わせたものになる」と言うことである.式 (11-13) と式 (11-14) の2つの定義が等価であることを示すために, \(S\) を \(s\) に関して \(n\) 回微分し \(s\) を \(0\) に近づけると, \(S\) に関する式を 1 つずつ使って, \(\nu<n\) の項は微分によって消え, \(\nu>n\) の項は \(s\to0\) に対して消え, \(\nu=n\) の項だけが残る:
\begin{align*}
\left(\frac{\partial^{\ n}S}{\partial s^{n}}\right)_{s\to0}
&=\left(\frac{\partial^{\ n}}{\partial s^{n}}\sum_{\nu}\frac{H_{\nu}(\xi)s^{\nu}}{\nu!}
\right)_{s\to 0} = H_n(\xi),\\
\left(\frac{\partial^{\ n}S}{\partial s^{n}}\right)_{s\to0}&=
\left(\frac{\partial^{\ n}e^{\xi^{2}-(s-\xi)^{2}}}{\partial s^{n}}\right)_{s\to0}
=e^{\xi^{2}}\left(\frac{\partial^{\ n}e^{-(s-\xi)^{2}}}{\partial(s-\xi)^{n}}\right)_{s\to0}
=e^{\xi^{2}}(-1)^{n}\left(\frac{\partial^{\ n}e^{-(s-\xi)^{2}}}{\partial \xi^{n}}\right)_{s\to0}\\
&=(-1)^{n}e^{\xi^{2}}\frac{d^{n}e^{-\xi^{2}}}{d\xi^{n}}
\end{align*}
これら2つの式を比較すると式 (11-13) が得られるので, 2つの \(H_n(\xi)\) の定義は等価であることが分かる.式 (11-13) は個々の関数形を求めるのに便利であり, 他方式 (11-14) はそれらの特性, 例えば今から議論するような特性, を導出するとき便利であることが多い.
上で定義した関数が調和振動子問題の解に用いられる関数と同じであることを示すために, \(H_n(\xi)\) が満たす微分方程式を探してみる.導出するのに最も好都合なのは, 連続するエルミート多項式及びその導関数の確実な関係式を導出することである.\(S=e^{\xi^{2}-(s-\xi)^{2}}\) なのでその \(s\) についての偏微分は次式で与えられる:
\def\ppdiff#1#2{\frac{\partial #1}{\partial #2}}
\ppdiff{S}{s}=-2(s-\xi)S
\end{equation*}
同様に, 級数 \(S=\sum \frac{H_n(\xi)}{n!}s^{n}\) を偏微分し, \(\partial S/\partial s\) の2つの異なる表現式を等しいとするならば, 次式が得られる:
\sum_{n}\frac{H_n(\xi)}{(n-1)!}s^{n-1}=-2(s-\xi)\sum_n \frac{H_n(\xi)}{n!}s^{n}
\end{equation*}
または, \(s\) の同じベキに相当する項を集めるならば,
\sum_n \left\{\frac{H_{n+1}(\xi)}{n!}+2\frac{H_{n-1}(\xi)}{(n-1)!}-2\xi\frac{H_n(\xi)}{n!}
\right\}s^{n}=0
\end{equation*}
この式は \(s\) の全値について真であるので, \(s\) の個々のベキの係数はゼロとなるべきである.よって \(\{\ \}\) 内はゼロであり, それに \(n!\) をかけ合わせることで, エルミート多項式の再帰的公式が与えられる:
H_{n+1}(\xi)-2\xi H_n(\xi)+2nH_{n-1}(\xi)=0
\tag{11-15}
\end{equation}
同様に, \(\xi\) で偏微分すると次式が導出される:
\ppdiff{S}{\xi}=2sS
\end{equation*}
これは, 上と全く同様にして次式を与える:
\sum_n\left\{\frac{H’_n(\xi)}{n!}s^{n}-2\frac{H_n(\xi)}{n!}s^{n+1}\right\}=0
\end{equation*}
または,
H’_n(\xi)=\frac{dH_n(\xi)}{d\xi}=2nH_{n-1}(\xi)
\tag{11-16}
\end{equation}
これにはエルミート多項式の1次導関数が含まれている.これを更に \(\xi\) で微分すれば, より高次の導関数を含んだ式が得られる.
式 (11-15) と式 (11-16) からは \(H_n(\xi)\) に対する微分方程式が導出される.式 (11-16) から得られるのは,
H”_{n}(\xi)=2nH’_{n-1}(\xi)=4n(n-1)H_{n-2}(\xi),
\tag{11-17}
\end{equation}
他方, 式 (11-15) は次のように書き換えることが出来る:
H_n(\xi)-2\xi H_{n-1}(\xi)+2(n-1)H_{n-2}(\xi)=0
\tag{11-18}
\end{equation}
式 (11-16) と式 (11-17) を用いると, これは次となる:
&H_n(\xi)-\frac{2\xi}{2n}H’_n(\xi)+\frac{1}{2n}H”_n(\xi)=0,\notag \\
&\text{or}\quad H”_n(\xi) -2\xi H’_n(\xi)+2n H_n(\xi)=0
\tag{11-19}
\end{align}
これは, 式 (11-8) で要求されているように \(\displaystyle{\frac{\lambda}{\alpha}-1}\) の所を \(2n\) に置き換えるならば, まさに調和振動子問題で得られた式 (11-6) となる.全ての整数値 \(n\) に対して, この方程式は無限大で正しい振舞いをする解を一つだけ持つので, 第 11a 節で導入した多項式 \(H_n(\xi)\) はエルミート多項式である.
次の関数は「エルミート直交関数」(Hermite orthogonal functions)と呼ばれる:
\psi_n(x)=N_n\,e^{-\frac{\xi^{2}}{2}}H_n(\xi),\quad \xi = \sqrt{\alpha}\,x
\tag{11-20}
\end{equation}
これらが調和振動子の波動関数であることは前に見たことである.値 \(N_n\) は \(\psi_n\) を規格化するもの, つまり \(\displaystyle{\int_{-\infty}^{\infty}\psi_n^{2}(x)\,dx=1}\) とする規格化定数で,
N_n = \left\{\left(\frac{\alpha}{\pi}\right)^{1/2}\frac{1}{2^{n}n!}\right\}^{1/2}
\tag{11-21}
\end{equation}
配位空間に於いて任意の2関数の積を積分したときにゼロとなる場合, それらは互いに直交している:
&\int_{-\infty}^{\infty}\psi_n(x)\psi_m(x)\,dx=0,\quad n\ne m
\tag{11-22}\\
\rightarrow&\quad N_{n}N_{m}\int_{-\infty}^{\infty}
e^{-\frac{\xi^{2}}{2}}H_n(\xi)\,e^{-\frac{\xi^{2}}{2}}H_m(\xi)\,\frac{d\xi}{\sqrt{\alpha}}
=\delta_{n,m}\notag
\end{align}
関数の直交性の証明と式 (11-21) の規格化定数を見積もるのには, 次の2つの「母関数」(generating function) を考えるのが便利である:
\begin{align*}
S(\xi,s)&=\sum_n \frac{H_n(\xi)}{n!}s^{n} = e^{\xi^{2}-(s-\xi)^{2}},\\
T(\xi,t)&=\sum_m \frac{H_m(\xi)}{m!}s^{n}=e^{\xi^{2}-(t-\xi)^{2}}
\end{align*}
これらを用いると, 次のような関係式が得られる:
\begin{align*}
\int_{-\infty}^{\infty}ST\,e^{-\xi^{2}}\,d\xi
&=\sum_n\sum_m\frac{s^{n}t^{m}}{n!m!}\int_{-\infty}^{\infty}H_n(\xi)H_m(\xi)\,e^{-\xi^{2}}\,d\xi\\
&=\int_{-\infty}^{\infty}e^{-s^{2}-t^{2}+2s\xi+2t\xi-\xi^{2}}\,d\xi\\
&=e^{2st}\int_{-\infty}^{\infty}e^{-(\xi-s-t)^{2}}\,d(\xi-s-t)
=\sqrt{\pi}\,e^{2st}\\
&=\sqrt{\pi}\sum_n\frac{(2st)^{n}}{n!}
=\sum_n s^{n}t^{n}\sqrt{\pi}\frac{2^{n}}{n!}\\
\rightarrow\quad
\sum_m s^{n}t^{m}\frac{1}{n!m!}&\int_{-\infty}^{\infty}H_n(\xi)H_m(\xi)\,e^{-\xi^{2}}\,d\xi
=s^{n}t^{n}\sqrt{\pi}\frac{2^{n}}{n!}\\
\int_{-\infty}^{\infty}H_n(\xi)&\,e^{-\frac{\xi^{2}}{2}}H_m(\xi)\,e^{-\frac{\xi^{2}}{2}}\,d\xi
=\frac{\sqrt{\alpha}}{N_nN_m}\delta_{n\,m}\ \rightarrow\
s^{n}t^{n}\frac{\sqrt{\alpha}}{N_n^{2}n!n!}=s^{n}t^{n}\sqrt{\pi}\frac{2^{n}}{n!}\\
\rightarrow\quad
\frac{\sqrt{\alpha}}{N_n^{2}}&=2^{n}n!\sqrt{\pi},\ \rightarrow\
N_n^{2}=\frac{\sqrt{\alpha}}{\sqrt{\pi}\,2^{n}n!}
\end{align*}
2つの等しい級数展開に於ける \(s^{n}t^{m}\) の係数を比較することで, 積分 \(\int_{-\infty}^{\infty}H_n(\xi)H_m(\xi)\,e^{-\xi^{2}}\,d\xi\)は\(m\ne m\) の場合にゼロとなり, \(m=n\) のときには \(2^{n}n!\sqrt{\pi}\) となることが分かる.その結果, 関数は直交性を有し規格化定数が上記の値となると言える.
エルミート多項式の最初の方を幾つか示しておく:
H_0(\xi)&= 1\notag \\
H_1(\xi)&= 2\xi\notag\\
H_2(\xi)&= 4\xi^{2}-2\notag\\
H_3(\xi)&= 8\xi^{3}-12\xi\notag\\
H_4(\xi)&= 16\xi^{4}-48\xi^{2}+12\notag\\
H_5(\xi)&= 32\xi^{5}-160\xi^{3}+120\xi\tag{11-23}\\
H_6(\xi)&= 64\xi^{6}-480\xi^{4}+720\xi^{2}-120\notag\\
H_7(\xi)&= 128\xi^{7}-1344\xi^{5}+3360\xi^{3}-1680\xi\notag\\
H_8(\xi)&= 256\xi^{8}-3584\xi^{6}+13440\xi^{4}-13440\xi^{2}+1680\notag\\
H_9(\xi)&= 512\xi^{9}-9216\xi^{7}+48384\xi^{5}-80640\xi^{3}+30240\xi\notag\\
H_10(\xi)&= 1024\xi^{10}-23040\xi^{8}+161280\xi^{6}-403200\xi^{4}+302400\xi^{2}-30240\notag
\end{align}
このリストは, 式 (11-15) の漸化式を用いることで容易に拡張することが出来る.波動関数, すなわち式 (11-20) で与えられる関数の曲線の最初の幾つかを図11-3 に示しておく.
母関数 \(S\) と \(T\) を利用すると, \(\psi_n\) を含む重要な積分の幾つかを見積もることが出来る.例えば, 状態 \(n\) から状態 \(m\) への遷移する確率を決定する積分を研究すること(後の第 40c 節で示す) が出来る.それは次である:
x_{nm}=\int_{-\infty}^{\infty} \psi_n x \psi_m\,dx
=\frac{N_nN_m}{\alpha}\int_{-\infty}^{\infty} \xi H_n H_m\,e^{-\xi^{2}}\,d\xi
\tag{11-24}
\end{equation}
\(S\) と \(T\) を用いると次の関係式を得る:
\begin{align*}
\int_{-\infty}^{\infty} ST\,e^{-\xi^{2}}\xi\,d\xi
&=\sum_n\sum_m \frac{1}{n!m!}s^{n}t^{m}\int_{-\infty}^{\infty}H_nH_m\,e^{-\xi^{2}}\xi\,d\xi\\
&=e^{2st}\int_{-\infty}^{\infty}e^{-(\xi-s-t)^{2}}\xi\,d\xi\\
&=e^{2st}\int_{-\infty}^{\infty}e^{-(\xi-s-t)^{2}}(\xi-s-t)\,d(\xi-s-t)\\
&\qquad +e^{2st}(s+t)\int_{-\infty}^{\infty}e^{-(\xi-s-t)^{2}}\,d(\xi-s-t)
\end{align*}
最初の積分は(被積分因子が奇関数なので) ゼロとなり, そして2番めの積分は公式:
\(\displaystyle{\int_{-\infty}^{\infty} e^{-ax^{2}}dx=\sqrt{\frac{\pi}{a}}}\) より \(\sqrt{\pi}\) を与える.そして指数関数を展開すると次となる:
\begin{align*}
\sqrt{\pi}\bigg(s+2s^{2}t&+\frac{2^{2}s^{3}t^{2}}{2!}+\dotsb +\frac{2^{n}s^{n+1}t^{n}}{n!}
+\dotsb \\
\qquad &+t+2st^{2}+\frac{2^{2}s^{2}t^{3}}{2!}+\dotsb+\frac{2^{n}s^{n}t^{n+1}}{n!}
+\dotsb \bigg)
\end{align*}
従って \(s^{n}t^{m}\) の係数を比較するならば, \(x_{nm}\) の値は \(m=n\pm1\) のとき,
x_{n,n+1}&=\sqrt{\frac{n+1}{2\alpha}}, \tag{11-25a}\\
x_{n,n-1}&=\sqrt{\frac{n}{2\alpha}}\tag{11-25b}
\end{align}
となり, それ以外はゼロとなることが分かる.「この結果は, 調和振動子の隣り合うエネルギー準位間でのみ遷移が起こることを要求している」ことが後に示されるであろう.それは第 5c 節の「対応原理」(correspondence principle 量子力学は量子数の大きな極限で古典力学の結果と一致するという原理. から引き出される結論と一致することである [4]【 参考 】 式 (11-24) に式 (11-15) の再帰的公式を用いる方法で考えてみる.式(11-15)から, \[\xi H_n = \frac{1}{2}H_{n+1}+nH_{n-1}\] なので, これを式 (11-24) … Continue reading .
References
| ↑1 | A.Sommerfeld, “Wave Mechanics”, p.11 |
|---|---|
| ↑2 | 絶対零度に近い温度で環境と熱力学的に平衡状態にある系は, この定常状態にあることになるので, 零点エネルギーは, 最も低い定常状態にある系のエネルギーとして使われる.ゼロ点エネルギーは, 多くの統計力学や熱力学の議論において非常に重要である.ゼロ点エネルギーの存在は不確定性原理と関連がある. |
| ↑3 | 図中の破線は古典的な振動子の確率密度 \(\rho(x)\) を示している.この \(\rho(x)\) の描画は, Bernd Thaller : 「Visual Quantum Mechanics」の第 7.2 節の記述に基づいている.その部分の訳文を以下に示しておくこととする.—————
|
| ↑4 | 【 参考 】 式 (11-24) に式 (11-15) の再帰的公式を用いる方法で考えてみる.式(11-15)から, \[\xi H_n = \frac{1}{2}H_{n+1}+nH_{n-1}\] なので, これを式 (11-24) に代入すると, \begin{align*} x_{nm}&=\frac{N_nN_m}{\alpha}\int_{-\infty}^{\infty}\xi\,H_n H_m\,e^{-\xi^{2}}\,d\xi \\ &=\frac{N_nN_m}{\alpha}\int_{-\infty}^{\infty} \left(\frac{1}{2}H_{n+1}+nH_{n-1}\right)H_m\,e^{-\xi^{2}}\,d\xi \\ &=\frac{N_nN_m}{2\alpha}\int_{-\infty}^{\infty} H_{n+1} H_m\,e^{-\xi^{2}}\,d\xi +\frac{nN_nN_m}{\alpha}\int_{-\infty}^{\infty}H_{n-1} H_m\,e^{-\xi^{2}}\,d\xi \tag{a} \end{align*} ここで規格直交性の式 (11-22) から, \begin{align*} &\int_{-\infty}^{\infty}H_{n-1}(\xi)H_m(\xi)\,e^{-\xi^{2}}\,d\xi = \frac{\sqrt{\alpha}}{N_{n-1} N_m}\delta_{n-1,m}\\ &\int_{-\infty}^{\infty}H_{n+1}(\xi)H_m(\xi)\,e^{-\xi^{2}}\,d\xi = \frac{\sqrt{\alpha}}{N_{n+1} N_m}\delta_{n+1,m} \tag{b} \end{align*} が言えるので, これらを式 (a) に用いると, \begin{align*} x_{nm}&= \frac{N_nN_m}{2\alpha}\frac{\sqrt{\alpha}}{N_{n+1} N_m}\delta_{n+1,m} +\frac{nN_nN_m}{\alpha}\frac{\sqrt{\alpha}}{N_{n-1} N_m}\delta_{n-1,m}\\ &=\frac{1}{2\alpha}\cdot\frac{N_n}{N_{n+1}}\delta_{m,n+1} +\frac{n}{\sqrt{\alpha}}\cdot\frac{N_n}{N_{n-1}}\delta_{m,n-1} \tag{c} \end{align*} 更に規格化定数の結果式 (11-21) を利用すると, \begin{align*} N_{n}&=\left\{\left(\frac{\alpha}{\pi}\right)^{1/2}\frac{1}{2^{n}n!}\right\}^{1/2},\\ \rightarrow\ N_{n+1}&=\left\{\left(\frac{\alpha}{\pi}\right)^{1/2}\frac{1}{2^{n+1}(n+1)!}\right\}^{1/2},\ N_{n-1}=\left\{\left(\frac{\alpha}{\pi}\right)^{1/2}\frac{1}{2^{n-1}(n-1)!}\right\}^{1/2} \end{align*} これより次が言える: \begin{equation*} \frac{N_n}{N_{n+1}}=\sqrt{2(n+1)},\qquad \frac{N_n}{N_{n-1}}=\frac{1}{\sqrt{2n}} \tag{d} \end{equation*} この式 (d) を式 (c) に代入するならば, 次式が得られる: \begin{align*} x_{nm}&=\frac{1}{2\alpha}\cdot\sqrt{2(n+1)}\delta_{m,n+1} +\frac{n}{\sqrt{\alpha}}\cdot\frac{1}{\sqrt{2n}}\delta_{m,n-1}\\ &=\sqrt{\frac{n+1}{2\alpha}}\delta_{m,n+1} + \sqrt{\frac{n}{2\alpha}}\delta_{m,n-1} \tag{e} \end{align*} 従って, 言い換えれば式 (11-25) となる: \begin{equation*} x_{n,n+1}=\sqrt{\frac{n+1}{2\alpha}},\qquad x_{n,n-1}=\sqrt{\frac{n}{2\alpha}} \tag{f} \end{equation*} |