ランダウ=リシッツ：「量子力学」の§103に次のような文章があった：
最終値 \(\Phi(+\infty)\) と始めの値 \(\Phi(-\infty)\) を結び付ける「散乱演算子」 \(\hat{S}\) の定義：\(\Phi(+\infty)=S\Phi(-\infty)\) から, もし衝突前に系が状態\(\Phi_i\)(ある自由粒子の集まり)にあれば, それが状態 \(\Phi_f\)(自由粒子の他の集まり)に遷移する確率振幅すなわち「遷移振幅」は行列要素 \(S_{fi}\) である．
これから,「\(S\)-行列」の行列要素 \(S_{mn}\) と「遷移振幅」 \(\lambda_{mn}\) は同じ量か? という疑問が湧いてしまった． そこで手元にある J.J.Sakurai と F.Mandl の文章を読んで, この疑問を考えてみることにした． 
まずは J.J.Sakurai著「Advanced Quantum Mechanics」の§ 4-2 を訳出したものを示す．
◎ このブログ記事をPDF化したものは次のリンクをクリックすることで見ることが出来る．またダウンロードボタンをクリックすることでダウンロードも可能である：
相互作用表示での\(S\)-行列展開
相互作用表示(Interaction representation)
この章では, 摂動論の有効性を前提に様々な物理過程を議論してみたい．第2章で用いた通常の時間依存摂動論は, 時空座標やエネルギー運動量変数が共変的に現れないため, 相対論的粒子を含む過程を扱うにはあまり便利ではない．そこで, ハミルトン形式の枠組みの中で,「相互作用表示」と呼ばれる表示を用いれば, 遷移行列を明らかに共変的に表現することが出来ることが分かった．この表示の有用性は, 1947年に朝永振一郎とJ.Schwingerによって初めて認識され, 量子場の理論に導入された． 通常のシュレーディンガー表示では, 状態ベクトル \(\Phi^{(S)}(t)\) の時間発展は, 次のシュレーディンガー方程式で与えられる：
\begin{equation} \def\pdiff#1{\frac{\partial}{\partial #1}} \def\reverse#1{\frac{1}{#1}} \def\Bppdiff#1#2{\frac{\partial^{2} #1}{\partial #2^{2}}} \def\ppdiff#1#2{\frac{\partial #1}{\partial #2}} \def\oodiff#1#2{\frac{d #1}{d #2}} \def\BK#1#2{\langle #1 | #2 \rangle} \def\BraKet#1#2#3{\langle #1 | #2 | #3 \rangle} \def\bra#1{\langle #1 |} \def\ket#1{| #1 \rangle} \def\mb#1{\mathbf{#1}} i\ppdiff{\Phi^{(S)}}{t}=H^{(S)}\Phi^{(S)} \tag{4.21} \end{equation}
ただし, 肩文字 \((S)\) はSchrödingerを表して(意味して)いる．\(H^{(S)}\) は２つの部分に分けることが出来る： \begin{equation} H^{(S)}=H_0^{(S)}+H_I^{(S)} \tag{4.22} \end{equation}
ただし \(H_0^{(S)}\) は摂動のない時のハミルトニアンであり, そして \(H_I^{(S)}\) は摂動を表している．場の理論に於いては, \(H_0^{(S)}\) は自由場のハミルトニアン, \(H_I^{(S)}\) は相互作用ハミルトニアン密度の空間積分とされる(後の式(4.41)を見よ)． ここで, 次の変換を考えよう： \begin{equation} \Phi(t)=e^{iH_0^{(S)}t}\Phi^{(S)},\qquad O(t)=e^{iH_0^{(S)}t}O^{(S)}e^{-iH_0^{(S)}t} \tag{4.23} \end{equation}
ただし \(O^{(S)}\) はシュレディンガー表示に於ける演算子である．この変換は,「シュレディンガー表示」から「相互作用表示」と呼ばれるものへ「表示を変更すること」と見做せる．上付き添字のない記号 \(\Phi(t)\) と \(O(t)\)は,「相互作用表示」に於ける「状態ベクトル」と「演算子」を表わし, 各々はシュレーディンガー表示に於ける \(\Phi^{(S)}\)と\(O^{(S)}\) に対応する．状態ベクトル \(\Phi(t)\) の時間発展は次式で与えられる： \begin{align} i\ppdiff{\Phi(t)}{t}&=i\pdiff{t}\left\{e^{iH_0^{(S)}t}\Phi^{(S)}\right\} =i\left[\ppdiff{\,e^{iH_0^{(S)}t}}{t}\Phi^{(S)}+e^{iH_0^{(S)}t} \ppdiff{\Phi^{(S)}}{t}\right]\notag\\ &=i\left[iH_0^{(S)}e^{iH_0^{(S)}t}\Phi^{(S)}+e^{iH_0^{(S)}t}\ppdiff{\Phi^{(S)}}{t}\right] =-H_0^{(S)}e^{iH_0^{(S)}t}\Phi^{(S)}+e^{iH_0^{(S)}t}\times i\ppdiff{\Phi^{(S)}}{t}\notag\\ &=-H_0^{(S)}e^{iH_0^{(S)}t}\Phi^{(S)}+e^{iH_0^{(S)}t}H^{(S)}\Phi^{(S)}\notag\\ &=-H_0^{(S)}e^{iH_0^{(S)}t}\Phi^{(S)}+e^{iH_0^{(S)}t}\bigl\{H_0^{(S)}+H_I^{(S)}\bigr\}e^{-iH_0^{(S)}t}e ^{iH_0^{(S)}t}\Phi^{(S)}\notag\\ &=-H_0^{(S)}e^{iH_0^{(S)}t}\Phi^{(S)}+e^{iH_0^{(S)}t}H_0^{(S)}\Phi^{(S)}+e^{iH_0^{(S)}t}H_I^{(S)} e^{-iH_0^{(S)}t}e^{iH_0^{(S)}t}\Phi^{(S)}\notag\\ &=e^{iH_0^{(S)}t}H_I^{(S)}e^{-iH_0^{(S)}t}\times e^{iH_0^{(S)}t}\Phi^{(S)},\notag\\ \therefore \quad i\ppdiff{\Phi}{t}&=H_I\Phi(t) \tag{4.24} \end{align}
ただし \(H_I\) は相互作用表示に於ける摂動ハミルトニアンである．一方, \(O^{(S)}\)と\(O\) は \(t=0\) では一致することに注意すると次を得る： \begin{equation} O(t)=e^{iH_0^{(S)}t}\,O(0)\,e^{-iH_0^{(S)}t} \tag{4.25} \end{equation}
この式からは, 次のような \(O\) に対する運動方程式が導かれる： \begin{align} \frac{d}{dt}O(t)&=\frac{d}{dt}\bigl\{e^{iH_0^{(S)}t}\,O(0)\,e^{-iH_0^{(S)}t}\bigr\}\notag\\ &=\bigl(iH_0^{(S)}\bigr)e^{iH_0^{(S)}t}\,O(0)\,e^{-iH_0^{(S)}t}+e^{iH_0^{(S)}t}\,O(0)\bigl(-iH_0^{(S)}\bigr) e^{-iH_0^{(S)}t}\notag\\ &=i\left\{H_0^{(S)}\left(e^{iH_0^{(S)}t}\,O(0)\,e^{-iH_0^{(S)}t}\right) -\left(e^{iH_0^{(S)}t}\,O(0)\,e^{-iH_0^{(S)}t}\right)H_0^{(S)}\right\}\notag\\ &=i\bigl[H_0^{(S)},O(t)\bigr]=i\bigl[H_0,O(t)\bigr] \tag{4.26} \end{align}
最後の等号が言えるのは \(H_0^{(S)}\) と \(H_0\) は一致するからである： \begin{equation*} H_0(t)=e^{iH_0^{(S)}t}H_0^{(S)}e^{-iH_0^{(S)}t}=e^{iH_0^{(S)}t}e^{-iH_0^{(S)}t}H_0^{(S)}=H_0^{(S)} \end{equation*}
もし \(H_I\) がゼロであれば, 式 (4.24) はハイゼンベルグ表示と同様に定常な状態ベクトルを与えること, そして式 (4.26) は \(H_0\) を全ハミルトニアン \(H\) に置き換えたハイゼンベルグ方程式に似ているのは面白いことである．\(H_0^{(S)}\) を \(H^{(S)}\) に置き換えると, 変換式 (4.23) は「シュレーディンガー表示」と「ハイゼンベルグ表示」を関連付けるおなじみの変換と同じになるので, このことはすべて予測できたはずある． \begin{align*} i\ppdiff{\Phi(t)}{t}&=0\ \rightarrow\ \Phi(t)=Const,\quad \frac{d}{dt}O(t)=i\bigl[H_0^{(S)},O(t)\bigr]\ \Leftrightarrow\ \frac{d}{dt}O^{(H)}=i\bigl[H^{(S)},O^{(H)}\bigr]\,.\\ \because\quad \Phi^{(H)}&=e^{iH^{(S)}t}\Phi^{(S)}=e^{-iH^{(S)}(-t)}\Phi^{(S)}(t)=\Theta(0,t)\Phi^{(S)}(t)=\Phi^{(S)}(0),\\ O^{(H)}&=e^{iH^{(S)}t}O^{(S)}e^{-iH ^{(S)}t} \end{align*} この3つの表示の違いをより系統的にまとめると次のようになる：
- 「ハイゼンベルグ表示」では, 状態ベクトルは完全に時間依存しないが, 他方, 時間依存する演算子はハイゼンベルグ方程式を満足する．
- 「シュレディンガー表示」では, 状態ベクトルが全ての時間依存性を担っている．
- 「相互作用表示」では, 時間依存性は2つの部分に分けられる．相互作用しない系(無摂動系)の時間依存性は演算子によって担われ[式(4.26)], 相互作用による時間依存性の残りの部分は状態ベクトルによって担われる[式(4.24)]．このため,「相互作用表示」は「中間表示」と呼ばれることもある．
量子場の理論では, 相互作用表示における場の演算子は, \(H_0\) のみを含む運動方程式 (4.26) を満足する．つまり相互作用がある場合でも, 相互作用表示を使えば場の演算子は「自由場」の方程式を満たすことになる．これまでの章で自由場の演算子の明示的な形式についてはすでに多くのことが分かっているので, これは実に喜ばしいことである．例えば, 電子の場では平面波展開の式 (3.392) を用いることが可能である． 相互作用ハミルトニアンはどうかと言うと, \(H_I\) は \(H_I^{(S)}\) と異なっており, \(H_I(t)\) に現れる場の演算子は, 時間依存する自由場の演算子 \(H_I^{(S)}(t)\) であることが特徴である：
\begin{equation*} H_I(t)=e^{iH_0^{(S)}t}\,H_I^{(S)}(t)\,e^{-iH_0^{(S)}t} \end{equation*}
\(U\)-行列と\(S\)-行列
そこで今度は, 微分方程式 (4.24) の形式解を求めてみよう．まず, 時間発展演算子 \(U(t,t_0)\) を次のように定義する：
\begin{equation} \Phi(t)=U(t,t_0)\Phi(t_0) \tag{4.27} \end{equation}
ただし \(\Phi(t_0)\) は, ある決まった時刻 \(t_0\) に於ける系を特徴付ける状態ベクトルである．明らかに次が言える： \begin{equation} U(t_0,t_0)=1 \tag{4.28} \end{equation}
方程式 (4.24) は次式と等価である： \begin{equation} i\pdiff{t}U(t,t_0)=H_I(t)U(t,t_0) \tag{4.29} \end{equation}
しかし, 微分方程式 (4.29) と境界条件 (4.28) は一緒になって, 次のような１個の積分方程式を与えることが出来る： \begin{equation} U(t,t_0)=1-i\int_{t_0}^{t}dt\,H_I(t)U(t,t_0) \tag{4.30} \end{equation}
これをよく知られた反復法で解いてみよう．すると次のようになる： \begin{align} U(t,t_0)&=1-i\int_{t_0}^{t}dt_1\,H_I(t_1)\left[1-i\int_{t_0}^{t_1}dt_2\,H_I(t_2)U(t_2,t_0)\right]\notag\\ &=1-i\int_{t_0}^{t}dt_1\,H_I(t_1)+(-i)^{2}\int_{t_0}^{t}dt_1\int_{t_0}^{t_1}dt_2\,H_I(t_1)H_I(t_2)+\dotsb\notag\\ &\quad +(-i)^{n}\int_{t_0}^{t}dt_1\int_{t_0}^{t_1}dt_2\dotsb\int_{t_0}^{t_{n-1}}dt_n\, H_I(t_1)H_I(t_2)\dotsb H_I(t_n)+\dotsb \tag{4.31} \end{align}
\(U\) の物理的な意味は次の通りである．系が \(t_0\) に於いて状態 \(i\) にあることが分かっているとする．後のある時刻 \(t\) で, 系が状態 \(f\) に在ることを発見する確率は次で与えられる： \begin{equation} \bigl|\BK{\Phi_f}{U(t,t_0)\Phi_i}\bigr|^{2}=\bigl|\BraKet{\Phi_f}{U(t,t_0)}{\Phi_i}\bigr|^{2} =\bigl|U_{fi}(t,t_0)\bigr|^{2} \tag{4.32} \end{equation}
\(i\to f\) の単位時間当たりの平均遷移確率は次となる： \begin{equation} w=\frac{1}{t-t_0}\bigl|U_{fi}(t,t_0)-\delta_{fi}\bigr|^{2} \tag{4.33} \end{equation}
なぜなら, 式 (4.31) の「\(1\)」は相互作用がない場合でも存在するからである．この比率は, 時間間隔 \(t-t_0\) が小さいときにはかなり複雑な時間依存性を持つが, \(t_0\to -\infty\) と \(t\to\infty\) で明確な極限に近づくことが, 次節で実際の物理問題を解くとき明快に分かるであろう．このことは「\(S\)-行列」と呼ばれるものを, 次のように定義する動機となる： \begin{equation} S=U(\infty,-\infty) \tag{4.34} \end{equation}
式 (4.27) から \(S\)-行列は \(\Phi(\infty)\) と \(\Phi(-\infty)\) を次式に従って結び付けることが分かる： \begin{equation} \Phi(\infty)=S\Phi(-\infty) \tag{4.35} \end{equation}
\(S\)-行列の明示的な形は式 (4.31) から容易に読み取る(推察する)ことが出来る： \begin{align} S&=S^{(0)}+S^{(1)}+S^{(2)}+S^{(3)}+\dotsb\notag\\ &=1-i\int_{-\infty}^{\infty}dt_1\,H_I(t_1)+(-i)^{2}\int_{-\infty}^{\infty}dt_1\int_{-\infty}^{t_1}dt_2\, H_I(t_1)H_I(t_2)+\dotsb \notag\\ &\quad +(-i)^{n}\int_{-\infty}^{\infty}dt_1\int_{-\infty}^{t_1}dt_2\dotsb\int_{-\infty}^{t_{n-1}}dt_n\, H_I(t_1)H_I(t_2)\dotsb H_I(t_n)+\dotsb \tag{4.36} \end{align}
(すなわち式 (4.34)：\(S=U(\infty,-\infty)\) から, 式 (4.31) の \(U(t,t_0)\) で \(t_0=-\infty,\,t=\infty\) としたものとなる)． 式 (4.36) の展開が有効かどうかは, 相互作用の強さに依存する．量子電気力学では \(S\)-行列の展開は急速に収束することが分かり, 最初の数項を考えるだけで観測と非常によく一致した結果を得ることが出来る．これは勿論, 無次元定数 \(\alpha\) が \(1\) に比べて小さいからである．しかし, 強い相互作用の物理分野では, 関連する(relevant) 展開パラメータが \(1\) のオーダーであるため, 状況はそれほど幸運ではない． ここで, 第2章で用いたDiracの時間依存摂動論と, ここで用いた形式との関連について考察しておくとよいだろう．まず, 係数 \(c_j(t)\) の時間発展を記述する式 (2.107) を見てみよう．\(c_j\) は本節でいうところの状態ベクトル \(\Phi\) に相当する列行列を形成していると考えてよい．すると, 微分方程式 (2.107) は式 (4.24) に正確に対応することが分かる： \begin{equation*} \frac{d}{dt}c_m(t)=\sum_k \frac{1}{i\hbar}\BraKet{m}{H_I(t)}{k} e^{i(E_m-E_k)t/\hbar} c_k(t) \tag{2.107} \end{equation*}
係数 \(c_j(t)\) は初期状態 \((k)\) と最終状態 \((j)\) の間の展開式 (4.31) の行列要素に他ならない： \begin{align*} c_j(t)&=\BraKet{j}{U(t,t_0)}{k}\\ &=\BK{j}{k}-i\int_{t_0}^{t}dt_1\,\BraKet{j}{H_I(t_1)}{k}+(-i)^{2}\int_{t_0}^{t}dt_1\int_{t_0}^{t_1}dt_2\, \BraKet{j}{H_I(t_1)H_I(t_2)}{k}+\dotsb\\ &\quad +(-i)^{n}\int_{t_0}^{t}dt_1\int_{t_0}^{t_1}dt_2\dotsb\int_{t_0}^{t_{n-1}}dt_n\, \BraKet{j}{H_I(t_1)H_I(t_2)\dotsb H_I(t_n)}{k}+\dotsb \end{align*} そして \(c_j(0)=\delta_{jk}\) は, 式 (4.31) の第１項に対応し, 式 (2.109) で与えられる \(c^{(1)}_j(t)\) は展開式 (4.31) に於いて \(t_0=0\) とした第2項に対応することが, \begin{equation} \BraKet{j}{H_I(t)}{k}=\BraKet{j}{e^{iH_0 t}H_I^{(S)}e^{-iH_0 t}}{k}=\BraKet{j}{H_I^{(S)}}{k}e^{i(E_j-E_k)t} \tag{4.37} \end{equation}
を思い出すことで容易に理解できる： \begin{align*} c_j(0)&=\BraKet{j}{U_I(t=0,t_0=0)}{i}=\BraKet{j}{U(t_0,t_0)}{i}=\BK{j}{i}=\delta_{ji},\tag{4.31′-a}\\ c_m^{(1)}(t)&=\frac{1}{i\hbar}\int_{0}^{t}dt’\,\BraKet{m}{H_I(t’)}{n}e^{i(E_m-E_n)t’/\hbar},\tag{2.109}\\ \rightarrow\ c_j^{(1)}(t)&=\frac{1}{i\hbar}\int_{t_0=0}^{t}dt’\,\BraKet{j}{H_I^{(S)(t’)}}{i}e^{i(E_j-E_i)t/\hbar} =-\frac{i}{\hbar}\int_0^{t}dt’\,\BraKet{j}{H_I(t’)}{i}\tag{4.31′-b} \end{align*} 高次の項についても同様のことが言える．この観点から言えば,相互作用表示の基本的な考え方はDiracの時間依存摂動論と同じくらい古いものである．[1][訳註] 本文の式 (2.103) で定義される係数 \(c_k(t)\) は, ファインマン本の § 8-9 では振幅「\(G_{mn}\)」として, 式 (8-137) で定義され, また, 振幅 \(G_{mn}\) … Continue reading
しかし, 非相対論的量子力学で学ぶ摂動法と本章で展開する摂動法とは重要な違いがある．非相対論では式 (4.37) を用いて, まず式 (4.36) の \(t_1,\,t_2\) などを積分して, 次のような式で規定される「遷移行列」\(T_{fi}\)を得る：
\begin{align} S_{fi}&=\delta_{fi}-2\pi i \delta(E_f-E_i)\,T_{fi},\tag{4.38}\\ T_{fi}&=H_{fi}^{(S)}+\sum_n \frac{H_{fi}^{(S)}H_{ni}^{(S)}}{E_i-E_n + i\epsilon}+\dotsb \tag{4.39} \end{align}
(ただし簡単化のために \(H^{(S)}\) は時間に依存しないと仮定している)[2][訳註] J.J.Sakuraiの § 5-6 では係数 \(c^{(1)}_m(t)\) は次の式 (5.6.17) で定義され, ファインマンの§ 6-5 で定義されている 1 次の遷移振幅 \(\lambda_{mn}^{(1)}\) … Continue reading． そしてその後, 次のような空間積分 \begin{equation} H_{fn}^{(S)}=\frac{1}{V}\int e^{-i\mb{p}_f\cdot\mb{x}}H^{(S)}e^{i\mb{p}_n\cdot\mb{x}}\,d^{3}\mb{x} \tag{4.40} \end{equation}
などを行う．この章では, そのような進め方はしない．代わりに, 共変的に空間積分と時間積分を同時に行うことを提案する．その結果, 基本式 (4.24) も, 相互作用ハミルトニアン \begin{equation} H_I=\int {\large\mathscr{H}}_{\mathrm{int}}\,d^{3}x \tag{4.41} \end{equation}
も共変的でないにもかかわらず,「遷移行列」に対しては明らかに共変的な式を得ることが可能になる．この方法がどのように機能するかは, 次節以降で見ていくことにしよう．
ユニタリー性(Unitarity)
最後に, \(S\)-行列の「ユニタリー性」について述べて本節を終える：
\begin{equation} S\,S^{\!\dagger}=1,\qquad S^{\!\dagger}\,S=1 \tag{4.42} \end{equation}
または等価的には, \begin{align} &\sum_n S_{fn}(S^{\!\dagger}\,)_{ni}=\sum_n S_{fn}S_{in}^{*}=\delta_{fi},\tag{4.43a}\\ &\sum_n S_{nf}^{*}S_{ni}=\delta_{fi} \tag{4.43b} \end{align}
この重要な性質を証明する方法はいくつかあるが, ここでは \(S\)-行列の展開式 (4.36) の明示的な形式に基づく直接的な証明(2次までの)を紹介する．\(H_I\) はある結合パラメータ \(\lambda\) に線形であると仮定する；例えば, \begin{equation*} H_I=-ie\int \overline{\varPsi}\,\ \gamma_{\mu}\,\varPsi A_{\mu}\,d^{3}x \end{equation*}
の場合は \(\lambda=e\) で, パラメータ \(\lambda\) は \(e\) そのものである．\(S^{(0)}\) は \(\lambda^{0}=1\) として, \(S^{(1)}\) は \(\lambda^{1}\)として, \(S^{(2)}\) は \(\lambda^{2}\) として変化する,等々．一方, ユニタリー方程式 (4.43) は次のように書くことが出来る： \begin{equation} \sum_n \big(S_{fn}^{(0)}+S_{fn}^{(1)}+S_{fn}^{(2)}+\dotsb\big) \big(S_{in}^{(0)*}+S_{in}^{(1)*}+S_{in}^{(2)*}+\dotsb\big)=\delta_{fi} \tag{4.44} \end{equation}
上式は, どんな値の \(\lambda\) に対しても恒等式の関係として成立するはずである．よって, 式 (4.44) 左辺の \(\lambda\) の各次数についてその係数は皆, ユニタリー関係を満たすためにはゼロになければならない．従って, 各次数について次が成り立つべきである： \begin{align} &\lambda^{0}:\quad \sum_{n}S_{fn}^{(0)}S_{in}^{(0)*}=\delta_{fi},\ \mathrm{or}\ \sum_{n}S_{fn}^{(0)}S_{in}^{(0)*}-\delta_{fi}=0,\tag{4.45a}\\ &\lambda^{1}:\quad \sum_{n} \bigl(S_{fn}^{(0)}S_{in}^{(1)*}+S_{fn}^{(1)}S_{in}^{(0)*}\bigr)=0,\tag{4.45b}\\ &\lambda^{2}:\quad \sum_{n} \bigl(S_{fn}^{(0)}S_{in}^{(2)*}+S_{fn}^{(2)}S_{in}^{(0)*}\bigr) +\sum_{n}S_{fn}^{(1)}S_{in}^{(1)*}=0,\tag{4.45c}\\ &\qquad \qquad\qquad \vdots\notag \end{align}
最初の式 (4.45a) が成り立つのは自明である．なぜなら, 次が言えるからである： \begin{equation} S_{fn}^{(0)}=\BraKet{f}{U(t_0,t_0)}{n}=\BraKet{f}{1}{n}=\BK{f}{n}=\delta_{fn}, \qquad S_{in}^{(0)*}=\delta_{in} \tag{4.46} \end{equation}
式 (4.46) の理由で, 今やオーダー \(\lambda^{1}\)のユニタリー関係式 (4.45b) は, 式 (4.36) による \(S^{(1)}\) を用いて次となる： \begin{align} S^{(1)}=-i\int_{-\infty}^{\infty}dt\,H_I(t)\ \rightarrow&\ S^{(1)}_{fi}=-i\int_{-\infty}^{\infty}dt\,\BraKet{f}{H_I(t)}{i},\quad S^{(1)*}_{if}=i\int_{-\infty}^{\infty}dt\,\BraKet{i}{H_I(t)}{f}^{*},\notag\\ \sum_{n} \bigl(S_{fn}^{(0)}S_{in}^{(1)*}+S_{fn}^{(1)}S_{in}^{(0)*}\bigr) &=\sum_n\delta_{fn}S_{in}^{(1)*}+\sum_nS_{fn}^{(1)}\delta_{in}=S_{if}^{(1)*}+S_{fi}^{(1)}\notag\\ &=i\int_{-\infty}^{\infty}dt\,\BraKet{i}{H_I(t)}{f}^{*}-i\int_{-\infty}^{\infty}dt\,\BraKet{f}{H_I(t)}{i},\notag\\ \therefore\quad i\int_{-\infty}^{\infty}dt\,&\BraKet{i}{H_I(t)}{f}^{*}-i\int_{-\infty}^{\infty}dt\,\BraKet{f}{H_I(t)}{i}=0, \tag{4.47}\\ \mathrm{or},\quad \int_{-\infty}^{\infty}dt&\,\BraKet{i}{H_I(t)}{f}^{*} =\int_{-\infty}^{\infty}dt\,\BraKet{f}{H_I(t)}{i}\notag \end{align}
この関係は \(H_I\) が「エルミート」すなわち \(H_I^{\dagger}=H_I\) であれば満たされる： \begin{equation*} (H^{\dagger}_I)_{jk}=(H_I)^{*}_{kj}=(H_I)_{jk}\ \rightarrow\ \BraKet{i}{H_I(t)}{f}^{*}=\BraKet{f}{H_I(t)}{i} \end{equation*}
式 (4.45c) の証明する前に, 次の \(S^{(2)}\) に対する非常に重要な等価式を証明しなければならない： \begin{align} S^{(2)}&=(-i)^{2}\int_{-\infty}^{\infty}dt_1\int_{-\infty}^{t_1}dt_2\,H_I(t_1)H_I(t_2)\ :\ \mathrm{Form}\,1\notag\\ &=(-i)^{2}\int_{-\infty}^{\infty}dt_1\int^{\infty}_{t_1}dt_2\,H_I(t_2)H_I(t_1)\,\ :\ \mathrm{Form}\, 2 \tag{4.48} \end{align}
これを証明するために, 最初の式を積分変数の交換 \(t_1\leftrightarrow t_2\) をした形に書き直してみる (単なる変数名の書き換え)： \begin{equation} S^{(2)}=(-i)^{2}\int_{-\infty}^{\infty}dt_2\int_{-\infty}^{t_2}dt_2\,H_I(t_2)H_I(t_1) \tag{4.49} \end{equation}
このとき \(t_2\) は固定して \(t_1\) について \(-\infty\) から \(t_2\) まで積分し, 次に \(t_2\) について \(-\infty\) から \(\infty\) まで積分することになっている．つまり, ２次元の \(t_1 t_2\) 平面では, 図 4-1(a) に示すように, 直線 \(t_2=t_1\) の上の領域で \(H_I(t_2)H_I(t_1)\) を積分しなければならないことになる．しかし, 図 4-1(b) から明らかなように, 式 (4.49) は等価的に次のように書くことが出来る： \begin{equation} S^{(2)}=(-i)^{2}\int_{-\infty}^{\infty}dt_1\int^{\infty}_{t_1}dt_2\,H_I(t_2)H_I(t_1) \tag{4.50} \end{equation}
これは式 (4.48) の第2番目の式の形になっており, 従って証明された．式 (4.48) の最初と2番目の式形は \(S^{(2)}\) の「第1形式」(Form 1)及び「第2形式」(Form 2)と呼ぶことにする．
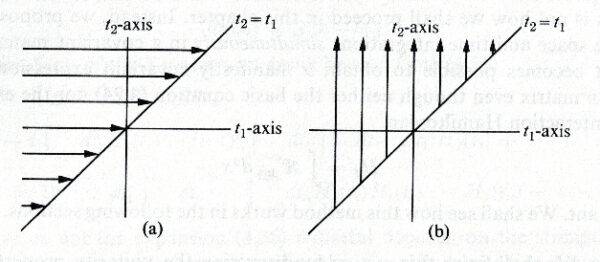
図 1. 式 (4.49) と式 (4.50) の積分範囲．
この \(S^{(2)}\) の重要な恒等式とすでに示した式 (4.47) を用いて, 式 (4.45c) から \(\lambda\) の2次までのユニタリー性関係を証明するには, 次のことを証明すればよいことが分かる：
\begin{align} &\sum_n \int_{-\infty}^{\infty}dt\,\BraKet{f}{H_I(t)}{n}\int_{-\infty}^{\infty}dt\,\BraKet{n}{H_I(t)}{i}\notag\\ &=-(-i)^{2}\left[\int_{-\infty}^{\infty}dt_1\int_{t_1}^{\infty}dt_2\BraKet{i}{H_I(t_2)H_I(t_1)}{f}^{*} +\int_{-\infty}^{\infty}dt_1\int_{-\infty}^{t_1}dt_2\BraKet{f}{H_I(t_1)H_I(t_2)}{i}\right] \tag{4.51} \end{align}
ただし式 (4.45c) の \(S_{in}^{(2)*}\) には (Form 2) を, そして \(S_{fn}^{(2)}\) には (Form 2) を用いている．\(H_I(t)\) のエルミート性を用い, 中間状態の完全性関係 \(\sum_n\ket{n}\bra{n}=1\) を \(H_I(t_1)\) と \(H_I(t_2)\) の間に挿入するならば, 式 (4.51) の右辺は簡単化されて次式になることは容易に分かることである： \begin{equation} \sum_n \int_{-\infty}^{\infty}dt_1\,\left[\int_{t_1}^{\infty}dt_2+\int_{-\infty}^{t_1}dt_2\right] \BraKet{f}{H_I(t_1)}{n}\BraKet{n}{H_I(t_2)}{i} \tag{4.52} \end{equation}
これは式 (4.51) の左辺と同じである．この方法は容易に一般化することが出来るので, 式 (4.43a) の意味で \(S\)-行列は全ての(有限な)オーダーでユニタリーであることが証明される．式 (4.43b) に対しても, 同様な証明を実行することが出来る． 先ほど２次まで検証したユニタリー性の物理的な意味を理解するために, 前に与えた \(U\)-行列の確率論的な解釈に戻ることにしよう．\(t = -\infty\) のとき, 系が状態 \(i\) にあることが確実であると仮定しよう．式 (4.32) によれば, \(t =\infty\) に於いて系がある特定の終状態 \(f\) に在ることを見出す確率は \(|S_{fi}|^{2}\) で与えられる．「全ての可能な」終状態を考えるとき, \(t =\infty\) での確率の和は \(1\) にならなければならない： \begin{equation} \sum_f |S_{fi}|^{2}=1 \tag{4.53} \end{equation}
この必要条件は「\(S\)-行列がユニタリーである」場合に保証される．第3章で強調したように, 相対論的量子力学では粒子が自由に生成・消滅するため, 与えられた1つの粒子を観測する確率の密度を全空間で積分したものは, もはや一定ではなくなる．例えば, 運動量 \(\mb{p}\) と \(-\mb{p}\) を持った \(e^{+} + e^{-}\) から始めると, 終状態は \(\mb{p}’\) と \(-\mb{p}’\) を持った \(e^{+} + e^{-}\) だけでなく, \(2\gamma,\,3\gamma\), \(e^{+}+e^{-}+\gamma\) などの可能性がある．しかし, もし和 \(f\) に含めるのは「始状態がエネルギー保存的な遷移をすることができるすべての状態」とするならば, 式 (4.53) の意味での確率保存は依然として成立しているのである．[3][訳註] 前述の式 (4.38) は \(S\)-行列要素を遷移行列 \(T_{fi}\) で表した式であるが, そこにはデルタ関数
\(\delta(E_f-E_i)\) … Continue reading
\(S\)-行列のユニタリー性関係を証明する上で, 相互作用ハミルトニアンのエルミート性が果たす役割を強調したい．逆に, 式 (4.47) を根拠に, 量子論における確率保存は「相互作用密度をエルミート演算子とすること」を要求していると主張することも出来る．実際, 確率保存性やユニタリー性の要請を議論の出発点とすることも出来る．\(S^{(1)}\) が \(H_I\) の時間積分の \(-i\) 倍で与えられるとすると, ユニタリー性を満たすためには \(S^{(2)}\) はどうあるべきかを問うことが出来るであろう．このように, ハミルトン形式から \(S\)-行列の展開を導くのではなく, \(S\)-行列のユニタリー性要件と他の幾つかの一般原理から \(S\)-行列の展開を導くことが出来る．この方法は, 特に N.N.Bogoliubov とその共同研究者によって提唱されたもので, 興味深い別の視点であるが, これ以上の議論はしないことにする．[4] Bogoliubov and Shirkov(1959),pp.206-226. を参照せよ． ユニタリー性関係を式 (4.38) で定義される \(T\)-行列の観点から言うと次のようになる：[5][訳註] 式 (4.54) を示しておく．行列 \(U\) のユニタリー性 \(U^{\dagger}U=1\) を成分で表すならば次となる： \[\sum_k U_{ik}^{\dagger}U_{kj}=\sum_k … Continue reading
\begin{equation} i(T_{fi}-T_{if}^{*})=2\pi\sum_n \delta(E_f-E_n)T^{*}_{nf}T_{ni} \tag{4.54} \end{equation}
この関係から, 全断面積と前方散乱振幅の虚部との関係を述べた「光学的定理」を導くことが出来る(式(2.219)を参照)．[6][訳註] 「光学定理」とは,前方散乱振幅\(f(\theta=0)\)の虚数部分を,全断面積\(\sigma_{tot}\)と関連付ける定理である： \begin{equation*} \mathrm{Im}\,f(\theta=0) = … Continue reading この重要な定理の式 (4.54) からの導出は, 現代の非相対論的量子力学の教科書のほとんどで扱われているのでここでは割愛する． Merzbacher (1961), pp. 495-499; Messiah (1962), p. 866. を参照せよ． ユニタリー性の原理のやや異なる応用については第4-7節で議論する．そこでは, 真空分極を外場による対生成に関係付けるのに, 式 (4.45c) がどのように用いられるかを提示するであろう．References
| ↑1 | [訳註] 本文の式 (2.103) で定義される係数 \(c_k(t)\) は, ファインマン本の § 8-9 では振幅「\(G_{mn}\)」として, 式 (8-137) で定義され, また, 振幅 \(G_{mn}\) と「遷移振幅」\(\lambda_{mn}\) と次の関係にあった(前のブログ記事を参照)： \begin{align*} &\psi=\sum_k c_k(t)u_k(\mb{x})e^{-iE_k t/\hbar},\quad G_{mn}=\BraKet{m}{U_I(t,t_0)}{n}=e^{iE_m T/\hbar}\BraKet{\psi_m}{U(T,0)}{\psi_n}=c_m(t),\\ &c_m(t)=G_{mn}=\BraKet{m}{U_I(t,t_0)}{n}=e^{i(E_m t -E_n t_0)/\hbar}\,\BraKet{\psi_m}{U_I(t,t_0)}{\psi_n}=e^{i(E_m t -E_n t_0)/\hbar}\,\lambda_{mn} \end{align*} 従って, 式 (4.32) の「遷移確率」は次のように表わすことが出来る： \begin{equation*} \bigl|G_{fi}\bigr|^{2}=\bigl|\BraKet{f}{U_I(t,t_0)}{i}\bigr|^{2} =\bigl|\BraKet{\Phi_f}{U_I(t,t_0)}{\Phi_n}\bigr|^{2}=\bigl|U_{fi}(t,t_0)\bigr|^{2} \end{equation*} また, \(S^{(1)}_{fi}\) と \(c_{f}^{(1)}(t)\) や \(S^{(2)}_{fi}\) と \(c_{f}^{(2)}(t)\) の関係, すなわち \(S_{fi}\) と \(c_f(t)\) の関係は次となるであろう： \begin{align*} c_{f}(t)&=\BraKet{f}{U_I(t,t_0)}{i},\quad S_{fi}=\BraKet{f}{U_I(\infty,-\infty)}{i},\quad \rightarrow\quad S_{fi}=\lim_{\substack{t\to +\infty \\ t_0\to -\infty}}c_{f}(t)\\ c_{f}^{(1)}(t)&=-i\int_{t_0}^{t}dt’\,\BraKet{f}{H_I(t’)}{i},\quad S_{fi}^{(1)}=-i\int_{-\infty}^{\infty}dt\,\BraKet{f}{H_I(t)}{i},\\ c_{f}^{(2)}(t)&=(-i)^{2}\int_{t_0}^{t}dt_1\int_{t_0}^{t_1}dt_2\,\BraKet{f}{H_I(t_1)H_I(t_2)}{i},\ S_{fi}^{(2)}=(-i)^{2}\int_{-\infty}^{\infty}dt_1\int_{-\infty}^{t_1}dt_2\,\BraKet{f}{H_I(t_1)H_I(t_2)}{i},\\ \rightarrow &\quad S_{fi}^{(1)}=\lim_{\substack{t\to +\infty \\ t_0\to -\infty}}c_{f}^{(1)}(t),\quad S_{fi}^{(2)}=\lim_{\substack{t\to +\infty \\ t_0\to -\infty}}c_{f}^{(2)}(t),\quad \dotsb\quad \therefore\quad S_{fi}=\lim_{\substack{t\to +\infty \\ t_0\to -\infty}}c_{f}(t) \end{align*} |
|---|---|
| ↑2 | [訳註] J.J.Sakuraiの § 5-6 では係数 \(c^{(1)}_m(t)\) は次の式 (5.6.17) で定義され, ファインマンの§ 6-5 で定義されている 1 次の遷移振幅 \(\lambda_{mn}^{(1)}\) 及び § 8-9 で定義されている \(G_{mn}\) は次であった： \begin{align*} c_m^{(1)}(t)&=\BraKet{m}{U_I(t,t_0)}{n}=-\frac{i}{\hbar}\int_{t_0}^{t}\BraKet{m}{V_I(t’)}{n}\,dt’ =\frac{1}{i\hbar}\int_{t_0}^{t}dt’\BraKet{m}{V(t’)}{n}e^{i(E_m-E_n)t’/\hbar},\tag{5.6.17}\\ \lambda_{mn}^{(1)}&=-\frac{i}{\hbar}\int_{t_0}^{t}dt_3\int_{-\infty}^{\infty}dx_3\, \phi_m^{*}(x_3)V(x_3,t_3)\phi_n(x_3)\,e^{(i\{E_m(t_3-t_2)-E_n(t_3-t_1)\}/\hbar}\tag{6-70}\\ &=-\frac{i}{\hbar}\int_{t_0}^{t}dt_3\,V_{mn}(t_3)\,e^{i\{E_m(t_3-t_2)-E_n(t_3-t_1)\}/\hbar} =e^{-i(E_m t_2-E_n t_1)/\hbar}\,G_{mn},\\ G_{mn}&=e^{i(E_m t_b-E_n t_a)/\hbar}\int_{-\infty}^{\infty}dx_b\int_{-\infty}^{\infty}dx_a\, \phi^{*}_m(x_b)K(x_b,t_b;x_a,t_a)\phi_n(x_a)\tag{8-137}\\ &=e^{i(E_m t_b-E_n t_a)/\hbar}\int_{-\infty}^{\infty}dx_b\,\phi^{*}_m(x_b)\psi(x_b) =e^{i(E_m t_b-E_n t_a)/\hbar}\lambda_{mn}=c_m^{(1)}(t_3) \end{align*} 他方, ここで定義される \(S\)-行列または \(S_{mn}\) は \(S_{mn}=\BraKet{m}{U_I(\infty,-\infty)}{n}\) であった．従って, 式 (5.6.17) より, \begin{equation*} S^{(1)}_{mn}=\lim_{\substack{t\to +\infty \\ t_0\to -\infty}}c_{m}^{(1)}(t) =-\frac{i}{\hbar}\int_{-\infty}^{\infty}\BraKet{m}{V(t’)}{n}e^{i(E_m-E_n)t’/\hbar}\,dt’ \end{equation*} ここで摂動 \(V(t’)\) が時間に依存しないと仮定すると, その行列要素は積分の外へだせるので, \begin{equation*} S_{mn}^{(1)}=-\frac{i}{\hbar}\BraKet{m}{V}{n}\int_{-\infty}^{\infty}e^{i(E_m-E_n)t’/\hbar}\,dt’ \tag{1} \end{equation*} この式中の積分はデルタ関数と見做すことが出来る．また, デルタ関数の性質 \(\delta(ax)=\delta(x)/a\) を用いると, \begin{equation*} \delta(x)=\frac{1}{2\pi}\int_{-\infty}^{\infty}e^{ikx}\,dk\quad \rightarrow\quad \int_{-\infty}^{\infty}e^{i(E_m-E_n)t’/\hbar}\,dt’=2\pi\hbar\,\delta(E_m-E_n) \end{equation*} 従って, 上式 (1) は, \begin{equation*} S_{mn}^{(1)}=-\frac{i}{\hbar}\BraKet{m}{V}{n}\times 2\pi \hbar\,\delta(E_m-E_n)=-i2\pi\,\delta(E_m-E_n)\BraKet{m}{V}{n} \end{equation*} よって \(S\)-行列を 1 次までに近似するならば,「遷移行列」を \(T_{mn}=\BraKet{m}{V}{n}\) として次が言える： \begin{equation*} S_{mn}=\delta_{mn}-2\pi i\,\delta(E_m-E_n)\BraKet{m}{V}{n} =\delta_{mn}-2\pi i\,\delta(E_m-E_n)T_{mn} \end{equation*} |
| ↑3 | [訳註] 前述の式 (4.38) は \(S\)-行列要素を遷移行列 \(T_{fi}\) で表した式であるが, そこにはデルタ関数 \(\delta(E_f-E_i)\) が入っている．これはエネルギー保存的に遷移できる場合だけを含めることを表しているのである． |
| ↑4 | Bogoliubov and Shirkov(1959),pp.206-226. を参照せよ． |
| ↑5 | [訳註] 式 (4.54) を示しておく．行列 \(U\) のユニタリー性 \(U^{\dagger}U=1\) を成分で表すならば次となる： \[\sum_k U_{ik}^{\dagger}U_{kj}=\sum_k U_{ki}^{*}U_{kj}=\delta_{ij}\] これを \(S\)-行列に当てはめ, 式 (4.38) を用いるならば, \begin{align*} &S_{ni}=\delta_{ni}-2\pi i\delta(E_n-E_i)T_{ni},\quad S^{*}_{nf}=\delta_{nf}+2\pi i\delta(E_n-E_f)T_{nf}^{*},\\ &\sum_n S^{\dagger}_{fn}S_{ni}=\sum_n S^{*}_{nf}S_{ni}=\delta_{fi},\\ &\sum_n S^{*}_{nf}S_{ni}=\sum_n \left(\delta_{nf}+2\pi i\delta(E_n-E_f)T_{nf}^{*}\right)\times \left(\delta_{ni}-2\pi i\delta(E_n-E_i)T_{ni}\right)\\ &\quad=\sum_n \delta_{nf}\delta_{ni}-2\pi i\sum_n \delta_{nf}\delta(E_n-E_i)T_{ni} +2\pi i \sum_n \delta_{ni}\delta(E_n-E_f)T_{nf}^{*}\\ &\qquad +(2\pi)^{2}\sum_n \delta(E_n-E_f)\delta(E_n-E_i)T_{ni}T_{nf}^{*}\\ &\quad =\delta_{fi}-2\pi i\delta(E_f-E_i)T_{fi}+2\pi i\delta(E_i-E_f)T_{if}^{*} +(2\pi)^{2}\sum_n \delta(E_n-E_f)\delta(E_f-E_i)T_{ni}T_{nf}^{*}=\delta_{fi},\\ &\therefore\quad -2\pi i\delta(E_f-E_i)T_{fi}+2\pi i\delta(E_i-E_f)T_{if}^{*} +(2\pi)^{2}\sum_n \delta(E_n-E_f)\delta(E_f-E_i)T_{ni}T_{nf}^{*}=0 \end{align*} 全体を \(-2\pi\delta(E_f-E_i)\) で割り算すれば目的の式 (4.54) となる： \begin{equation*} iT_{fi}-iT_{if}^{*}-2\pi\sum_n \delta(E_f-E_n)T_{ni}T_{nf}^{*}=0 \end{equation*} |
| ↑6 | [訳註] 「光学定理」とは,前方散乱振幅\(f(\theta=0)\)の虚数部分を,全断面積\(\sigma_{tot}\)と関連付ける定理である： \begin{equation*} \mathrm{Im}\,f(\theta=0) = \frac{k}{4\pi}\sigma_{tot} \end{equation*} ただし\(f(\theta=0)\equiv f(\mb{k},\mb{k})\)であり,また, \(\displaystyle{\sigma_{tot}=\int \frac{d\sigma}{d\Omega}\,d\Omega,\ \frac{d\sigma}{d\Omega}=|f(\mb{k}’,\mb{k})|^{2}}\) である． |
