\(\textit{Third Lecture}\)
平面波の光子を次のポテンシャルで表現することは, 本質的には「ゲージ」の選択である.選択の自由が存在することは, パウリ方程式が量子力学的なゲージ変換に対して不変であることに起因している.
量子力学的なゲージ変換は, 以下の古典的なゲージ変換を単純に拡張したものである:[1][ 訳註 ] ファインマンはゲージ変換の式 (3.1)\(\sim\)(3.4) を次のように記している:
if \(\mathbf{E}=-\nabla \phi +\partial\phi/\partial t\) and … Continue reading
\begin{align}
\def\ppdiff#1#2{\frac{\partial #1}{\partial #2}}
\def\pdiff#1{\frac{\partial}{\partial #1}}
\def\mb#1{\mathbf{#1}}
\def\reverse#1{\frac{1}{#1}}
\def\ds#1{\mbox{${\displaystyle\strut #1}$}}
\mb{E}&=-\nabla \phi -\frac{1}{c}\ppdiff{\mb{A}}{t},\tag{3.1}\\
\mb{B}&=\nabla\times\mb{A}\tag{3.2}
\end{align}
\def\ppdiff#1#2{\frac{\partial #1}{\partial #2}}
\def\pdiff#1{\frac{\partial}{\partial #1}}
\def\mb#1{\mathbf{#1}}
\def\reverse#1{\frac{1}{#1}}
\def\ds#1{\mbox{${\displaystyle\strut #1}$}}
\mb{E}&=-\nabla \phi -\frac{1}{c}\ppdiff{\mb{A}}{t},\tag{3.1}\\
\mb{B}&=\nabla\times\mb{A}\tag{3.2}
\end{align}
そして \(\chi\) を任意のスカラーとするならば, 次式を代入しても \(\mb{E}\) と \(\mb{B}\) は不変である:
\begin{align}
\mb{A}’&=\mb{A}+\nabla\chi,\tag{3.3}\\
\phi’&=\phi-\frac{1}{c}\ppdiff{\chi}{t}\tag{3.4}
\end{align}
\mb{A}’&=\mb{A}+\nabla\chi,\tag{3.3}\\
\phi’&=\phi-\frac{1}{c}\ppdiff{\chi}{t}\tag{3.4}
\end{align}
量子力学では, さらに次のような波動関数の変換が導入される:
\begin{equation}
\psi’=\exp\left(i\frac{e}{\hbar c}\chi\right)\,\psi\tag{3.5}
\end{equation}
\psi’=\exp\left(i\frac{e}{\hbar c}\chi\right)\,\psi\tag{3.5}
\end{equation}
これによるパウリ方程式の不変性は以下のようにして示される.パウリ方程式は,
\begin{equation}
-\frac{\hbar}{i}\ppdiff{\psi}{t}=\frac{1}{2m}\left[\mb{\sigma}\cdot\left(
\mb{p}-\frac{e}{c}\mb{A}\right)\right]\left[\mb{\sigma}\cdot\left(
\mb{p}-\frac{e}{c}\mb{A}\right)\right]\psi+e\,\phi\,\psi
\tag{3.6}
\end{equation}
-\frac{\hbar}{i}\ppdiff{\psi}{t}=\frac{1}{2m}\left[\mb{\sigma}\cdot\left(
\mb{p}-\frac{e}{c}\mb{A}\right)\right]\left[\mb{\sigma}\cdot\left(
\mb{p}-\frac{e}{c}\mb{A}\right)\right]\psi+e\,\phi\,\psi
\tag{3.6}
\end{equation}
すると, [\(\mb{p}=-i\hbar\nabla\) として]
\begin{align*}
\pdiff{\mb{x}}\psi’ &=\pdiff{\mb{x}}\exp\left(i\frac{e}{\hbar c}\chi\right)\psi
= \exp\left(i\frac{e}{\hbar c}\chi\right)\ppdiff{\psi}{\mb{x}}+i\frac{e}{\hbar c}\ppdiff{\chi}{\mb{x}}
\psi \exp\left(i\frac{e}{\hbar c}\chi\right),\\
\mb{p}\exp\left(i\frac{e}{\hbar c}\chi\right)
&=-i\hbar\nabla\,\exp\left(i\frac{e}{\hbar c}\chi\right)
=-i\hbar\left(i\frac{e}{\hbar c}\right)\nabla \chi\,\exp\left(i\frac{e}{\hbar c}\chi\right)
=\exp\left(i\frac{e}{\hbar c}\chi\right)\frac{e}{c}\nabla\chi,\\
\rightarrow\ \mb{p}\left\{\exp\left(i\frac{e}{\hbar c}\chi\right)\psi\right\}
&=\left\{\mb{p}\exp\left(i\frac{e}{\hbar c}\chi\right)\right\}\psi + \exp\left(i\frac{e}{\hbar c}\chi\right)\mb{p}\psi
=\exp\left(i\frac{e}{\hbar c}\chi\right)\left(\mb{p}+\frac{e}{c}\nabla\chi\right)\psi
\end{align*}
そして,
\begin{align*}
\left(\mb{p}-\frac{e}{c}\mb{A}\right)\exp\left(i\frac{e}{\hbar c}\chi\right)\psi
&=\mb{p}\left\{\exp\left(i\frac{e}{\hbar c}\chi\right)\psi\right\}
-\frac{e}{c}\mb{A}\exp\left(i\frac{e}{\hbar c}\chi\right)\psi\\
&=\exp\left(i\frac{e}{\hbar c}\chi\right)\left(\mb{p}+\frac{e}{c}\nabla\chi \right)\psi-\exp\left(i\frac{e}{\hbar c}\chi\right)\frac{e}{c}\mb{A}\psi\\
&=\exp\left(i\frac{e}{\hbar c}\chi\right)\left(\mb{p} -\frac{e}{c}\mb{A}+\frac{e}{c}\nabla\chi\right)\psi
\end{align*}
時間についての偏微分は, 項 \(\displaystyle{\left(-\frac{e}{c}\ppdiff{\chi}{t}\right)\exp\left(i\frac{e}{\hbar c}\chi\right)\psi}\) をもたらし, これは \(\displaystyle{e\,\phi\cdot\exp\left(i\frac{e}{\hbar c}\chi\right)\psi}\) に含まれるとして良い.
従って, 次の代入を行っても Pauli 方程式は変わらない: [2][ 訳註 ] 【 参考 】 (A) \(\phi\) をスカラー量とするとき「\(\nabla\times\nabla\phi=0\)」となる.このベクトル解析の重要な公式が成り立つことは, … Continue reading
\begin{equation}
\psi’=\exp\left(i\frac{e}{\hbar c}\chi\right)\,\psi,\quad \mb{A}’=\mb{A}+\nabla\chi,\quad
\phi’=\phi -\frac{1}{c}\ppdiff{\chi}{t}
\tag{3.7}
\end{equation}
\psi’=\exp\left(i\frac{e}{\hbar c}\chi\right)\,\psi,\quad \mb{A}’=\mb{A}+\nabla\chi,\quad
\phi’=\phi -\frac{1}{c}\ppdiff{\chi}{t}
\tag{3.7}
\end{equation}
光子に対して定義されるベクトルポテンシャル \(\mb{A}\) は, 状態 \(i\) から状態 \(f\) への遷移の摂動ポテンシャルとしてパウリ・ハミルトニアンに加わる.次式で書かれる時間依存する摂動
\begin{equation}
\Delta H = e^{i\omega t}U(x,y,z)
\tag{3.8}
\end{equation}
\Delta H = e^{i\omega t}U(x,y,z)
\tag{3.8}
\end{equation}
は皆, 次の行列要素 \(U_{fi}\) に帰着する:
\begin{align}
U_{fi}&=\int\psi^{*}_f \,\Delta H \,\psi_i\,dVol\notag\\
&=\int \phi_f^{*}(x)\exp(iE_f t/\hbar)e^{i\omega t}\,U(\mb{x})\exp(-iE_i t/\hbar)
\phi_i(\mb{x})\,dVol
\tag{3.9}
\end{align}
U_{fi}&=\int\psi^{*}_f \,\Delta H \,\psi_i\,dVol\notag\\
&=\int \phi_f^{*}(x)\exp(iE_f t/\hbar)e^{i\omega t}\,U(\mb{x})\exp(-iE_i t/\hbar)
\phi_i(\mb{x})\,dVol
\tag{3.9}
\end{align}
この式は「その摂動は, エネルギーがそれぞれ \(E_i-\hbar\omega\) と \(E_f\) の始状態と終状態間の時間に依存しない摂動 \(U(x,y,z)\) と同じ効果を持っている」ことを示している.よく知られているように, [3] 例えば, D.L.Landau and E.M. Lifshitz,”Quantum Mechanics; Non-Relativistic Theory,” Addison-Wesley, Reading, Massachusetts, 1958, Sec. 40. を見よ. 最も重要な寄与は \(E_f=E_i-\hbar\omega\) となるような状態からである.
前の結果式 (2.7) を利用すると, 1秒あたりの遷移の確率は次である:
\begin{equation}
P_{fi}\,d\Omega = \frac{2\pi}{\hbar}\bigl|U_{fi}\bigr|^{2}\frac{\omega^{2}d\Omega}{(2\pi c)^{3}\hbar}
\tag{3.10}
\end{equation}
P_{fi}\,d\Omega = \frac{2\pi}{\hbar}\bigl|U_{fi}\bigr|^{2}\frac{\omega^{2}d\Omega}{(2\pi c)^{3}\hbar}
\tag{3.10}
\end{equation}
\(U_{fi}\) を決定するために次のように書く:
\begin{align}
H&=\frac{1}{2m}\left(\mb{p}-\frac{e}{c}\mb{A}\right)^{2}-\frac{e\hbar}{2mc}\mb{\sigma}\cdot\nabla\times\mb{A}
+eV\notag\\
&=\frac{1}{2m}\mb{p}\cdot\mb{p}+eV-\frac{e}{2mc}\bigl(\mb{p}\cdot\mb{A}+\mb{A}\cdot\mb{p}\bigr)-\frac{e\hbar}{2mc}
\mb{\sigma}\cdot\nabla\times\mb{A}+\frac{e^{2}}{2mc^{2}}\mb{A}\cdot\mb{A}
\tag{3.11}
\end{align}
H&=\frac{1}{2m}\left(\mb{p}-\frac{e}{c}\mb{A}\right)^{2}-\frac{e\hbar}{2mc}\mb{\sigma}\cdot\nabla\times\mb{A}
+eV\notag\\
&=\frac{1}{2m}\mb{p}\cdot\mb{p}+eV-\frac{e}{2mc}\bigl(\mb{p}\cdot\mb{A}+\mb{A}\cdot\mb{p}\bigr)-\frac{e\hbar}{2mc}
\mb{\sigma}\cdot\nabla\times\mb{A}+\frac{e^{2}}{2mc^{2}}\mb{A}\cdot\mb{A}
\tag{3.11}
\end{align}
ポテンシャルが作用するのは一度だけという規則 (これは1次の項だけを加えるのと同じである) の理由で, この問題に \(\mb{A}\cdot\mb{A}\) を含んだ項は加えない.\(\mb{A}=a\mb{e}\exp\{-i(\omega t-\mb{K}\cdot\mb{x})\}\) と次の2つの演算子の関係式を利用する:
-
\begin{align}
\nabla\times\mb{A}&=\nabla\times\bigl\{a\mb{e}\exp(-i\omega t)\exp(i\mb{K}\cdot\mb{x})\bigr\}
=-ae^{-i\omega t}\mb{e}\times\nabla e^{i\mb{K}\cdot\mb{x}}
=i\mb{K}\times\mb{e}ae^{-i\omega t}e^{i\mb{K}\cdot\mb{x}}\notag\\
&=iae^{-i\omega t}(\mb{K}\times\mb{e})\,e^{+i\mb{K}\cdot\mb{x}}
\tag{3.12}
\end{align} -
\begin{align*}
\mb{p}\,e^{+i\mb{K}\cdot\mb{x}}&=\bigl(\mb{p}e^{i\mb{K}\cdot\mb{x}}\bigr)+e^{i\mb{K}\cdot\mb{x}}\mb{p}
=-i\hbar\nabla e^{i\mb{K}\cdot\mb{x}}+e^{i\mb{K}\cdot\mb{x}}\mb{p}
=\hbar\mb{K}e^{i\mb{K}\cdot\mb{x}}+e^{i\mb{K}\cdot\mb{x}}\mb{p}\\
&=e^{+i\mb{K}\cdot\mb{x}}\bigl(\mb{p}+\hbar\mb{K}\bigr)
\end{align*}
または,
\begin{equation}
\mb{p}\cdot\mb{A}=ae^{-i\omega t}\mb{p}\cdot\mb{e}\,e^{+i\mb{K}\cdot\mb{x}}
=ae^{-i\omega t}e^{+i\mb{K}\cdot\mb{x}}\,\bigl(\mb{p}\cdot\mb{e}+\hbar\mb{K}\cdot\mb{e}\bigr)
=ae^{-i\omega t}\mb{p}\cdot\mb{e}\,e^{+i\mb{K}\cdot\mb{x}}
\tag{3.13}
\end{equation}
ただし \(\mb{K}\cdot\mb{e}=0\) である.これは Maxwell 方程式とゲージ選択 (すなわちゲージ条件として \(\nabla\times\mb{A}=0\) という「Coulombゲージ」を採用すること) から導かれる.すると, 次式のように書くことが出来る:
\begin{align}
U(x,y,z)&=-\frac{e}{2mc}\bigl(\mb{p}\cdot\mb{A}+\mb{A}\cdot\mb{p}\bigr)-\frac{e\hbar}{2mc}
\mb{\sigma}\cdot\nabla\times\mb{A}\notag\\
&=-\frac{e}{2mc}\Bigl\{ae^{-i\omega t}\mb{p}\cdot\mb{e}\,e^{+i\mb{K}\cdot\mb{x}}
+ae^{-i\omega t}\mb{e}\cdot\mb{p}\,e^{+i\mb{K}\cdot\mb{x}}\Bigr\}
-\frac{e\hbar}{2mc}\mb{\sigma}\cdot\bigl\{iae^{-i\omega t}(\mb{K}\times\mb{e})\,e^{+i\mb{K}\cdot\mb{x}}\bigr\}\notag\\
&=ae^{-i\omega t}\left[-\frac{e}{2mc}\Bigl\{\mb{p}\cdot\mb{e}\,e^{+i\mb{K}\cdot\mb{x}}
+\mb{e}\cdot\mb{p}\,e^{+i\mb{K}\cdot\mb{x}}\Bigr\}
-i\frac{e\hbar}{2mc}\mb{\sigma}\cdot(\mb{K}\times\mb{e})\,e^{+i\mb{K}\cdot\mb{x}}\right],\notag\\
\Delta H &=e^{i\omega t}U(x,y,z)=a\left[-\frac{e}{2mc}\Bigl\{\mb{p}\cdot\mb{e}\,e^{+i\mb{K}\cdot\mb{x}}
+\mb{e}\cdot\mb{p}\,e^{+i\mb{K}\cdot\mb{x}}\Bigr\}
-i\frac{e\hbar}{2mc}\mb{\sigma}\cdot(\mb{K}\times\mb{e})\,e^{+i\mb{K}\cdot\mb{x}}\right],\notag\\
U_{fi}&=\int \phi_{f}^{*}\Delta H\,\phi_i\,dVol\notag\\
&=a\int \phi_f^{*}\left[-\frac{e}{2mc}\bigl(\mb{p}\cdot\mb{e}\,e^{+i\mb{K}\cdot\mb{x}}
+e^{+i\mb{K}\cdot\mb{x}}\,\mb{e}\cdot\mb{p}\bigr)-i\frac{e\hbar}{2mc}\mb{\sigma}\cdot(\mb{K}\times\mb{e})
\,e^{+i\mb{K}\cdot\mb{x}}\right]\,\phi_i\,dVol\tag{3.14}\\
&=-a\int \phi_f^{*}\left[2\frac{e}{2mc}\mb{p}\cdot\mb{e}\,e^{+i\mb{K}\cdot\mb{x}}
+i\frac{e\hbar}{2mc}\mb{\sigma}\cdot(\mb{K}\times\mb{e})\,e^{+i\mb{K}\cdot\mb{x}}\right]\,\phi_i\,dVol
\end{align}
U(x,y,z)&=-\frac{e}{2mc}\bigl(\mb{p}\cdot\mb{A}+\mb{A}\cdot\mb{p}\bigr)-\frac{e\hbar}{2mc}
\mb{\sigma}\cdot\nabla\times\mb{A}\notag\\
&=-\frac{e}{2mc}\Bigl\{ae^{-i\omega t}\mb{p}\cdot\mb{e}\,e^{+i\mb{K}\cdot\mb{x}}
+ae^{-i\omega t}\mb{e}\cdot\mb{p}\,e^{+i\mb{K}\cdot\mb{x}}\Bigr\}
-\frac{e\hbar}{2mc}\mb{\sigma}\cdot\bigl\{iae^{-i\omega t}(\mb{K}\times\mb{e})\,e^{+i\mb{K}\cdot\mb{x}}\bigr\}\notag\\
&=ae^{-i\omega t}\left[-\frac{e}{2mc}\Bigl\{\mb{p}\cdot\mb{e}\,e^{+i\mb{K}\cdot\mb{x}}
+\mb{e}\cdot\mb{p}\,e^{+i\mb{K}\cdot\mb{x}}\Bigr\}
-i\frac{e\hbar}{2mc}\mb{\sigma}\cdot(\mb{K}\times\mb{e})\,e^{+i\mb{K}\cdot\mb{x}}\right],\notag\\
\Delta H &=e^{i\omega t}U(x,y,z)=a\left[-\frac{e}{2mc}\Bigl\{\mb{p}\cdot\mb{e}\,e^{+i\mb{K}\cdot\mb{x}}
+\mb{e}\cdot\mb{p}\,e^{+i\mb{K}\cdot\mb{x}}\Bigr\}
-i\frac{e\hbar}{2mc}\mb{\sigma}\cdot(\mb{K}\times\mb{e})\,e^{+i\mb{K}\cdot\mb{x}}\right],\notag\\
U_{fi}&=\int \phi_{f}^{*}\Delta H\,\phi_i\,dVol\notag\\
&=a\int \phi_f^{*}\left[-\frac{e}{2mc}\bigl(\mb{p}\cdot\mb{e}\,e^{+i\mb{K}\cdot\mb{x}}
+e^{+i\mb{K}\cdot\mb{x}}\,\mb{e}\cdot\mb{p}\bigr)-i\frac{e\hbar}{2mc}\mb{\sigma}\cdot(\mb{K}\times\mb{e})
\,e^{+i\mb{K}\cdot\mb{x}}\right]\,\phi_i\,dVol\tag{3.14}\\
&=-a\int \phi_f^{*}\left[2\frac{e}{2mc}\mb{p}\cdot\mb{e}\,e^{+i\mb{K}\cdot\mb{x}}
+i\frac{e\hbar}{2mc}\mb{\sigma}\cdot(\mb{K}\times\mb{e})\,e^{+i\mb{K}\cdot\mb{x}}\right]\,\phi_i\,dVol
\end{align}
この結果は厳密なものである.これは, いわゆる「電気双極子近似」を用いることで簡単化できる.この近似を導くために, 項
\(\displaystyle \frac{e}{2mc}\,\mb{p}\cdot\mb{e}\,e^{+i\mb{K}\cdot\mb{x}}\) を考える.これは原子中の電子速度または電流の次元・大きさである.指数は展開することが可能である:
\begin{equation}
e^{+i\mb{K}\cdot\mb{x}}=1+i\mb{K}\cdot\mb{x}+\frac{1}{2}\bigl(i\mb{K}\cdot\mb{x}\bigr)^{2}+\dotsb
\tag{3.15}
\end{equation}
e^{+i\mb{K}\cdot\mb{x}}=1+i\mb{K}\cdot\mb{x}+\frac{1}{2}\bigl(i\mb{K}\cdot\mb{x}\bigr)^{2}+\dotsb
\tag{3.15}
\end{equation}
\(\displaystyle\mb{K}\cdot\mb{x}\approx\frac{2\pi}{\lambda}x\) は \(a_0/\lambda\) のオーダーである.ただし \(a_0\) は原子の大きさ, そして \(\lambda\) は波長である.もし \(a_0/\lambda\ll 1\) であるならば \(a_0/\lambda\) について一次よりも高次の項は全て無視することが出来る.双極子近似を完成するためには, 最後の項を無視することも必要である.これをする訳は簡単である.というのは, 最後の項は \(\displaystyle \frac{\hbar K}{mc}=\frac{\hbar K c}{mc^{2}}=\frac{mv^{2}}{mc^{2}}\) のオーダーと見做せるからである.このような項は無視できるが, これは過大評価である.より正確には次である:
\begin{equation}
\frac{ie\hbar}{2mc}\mb{\sigma}\cdot\bigl(\mb{K}\times\mb{e}\bigr)\,e^{+i\mb{K}\cdot\mb{x}}
\approx \frac{v}{c}\times[\,\mathrm{matrix\ element\ of}\ \mb{\sigma}\cdot\bigl(\mb{K}\times\mb{p}\bigr)\,]
\tag{3.16}
\end{equation}
\frac{ie\hbar}{2mc}\mb{\sigma}\cdot\bigl(\mb{K}\times\mb{e}\bigr)\,e^{+i\mb{K}\cdot\mb{x}}
\approx \frac{v}{c}\times[\,\mathrm{matrix\ element\ of}\ \mb{\sigma}\cdot\bigl(\mb{K}\times\mb{p}\bigr)\,]
\tag{3.16}
\end{equation}
行列要素は次である:
\begin{equation}
\int \phi_f^{*}\,\mb{\sigma}\cdot\bigl(\mb{K}\times\mb{p}\bigr)\,\phi_i\,dVol
\tag{3.17}
\end{equation}
\int \phi_f^{*}\,\mb{\sigma}\cdot\bigl(\mb{K}\times\mb{p}\bigr)\,\phi_i\,dVol
\tag{3.17}
\end{equation}
よい近似値として, 次のような分離をすることが出来る:
\begin{equation}
\phi_f^{*}=\phi_f^{*}(\mb{x})\,U_f^{*}(\mathrm{spin}),\quad\text{and}\quad
\phi_i = \phi_i(\mb{x})\,U_i(\mathrm{spin})
\tag{3.18}
\end{equation}
\phi_f^{*}=\phi_f^{*}(\mb{x})\,U_f^{*}(\mathrm{spin}),\quad\text{and}\quad
\phi_i = \phi_i(\mb{x})\,U_i(\mathrm{spin})
\tag{3.18}
\end{equation}
するとこの近似の正確さに於いて, 積分は
\begin{equation}
\int \phi_f^{*}(\mb{x})\phi_i(\mb{x})\,U_f^{*}\,\mb{\sigma}\cdot\bigl(\mb{K}\times\mb{p}\bigr)\,U_i\,dVol =0
\tag{3.19}
\end{equation}
\int \phi_f^{*}(\mb{x})\phi_i(\mb{x})\,U_f^{*}\,\mb{\sigma}\cdot\bigl(\mb{K}\times\mb{p}\bigr)\,U_i\,dVol =0
\tag{3.19}
\end{equation}
なぜなら,状態は直交しているからである. [4][ 訳註 ] この式 (3.16)\(\sim\)式 (3.19) は理解できなかった.\(\mb{\sigma}\cdot(\mb{K}\times\mb{p})\) は \(\mb{\sigma}\cdot(\mb{K}\times\mb{e})\) … Continue reading
差し当たり(For the present), 双極子近似が用いられている.すると \(e^{i\mb{K}\cdot\mb{x}}\simeq 1\) と近似して,
\begin{equation*}
U_{fi}=-a\int \phi_f^{*}\left(2\frac{e}{2mc}\mb{p}\cdot\mb{e}\,e^{i\mb{K}\cdot\mb{x}}\right)\phi_i\,dV
=-a\frac{e}{mc}\int \phi_f^{*}\mb{p}\cdot\mb{e}\phi_i\,dV
\end{equation*}
U_{fi}=-a\int \phi_f^{*}\left(2\frac{e}{2mc}\mb{p}\cdot\mb{e}\,e^{i\mb{K}\cdot\mb{x}}\right)\phi_i\,dV
=-a\frac{e}{mc}\int \phi_f^{*}\mb{p}\cdot\mb{e}\phi_i\,dV
\end{equation*}
従って,
\begin{equation}
U_{fi}=-a\,\frac{\,e\,}{mc}\,\mb{p}_{fi}\cdot\mb{e},\quad
\text{where}\quad \mb{p}_{fi}\cdot\mb{e}=\int \phi_f^{*}\,\bigl(\mb{p}\cdot\mb{e}\bigr)\,\phi_i
=\mb{e}\cdot\int \phi_f^{*}\,\mb{p}\,\phi_i\,dVol
\tag{3.20}
\end{equation}
U_{fi}=-a\,\frac{\,e\,}{mc}\,\mb{p}_{fi}\cdot\mb{e},\quad
\text{where}\quad \mb{p}_{fi}\cdot\mb{e}=\int \phi_f^{*}\,\bigl(\mb{p}\cdot\mb{e}\bigr)\,\phi_i
=\mb{e}\cdot\int \phi_f^{*}\,\mb{p}\,\phi_i\,dVol
\tag{3.20}
\end{equation}
従って, 式 (3.10) から
\begin{equation}
P_{fi}\,d\Omega = \frac{2\pi}{\hbar}\bigl|U_{fi}\bigr|^{2}\frac{\omega^{2}}{(2\pi c)^{3}\hbar}d\Omega
=\frac{2\pi}{\hbar}\left(\frac{e}{mc}a\right)^{2}\bigl|\mb{p}_{fi}\cdot\mb{e}\bigr|^{2}\,d\Omega\,
\frac{\omega^{2}}{(2\pi c)^{3}\hbar}
\tag{3.21}
\end{equation}
P_{fi}\,d\Omega = \frac{2\pi}{\hbar}\bigl|U_{fi}\bigr|^{2}\frac{\omega^{2}}{(2\pi c)^{3}\hbar}d\Omega
=\frac{2\pi}{\hbar}\left(\frac{e}{mc}a\right)^{2}\bigl|\mb{p}_{fi}\cdot\mb{e}\bigr|^{2}\,d\Omega\,
\frac{\omega^{2}}{(2\pi c)^{3}\hbar}
\tag{3.21}
\end{equation}
演算子の代数を用いると \(\displaystyle \frac{\mb{p}_{fi}}{m}=i\omega\mb{x}_{fi}\) である.[5][ 訳註 ] 原文では \(\displaystyle \frac{\mb{p}_{fi}}{m}=\hbar\omega_{fi}\mb{x}_{fi}\) となっているが, 次の理由から修正した.位置演算子 \(\mb{x}\) … Continue reading
従って,
\begin{equation}
P_{fi}\,d\Omega =\frac{2\pi}{\hbar}\left(\frac{ea}{c}\right)^{2}\left|i\omega\mb{x}_{fi}\cdot\mb{e}\right|^{2}
\frac{\omega^{2}}{(2\pi c)^{3}\hbar}\,d\Omega
= \frac{a^{2}}{\hbar^{2}c^{5}}\frac{e^{2}\omega^{4}}{(2\pi)^{2}}\,\bigl(\mb{e}\cdot\mb{x}_{fi}\bigr)^{2}\,d\Omega
\tag{3.22}
\end{equation}
P_{fi}\,d\Omega =\frac{2\pi}{\hbar}\left(\frac{ea}{c}\right)^{2}\left|i\omega\mb{x}_{fi}\cdot\mb{e}\right|^{2}
\frac{\omega^{2}}{(2\pi c)^{3}\hbar}\,d\Omega
= \frac{a^{2}}{\hbar^{2}c^{5}}\frac{e^{2}\omega^{4}}{(2\pi)^{2}}\,\bigl(\mb{e}\cdot\mb{x}_{fi}\bigr)^{2}\,d\Omega
\tag{3.22}
\end{equation}
ただし \(\displaystyle \mb{x}_{fi}=\int \phi_f^{*}\mb{x}\phi_i\,dV\) である.全確率は \(P_{fi}\)を\(d\Omega\) について積分することで得られる.よって,
\begin{align}
\mathrm{Total prob./sec}&=\int \frac{a^{2}}{\hbar^{2} c^{5}}\,\frac{e^{2}\omega^{4}}{(2\pi)^{2}}\bigl(\mb{e}\cdot\mb{x}_{fi}\bigr)^{2}\,d\Omega
=\frac{a^{2}}{\hbar^{2} c^{5}}\,\frac{e^{2}\omega^{4}}{(2\pi)^{2}}\int_{0}^{2\pi}d\phi\int_0^{\pi}\sin^{2}\theta\,d\theta\,\bigl(\mb{e}\cdot\mb{x}_{fi}\bigr)^{2}\notag\\
&=\frac{a^{2}}{\hbar^{2} c^{5}}\,\frac{e^{2}\omega^{4}}{(2\pi)^{2}}2\pi\int_0^{\pi}\sin\theta\,d\theta\,|\mb{x}_{fi}|^{2}\sin^{2}\theta
=\frac{a^{2}}{\hbar^{2} c^{5}}\frac{e^{2}\omega^{4}}{2\pi}|\mb{x}_{fi}|^{2}\int_{0}^{\pi}\sin^{3}\theta\,d\theta\notag\\
&=\frac{a^{2}}{\hbar^{2} c^{5}}\frac{e^{2}\omega^{4}}{2\pi}|\mb{x}_{fi}|^{2}\cdot\frac{4}{3}
=\frac{a^{2}}{\hbar^{2} c^{5}}4e^{2}\omega^{4}\frac{|\mb{x}_{fi}|^{2}}{6\pi}
\tag{3.23}
\end{align}
\mathrm{Total prob./sec}&=\int \frac{a^{2}}{\hbar^{2} c^{5}}\,\frac{e^{2}\omega^{4}}{(2\pi)^{2}}\bigl(\mb{e}\cdot\mb{x}_{fi}\bigr)^{2}\,d\Omega
=\frac{a^{2}}{\hbar^{2} c^{5}}\,\frac{e^{2}\omega^{4}}{(2\pi)^{2}}\int_{0}^{2\pi}d\phi\int_0^{\pi}\sin^{2}\theta\,d\theta\,\bigl(\mb{e}\cdot\mb{x}_{fi}\bigr)^{2}\notag\\
&=\frac{a^{2}}{\hbar^{2} c^{5}}\,\frac{e^{2}\omega^{4}}{(2\pi)^{2}}2\pi\int_0^{\pi}\sin\theta\,d\theta\,|\mb{x}_{fi}|^{2}\sin^{2}\theta
=\frac{a^{2}}{\hbar^{2} c^{5}}\frac{e^{2}\omega^{4}}{2\pi}|\mb{x}_{fi}|^{2}\int_{0}^{\pi}\sin^{3}\theta\,d\theta\notag\\
&=\frac{a^{2}}{\hbar^{2} c^{5}}\frac{e^{2}\omega^{4}}{2\pi}|\mb{x}_{fi}|^{2}\cdot\frac{4}{3}
=\frac{a^{2}}{\hbar^{2} c^{5}}4e^{2}\omega^{4}\frac{|\mb{x}_{fi}|^{2}}{6\pi}
\tag{3.23}
\end{align}
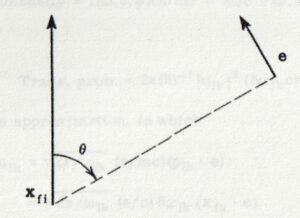
ただし, 項 \(\mb{e}\cdot\mb{x}_{fi}\) は次式に注意することで決定されることを用いている (図 3-1 を参照) :
\begin{equation}
|\mb{x}_{fi}\cdot\mb{e}|=|\mb{x}_{fi}|\cdot|\mb{e}|\cos\left(\frac{\pi}{2}-\theta\right)=|\mb{x}_{fi}|\sin\theta
\tag{3.24}
\end{equation}
|\mb{x}_{fi}\cdot\mb{e}|=|\mb{x}_{fi}|\cdot|\mb{e}|\cos\left(\frac{\pi}{2}-\theta\right)=|\mb{x}_{fi}|\sin\theta
\tag{3.24}
\end{equation}
式 (2.6) から \(\displaystyle a=\sqrt{\frac{4\pi\hbar c^{2}}{2\omega}}=\sqrt{\frac{2\pi\hbar c^{2}}{\omega}}\) である.これを式 (3.23) に代入して次を得る:[6] [ 訳註 ] 式(3.25)の結果はランダウ:「量子力学」§97の式(97.4)に一致している.
\begin{align}
\mathrm{Total prob./sec}&=\frac{a^{2}}{\hbar^{2} c^{5}}4e^{2}\omega^{4}\frac{|\mb{x}_{fi}|^{2}}{6\pi}
=\frac{1}{\hbar^{2}c^{5}}\cdot\frac{2\pi\hbar c^{2}}{\omega}\cdot\frac{4e^{2}\omega^{4}}{6\pi}|\mb{x}_{fi}|^{2}\notag\\
&=\frac{4}{3}\cdot\frac{e^{2}}{\hbar c}\frac{\omega^{3}}{c^{2}}|\mb{x}_{fi}|^{2}
=\frac{4}{3}\alpha \frac{\omega^{3}}{c^{2}}|\mb{x}_{fi}|^{2}\notag\\
&=\frac{4\omega^{3}}{3\hbar c^{3}}|\mb{d}_{fi}|^{2}
\tag{3.25}
\end{align}
\mathrm{Total prob./sec}&=\frac{a^{2}}{\hbar^{2} c^{5}}4e^{2}\omega^{4}\frac{|\mb{x}_{fi}|^{2}}{6\pi}
=\frac{1}{\hbar^{2}c^{5}}\cdot\frac{2\pi\hbar c^{2}}{\omega}\cdot\frac{4e^{2}\omega^{4}}{6\pi}|\mb{x}_{fi}|^{2}\notag\\
&=\frac{4}{3}\cdot\frac{e^{2}}{\hbar c}\frac{\omega^{3}}{c^{2}}|\mb{x}_{fi}|^{2}
=\frac{4}{3}\alpha \frac{\omega^{3}}{c^{2}}|\mb{x}_{fi}|^{2}\notag\\
&=\frac{4\omega^{3}}{3\hbar c^{3}}|\mb{d}_{fi}|^{2}
\tag{3.25}
\end{align}
ただし \(\displaystyle \alpha=\frac{e^{2}}{\hbar c}=\frac{1}{137.04}\) は「微細構造定数」である.そして \(\mb{d}=e\mb{x}\) は, 電子の (軌道運動の)「双極子モーメント」である.
References
| ↑1 | [ 訳註 ] ファインマンはゲージ変換の式 (3.1)\(\sim\)(3.4) を次のように記している: if \(\mathbf{E}=-\nabla \phi +\partial\phi/\partial t\) and \(\mathbf{B}=\nabla\times\mathbf{A}\), and if \(\chi\) is any scalar, then the substitutions \(\mathbf{A}’=\mathbf{A}+\nabla\chi\), \(\phi’=\phi+\partial\chi/\partial t\) leave \(\mathbf{E}\) and \(\mathbf{B}\) invariant. しかし, これは明らかに単純な書き間違えであろう.また, 式 (3.5) は次のように変更した: \begin{equation*} \psi’=e^{-i\chi}\psi, \quad \rightarrow\quad \psi’=\exp\left(i\frac{e}{\hbar c}\chi\right)\,\psi \end{equation*} |
|---|---|
| ↑2 | [ 訳註 ] 【 参考 】 (A) \(\phi\) をスカラー量とするとき「\(\nabla\times\nabla\phi=0\)」となる.このベクトル解析の重要な公式が成り立つことは, その成分を具体的に計算すれば容易に分かることである.\(\chi\) をスカラー量であるとしてこの公式を利用すると,「\(\mb{E}\) と \(\mb{B}\) が不変に保たれること」は, 容易に確かめることが出来る: \begin{align*} \mb{E}’&=-\nabla\phi’-\ppdiff{\mb{A}’}{t} =-\nabla\left(\phi-\ppdiff{\chi}{t}\right)-\pdiff{t}\left(\mb{A}+\nabla\chi\right)\\ &=-\nabla\phi+\pdiff{t}\nabla\chi -\ppdiff{\mb{A}}{t}-\pdiff{t}\nabla\chi =-\nabla\phi-\ppdiff{\mb{A}}{t}=\mb{E},\\ \mb{B}’&=\nabla\times\mb{A}’=\nabla\times\left(\mb{A}+\nabla\chi\right) =\nabla\times\mb{A}+\underbrace{\nabla\times\nabla\chi}_{=0} =\nabla\times\mb{A}=\mb{B} \end{align*} (B) [Landau and Lifshitz : Quantum Electrodynamics §33] 非相対論的極限 (\(v\to0\))で, 双スピノール \(\psi\) の2つの成分(即ち\(\chi\)) がゼロになる(§21).従って, 電子の速度が小さいときは \(\phi\gg \chi\) である.これから形式的に波動関数を \(1/c\) について冪展開することにより, 2成分量 \(\phi\) だけを含む近似方程式を得る可能性が与えられる. 外場内の電子に対するディラック方程式から出発しよう: \begin{equation*} i\hbar \ppdiff{\psi}{t}=\left\{c\mb{\alpha}\left(\hat{\mb{p}}-\frac{e}{c}\mb{A}\right) +\beta mc^{2}+e\Phi\right\}\psi \tag{33.1} \end{equation*} 粒子の相対論的エネルギーには, その静止エネルギーも含まれる.非相対論的近似へ移るときに, それは消去されなければならない.従って次式のように定義される関数 \(\psi’\) で \(\psi\) を置き換える: \begin{equation*} \psi =\psi’ e^{-imc^{2}t/\hbar} \end{equation*} すると, \begin{equation*} \left(i\hbar\pdiff{t}+mc^{2}\right)\psi’ = \left\{c\mb{\alpha}\cdot\left(\hat{\mb{p}}-\frac{e}{c}\mb{A} \right)+\beta mc^{2}+e\Phi\right\}\psi’ \end{equation*} \(\psi’=\begin{pmatrix} \phi’ \\ \chi’ \end{pmatrix}\) を代入すると次式を得る: \begin{align*} \left(i\hbar \pdiff{t}-e\Phi\right)\phi’ &= c\mb{\sigma}\cdot\left(\hat{\mb{p}}-\frac{e}{c}\mb{A}\right) \chi’\tag{33.2}\\ \left(i\hbar \pdiff{t}-e\Phi+2mc^{2}\right)\chi’ &= c\mb{\sigma}\cdot\left(\hat{\mb{p}}-\frac{e}{c}\mb{A}\right) \phi’\tag{33.3} \end{align*} 以下では \(\phi\) と \(\chi\) のプライム符号(\(‘\))を省略する;こうしても誤解は起こさないであろう.なぜならこの節では変換した関数 \(\psi’\) だけを使うからである. 1次近似では式 (33.3) の左辺で \(2mc^{2}\chi\) だけを残こす(retain 保持する).すると次を得る: \begin{equation*} 2mc^{2}\chi=c\mb{\sigma}\cdot\left(\hat{\mb{p}}-\frac{e}{c}\mb{A}\right)\phi\quad\rightarrow\quad \chi =\frac{1}{2mc}\mb{\sigma}\cdot\left(\hat{\mb{p}}-\frac{e}{c}\mb{A}\right)\phi \tag{33.4} \end{equation*} (従って \(\chi\sim \phi/c\) である).これを式 (33.2) に代入すると次となる: \begin{equation*} \left(i\hbar \pdiff{t}-e\Phi\right)\phi=\frac{1}{2m} \left\{\mb{\sigma}\cdot \left(\hat{\mb{p}}-\frac{e}{c}\mb{A}\right)\right\}^{2}\phi \end{equation*} パウリ行列に対して次の関係式が成り立つ: \begin{equation*} \left(\mb{\sigma}\cdot\mb{a}\right)\left(\mb{\sigma}\cdot\mb{b}\right) =\mb{a}\cdot\mb{b}+i\mb{\sigma}\cdot\mb{a}\times\mb{b} \tag{33.5} \end{equation*} ただし \(\mb{a}\) と \(\mb{b}\) は任意のベクトルである (この式はパウリ行列の基本的性質 \([\sigma_i,\sigma_k]=2\delta_{ik}\), \(\sigma_i\sigma_k=i\varepsilon_{ikl}\sigma_l +\delta_{ik}\) から導出することが出来る).今の場合 \(\displaystyle \mb{a}=\mb{b}=\hat{\mb{p}}-\frac{e}{c}\mb{A}\) である.しかしベクトル積 \(\mb{a}\times\mb{b}\) はゼロではない.なぜなら \(\hat{\mb{p}}\) と \(\mb{A}\) は交換しないからである: \begin{align*} \left[\left(\hat{\mb{p}}-\frac{e}{c}\mb{A}\right)\times\left(\hat{\mb{p}}-\frac{e}{c}\mb{A}\right) \right]\phi &=i\frac{e\hbar}{c}\big\{\mb{A}\times\nabla+\nabla\times\mb{A}\big\}\phi\\ &=i\frac{e\hbar}{c}\,\mathrm{curl}\,\mb{A}\cdot \phi \end{align*} 従って, \begin{equation*} \left\{\mb{\sigma}\cdot \left(\hat{\mb{p}}-\frac{e}{c}\mb{A}\right)\right\}^{2} =\left(\hat{\mb{p}}-\frac{e}{c}\mb{A}\right)^{2}-\frac{e\hbar}{c}\mb{\sigma}\cdot\mb{H} \tag{33.6} \end{equation*} ただし \(\mb{H}=\mathrm{curl}\,\mb{A}\) は磁場である.書き換え \(\Phi\to\phi,\phi\to\psi\) としたとき, \(\psi\) に対して次の方程式が得られる: \begin{equation*} i\hbar\ppdiff{\psi}{t}=\hat{\mb{H}}\psi=\left[\frac{1}{2m}\left(\hat{\mb{p}} -\frac{e}{c}\mb{A}\right)^{2}+e\phi-\frac{e\hbar}{2mc}\mb{\sigma}\cdot\mb{H}\right]\psi \tag{33.7} \end{equation*} これがいわゆる「パウリ方程式」である.これはハミルトニアンに最後の項が現れる点で, 非相対論的シュレディンガー方程式と異なっている.この項は外場内に於ける磁気的2重極のポテンシャルエネルギーの形をしている.このようにして \((1/c)\) に関する一次近似では, 電子は電荷と共に磁気モーメント \begin{equation*} \mb{\mu}=\frac{e\hbar}{2mc}\mb{\sigma}=\frac{e}{mc}\hbar\mb{s} \tag{33.8} \end{equation*} を持つ粒子のように振る舞う.この磁気回転比 \((e/mc)\) は軌道運動の磁気モーメントに対するものの2倍の大きさである.この注目すべき結果は 1928 年にディラックにより得られた.方程式 (33.7) の満足する2成分波動関数はパウリにより 1927 年に導かれた.これはディラックによるその方程式の発見以前のことである. (C) 前述で, 式 (3.1) はパウリ方程式 (33.7) に等価であることが示されたので, この式 (33.7) に対してゲージ変換 (3.2) を施してみよう: \begin{equation*} i\hbar\ppdiff{\psi’}{t}=\left[\frac{1}{2m}\left(\hat{\mb{p}} -\frac{e}{c}\mb{A}’\right)^{2}+e\phi’-\frac{e\hbar}{2mc}\mb{\sigma}\cdot\mb{H}\right]\psi’ \tag{1} \end{equation*} この左辺は, \begin{align*} i\hbar\pdiff{t}\psi’&=i\hbar \pdiff{t}\exp\left(i\frac{e}{\hbar c}\chi\right)\psi =i\hbar\times\left(i\frac{e}{\hbar c}\ppdiff{\chi}{t}\right)\exp\left(i\frac{e}{\hbar c}\chi\right)\psi +\exp\left(i\frac{e}{\hbar c}\chi\right)\left(i\hbar\ppdiff{\psi}{t}\right)\\ &=\exp\left(i\frac{e}{\hbar c}\chi\right)\left(i\hbar\ppdiff{\psi}{t}-\frac{e}{c}\ppdiff{\chi}{t}\psi\right) \tag{2} \end{align*} 右辺は, \begin{align*} &\left[\frac{1}{2m}\left(\hat{\mb{p}} -\frac{e}{c}\mb{A}’\right)^{2}+e\phi’-\frac{e\hbar}{2mc}\mb{\sigma}\cdot\mb{H}\right]\psi’\\ &\quad =\frac{1}{2m}\left\{\hat{\mb{p}}-\frac{e}{c}\left(\mb{A}+\nabla\chi\right)\right\}^{2}\psi’ +e\left(\phi-\frac{1}{c}\ppdiff{\chi}{t}\right)\psi’ -\frac{e\hbar}{2mc}\mb{\sigma}\cdot\mb{H}\psi’\\ &\quad =\exp\left(i\frac{e}{\hbar c}\chi\right)\frac{1}{2m}\left(\mb{p}-\frac{e}{c}\mb{A}\right)^{2}\psi +\exp\left(i\frac{e}{\hbar c}\chi\right)\left(e\,\phi -\frac{e}{c}\ppdiff{\chi}{t}\right)\psi -\exp\left(i\frac{e}{\hbar c}\chi\right)\frac{e\hbar}{2mc}\mb{\sigma}\cdot\mb{H}\psi\\ &\quad =\exp\left(i\frac{e}{\hbar c}\chi\right)\left[\frac{1}{2m}\left(\mb{p}-\frac{e}{c}\mb{A}\right)^{2} +e\,\phi -\frac{e}{c}\ppdiff{\chi}{t}-\frac{e\hbar}{2mc}\mb{\sigma}\cdot\mb{H}\right]\psi \tag{3} \end{align*} 式 (2) と式 (3) から, 式 (1) はゲージ変換前の式 (33.7) の形に一致することが示される: \begin{align*} &\exp\left(i\frac{e}{\hbar c}\chi\right)\left(i\hbar\ppdiff{\psi}{t}-\frac{e}{c}\ppdiff{\chi}{t}\right) =\exp\left(i\frac{e}{\hbar c}\chi\right)\left[\frac{1}{2m}\left(\mb{p}-\frac{e}{c}\mb{A}\right)^{2} +e\,\phi -\frac{e}{c}\ppdiff{\chi}{t}-\frac{e\hbar}{2mc}\mb{\sigma}\cdot\mb{H}\right]\psi\\ &\rightarrow\quad i\hbar\ppdiff{\psi}{t}-\frac{e}{c}\ppdiff{\chi}{t} =\frac{1}{2m}\left[\left(\mb{p}-\frac{e}{c}\mb{A}\right)^{2} +e\,\phi -\frac{e}{c}\ppdiff{\chi}{t}-\frac{e\hbar}{2mc}\mb{\sigma}\cdot\mb{H}\right]\psi\\ &\therefore\quad i\hbar\ppdiff{\psi}{t}=\frac{1}{2m}\left[\left(\mb{p}-\frac{e}{c}\mb{A}\right)^{2} +e\,\phi -\frac{e\hbar}{2mc}\mb{\sigma}\cdot\mb{H}\right]\psi \end{align*} |
| ↑3 | 例えば, D.L.Landau and E.M. Lifshitz,”Quantum Mechanics; Non-Relativistic Theory,” Addison-Wesley, Reading, Massachusetts, 1958, Sec. 40. を見よ. |
| ↑4 | [ 訳註 ] この式 (3.16)\(\sim\)式 (3.19) は理解できなかった.\(\mb{\sigma}\cdot(\mb{K}\times\mb{p})\) は \(\mb{\sigma}\cdot(\mb{K}\times\mb{e})\) の誤植ではなかろうか?.そして, 式は次のように書けるので \(\mb{p}\approx\hbar/r_{\mathrm{atom}}\) と \(\hbar\mb{K}\approx \hbar2\pi/\lambda_{\mathrm{photon}}\) との比較になるのではないか?: \begin{equation*} \frac{e\hbar}{2mc}\mb{\sigma}\cdot(\mb{K}\times\mb{e})e^{i\mb{K}\cdot\mb{x}} =\frac{e}{2mc}\mb{\sigma}\cdot(\hbar\mb{K}\times\mb{e})e^{i\mb{K}\cdot\mb{x}} \end{equation*} ランダウ:「量子力学」§97に次の文章がある:「因子 \(e^{-i\mb{k}\cdot\mb{x}}\) が系の差し渡しの範囲 \(a\), 即ち関数 \(\phi_i\) と \(\phi_f\) が著しくゼロと異なる領域では僅かしか変わらないのでこれを \(1\) で置き換えることが出来る.このような置き換えは言い換えれば, 系の中で粒子の運動量に比べて光子の運動量を無視することである (普通の単位で, 後者は \(\hbar\mb{k}\) で, 前者は \(\hbar/a\) である)」.また J.J.Sakurai の §2.4 には次の文章がある:「スピン磁気能率による相互作用も無視できる.これを理解するには \(\mb{p}\approx \hbar/r_{\mathrm{atom}}\) のオーダーであり \(\hbar\mb{K}\approx \hbar (2\pi/\lambda_{\mathrm{photon}})\) なので \(\mb{p}/\hbar\mb{K}\approx (\lambda_{\mathrm{photon}}/2\pi)/r_{\mathrm{atom}}\) となるから, \(\mb{p}\) の行列要素 \(\displaystyle\frac{e}{mc}\mb{e}\cdot\mb{p}\) が \(\displaystyle\frac{e\hbar}{2mc}\mb{\sigma}\cdot(\mb{K}\times\mb{e})\) のそれよりも \((\lambda_{\mathrm{photon}}/2\pi)/r_{\mathrm{atom}}\) だけ大きいことだけに注意すればよい」. |
| ↑5 | [ 訳註 ] 原文では \(\displaystyle \frac{\mb{p}_{fi}}{m}=\hbar\omega_{fi}\mb{x}_{fi}\) となっているが, 次の理由から修正した.位置演算子 \(\mb{x}\) に対するハイゼンベルグの運動方程式より \begin{equation*} \frac{d\mb{x}}{dt}=\frac{1}{i\hbar}\bigl[\mb{x},H\bigr]\quad \rightarrow\quad \frac{\mb{p}}{m}=\frac{d\mb{x}}{dt}=\frac{-i}{\hbar}\bigl[\mb{x},H\bigr]=\frac{i}{\hbar}\bigl[H,\mb{x}\bigr] \end{equation*} 従って \(E_f-E_i=\hbar\omega\) とおくならば, \begin{align*} \frac{\mb{p}_{fi}}{m}&=\frac{i}{\hbar}\int \phi_f^{*}(H\mb{x}-\mb{x}H)\phi_i\,dV =\frac{i}{\hbar}\left\{\int (H\phi_f)^{*}\mb{x}\phi_i\,dV-\int\phi_f^{*}\mb{x}(H\phi_i)\,dV\right\}\\ &=\frac{i}{\hbar}\left\{E_f\int \phi_f^{*}\mb{x}\phi_i\,dV – E_i\int \phi_f^{*}\mb{x}\phi_i\,dV\right\} =\frac{i}{\hbar}(E_f-E_i)\int \phi_f^{*}\mb{x}\phi_i\,dV=i\omega\,\mb{x}_{fi} \end{align*} |
| ↑6 | [ 訳註 ] 式(3.25)の結果はランダウ:「量子力学」§97の式(97.4)に一致している. |