\(\)
ファインマンの第6講の最後には「自己エネルギー」の記述があるが, そこの式 (1.6.12) の導出などは書かれていない.より詳しい議論が J.J.Sakurai の§ 2-8 にあったので, それを書いておこう.
自己エネルギー問題(Self-energy problem)
考えるのは束縛電子または自由電子としよう.電子が存在することがまさに, その電子に付随する電磁場が存在することを意味している.古典的には, 電子の存在に依る電磁場はその電子自身に反応する可能性があり, H.ポアンケア や M.エイブラハム そして H.A.ローレンツによって詳しく議論された [1] Jackson (1962), pp. 578-597..放射の量子論では類似の効果があり, それは次の2段階のプロセスとして視覚化できる:
- 電子が(仮想)光子を放出する.
- その光子は同じ電子に吸収される.
電子自身の存在による電子と電磁場の(古典的または量子化された)相互作用エネルギーは, 電子の「自己エネルギー」と呼ばれる.現実的には電磁相互作用をオフにする方法がないため, 電子の自己エネルギーはその電子の観測可能な静止エネルギーとは切り離せない一部分になっている.この節では(観測不可能な)自己エネルギーを生み出す力学的メカニズムが, 原子状態の(観測可能な)エネルギー準位に重大な影響を及ぼすことを示そうと思う.
自己エネルギーの問題はいくつかのレベルで論じることが出来る.まず始めに, この問題は古典静電気学でも生じる.電荷分布 \(\rho\) を持つ電子モデルを考えることにする.電子が存在することで生じる静電ポテンシャルを \(\phi\) とする.すると相互作用エネルギーは次で与えられる:
\def\pdiff#1{\frac{\partial}{\partial #1}}
\def\reverse#1{\frac{1}{#1}}
\def\Bppdiff#1#2{\frac{\partial^{2} #1}{\partial #2^{2}}}
\def\ppdiff#1#2{\frac{\partial #1}{\partial #2}}
\def\BK#1#2{\langle #1 | #2 \rangle}
\def\BraKet#1#2#3{\langle #1 | #2 | #3 \rangle}
\def\ket#1{| #1 \rangle}
\def\bra#1{\langle #1 |}
\def\mb#1{\mathbf{#1}}
E_{\mathrm{int}}=\frac{1}{2}\int \rho\,\phi\,d^{3}x
\tag{2.222}
\end{equation}
もし電子が原点に位置する電荷 \(e\) の点粒子であれば \(\rho=e\,\delta(x)\) そして \(\phi=e/4\pi r\) となり, 従って \(E_{\mathrm{int}}\) は無限大となる.その代わりに, 一様な密度の球状の電荷分布を考えることが出来る.このようなモデルでは, 電子の静止エネルギーのかなりの部分を自己エネルギーに帰するのであれば, 電子の「半径」は古典的な電子半径 \(r_0=(e^2/4 \pi mc^2)\) のオーダーでなければならない.電子の自己エネルギーをディラックの相対論的電子理論を用いて量子力学的に計算すると, やはり無限大になるがその発散ははるかに小さいことが分かる.この点については §4-7 で触れることにする.
原子準位のシフト(Atomic level shifts)
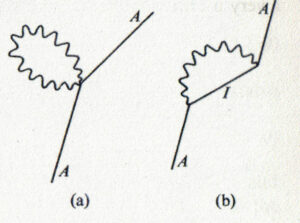
ここでは束縛された原子電子の自己エネルギーについて議論するが, それはここまで議論して来た「輻射の量子論」の枠組みの中で行ない, 横方向の電磁場は量子化するが電子は非相対論的に扱かうこととする.原子状態 \(A\) を考える(それは必ずしも安定な基底状態とは仮定しない).束縛された電子の自己エネルギーは, 量子化された輻射場との相互作用による状態 \(A\) のエネルギーシフトとして出現する.先に強調したように, 輻射の量子論によれば, たとえ入射する輻射場が無くても原子状態 \(A\) は光子を放射することが出来るのだった.そこで原子が放射された光子を吸収して状態 \(A\) に戻ったとしよう.\(e^2\) のオーダーには図 2-7 に示すように2種類の過程が存在する.
この2つの図のうち, 相互作用ハミルトニアンの \(\mb{A}\cdot\mb{A}\) 相互作用項に起因する図 2-7(a) の結果は, 原子準位のシフトの観点からは面白くないことが分かる.図 2-7(b) の基本的な摂動の行列要素は, 次の \(A\to I + \gamma\) に対する「放射」行列要素:
H^{(\mathrm{emis})}_{IA}=H’_{IA}\,e^{i\omega t}
\tag{2.223}
\end{equation}
と, 次の \(I +\gamma \to A\) に対する「吸収」行列要素:
H^{(\mathrm{abs})}_{AI}=H’_{AI}\,e^{-i\omega t}
\tag{2.224}
\end{equation}
である.ただし, 時間依存しない行列要素 \(H’_{IA}\) と \(H’_{AI}\) は, 前と同様に双極子近似を用いるとして次とする [2][訳註] 因子はFeynmanに合わせるために「Gauss単位系」に置き換えてある.:
H’_{IA}=(H’_{AI})^{*}=-c\sqrt{\frac{2\pi \hbar}{\omega}}\frac{e}{mc}\BraKet{I}{\mb{p}\cdot\mb{\epsilon}^{(\alpha)}}{A}
\tag{2.225}
\end{equation}
時間依存する振幅 \(c_I\) と \(c_A\) を求めるには, 次の連立微分方程式を解かなければならない:
&i\hbar \dot{c}_I = \sum_{\mathrm{photon}} H^{(\mathrm{emis})}_{IA}\,c_{A}\,e^{i(E_I-E_A)t/\hbar},\tag{2.226}\\
&i\hbar \dot{c}_A = \sum_{\mathrm{photon}} \sum_I H^{(\mathrm{abs})}_{AI}\,c_{I}\,e^{i(E_A-E_I)t/\hbar},
\tag{2.227}
\end{align}
量子化された場の演算子 \(\mb{A}\) は, 真空の状態と「任意の」運動量と偏光を持った単一光子状態との間に非ゼロの行列要素を持つので, 記号 \(\Sigma_{\mathrm{photon}}\) の和は「全ての可能な運動量と偏光」について取り, それは光子エネルギーが \(E_I- E_A\) に等しくない場合も含むことを意味している.
我々の関心事は状態 \(A\) のエネルギーシフトの式を得ることである.このため, 式 (2.226) と式 (2.227) を次のような前提(ansatz)で解くことを提案する:
c_A = \exp\bigl[-i\Delta E_A t/\hbar\bigr]
\tag{2.228}
\end{equation}
この前提では, 完全な波動関数は次のように変化する:
\psi \sim u_A(\mb{x})\exp\left[-i(E_A+\Delta E_A)t/\hbar\right]
\tag{2.229}
\end{equation}
従って波動関数の時間依存性は, エネルギー \((E_A+\Delta E_A)\) の量子力学的状態から期待されるものと正確に一致する.式 (2.228) を式 (2.226) に挿入して積分すると,
c_I &= \frac{1}{i\hbar}\sum_{\mathrm{photon}}\int_0^{t}H’_{IA}\exp\bigl[i\omega t’\bigr]
\exp\left[-\frac{i\Delta E_A t’}{\hbar}\right]\exp\left[\frac{i(E_I-E_A)t’}{\hbar}\right]\,dt’\notag\\
&=\sum_{\mathrm{photon}}H’_{IA}\frac{\exp\bigl[i(E_I-E_A-\Delta E_A+\hbar\omega)t/\hbar\bigr]-1}
{E_A+\Delta E_A -E_I-\hbar\omega}
\tag{2.230}
\end{align}
状態 \(A\) のエネルギーシフト \(\Delta E_A\) を求めるには, 式 (2.228) と式 (2.230) を式 (2.227) に代入する.すると左辺は,
i\hbar\dot{c}_A=i\hbar\times\left(-\frac{i}{\hbar}\right)\Delta E_A\,\exp\bigl[-i\Delta E_A t/\hbar\bigr]
=\Delta E_A\,\exp\bigl[-i\Delta E_A t/\hbar\bigr],
\end{equation*}
右辺は,
\begin{align*}
&\sum_{\mathrm{photon}} \sum_I H’_{AI}\,e^{-i\omega t}H’_{IA}\frac{\exp\bigl[i(E_I-E_A-\Delta E_A+\hbar\omega)t/\hbar\bigr]-1}
{E_A+\Delta E_A -E_I-\hbar\omega}\,e^{i(E_A-E_I)t/\hbar}\\
&=\sum_{\mathrm{photon}} \sum_I \bigl|H’_{IA}\bigr|^{2}\,
\frac{\exp\bigl[-i\Delta E_A t/\hbar\bigr]-\exp\bigl[i(E_A-E_I-\hbar\omega)t/\hbar\bigr]}{E_A+\Delta E_A -E_I-\hbar\omega}
\end{align*}
従って両辺を \(\exp\bigl[-i\Delta E_A t/\hbar\bigr]\) で割れば,
\Delta E_A = \sum_{\mathrm{photon}}\sum_I \bigl|H’_{IA}\bigr|^{2}
\frac{1-\exp\bigl[i(E_A+\Delta E_A-E_I-\hbar\omega)t/\hbar\bigr]}{E_A+\Delta E_A-E_I-\hbar\omega}
\tag{2.231}
\end{equation}
\(\Delta E_A\) を \(e\) の2次で計算しているので, 式 (2.231) の右辺の \(\Delta E_A\) を削除するのは正当なことである.従って,
\Delta E_A = \sum_{\mathrm{photon}}\sum_I \bigl|H’_{IA}\bigr|^{2}
\frac{1-\exp\bigl[i(E_A-E_I-\hbar\omega)t/\hbar\bigr]}{E_A-E_I-\hbar\omega}
\tag{2.232}
\end{equation}
ここで, 摂動が作用する時間間隔 \([0,t]\) を無限大にすることが出来る.しかし, そのままでは(as it stands) この式は \(t\to\infty\) のとき振動することを示している.
それは, 式 (2.232) を次のような積分から求めたのだから当然である (式 (2.230) を参照):
\int_0^{t}e^{ixt’}\,dt’,\quad\mathrm{where}\quad x=(E_I-E_A-\Delta E_A+\hbar\omega)/\hbar
\tag{2.233}
\end{equation}
これは \(t\to \infty\) のとき明らかに不適切な定義である.しかしながら, このような積分は \(x\) に小さな正の虚部を加えることで収束させることが出来る.このようにして, 一連の非常に便利な関係が得られる [3][訳註] 次が成り立つことを用いている (砂川重信:「量子力学」の第2章 §1 (3) デルタ関数 を参照すべし): \begin{equation*} -i\int_{0}^{\infty}e^{ixt}\,dt … Continue reading:
\lim_{t\to\infty}\frac{1-e^{ixt}}{x}&=\lim_{\epsilon \to 0+}\left(-i\int_{0}^{\infty}e^{i(x+i\epsilon)t’}\,dt’\right)
=\lim_{\epsilon\to 0+}\frac{1}{x+i\epsilon}\notag\\
&=\lim_{\epsilon\to0+}\left[\frac{x}{x^{2}+\epsilon^{2}}-\frac{i\epsilon}{x^{2}+\epsilon^{2}}\right]\notag\\
&=\frac{1}{x}-i\pi\,\delta(x)
\tag{2.234}
\end{align}
これらは \(t\to\infty\) とした式 (2.232) に直に当てはめることが出来る [4][訳註] \(x=(E_A-E_I-\hbar\omega)/\hbar\) の場合であるから, \begin{align*} \Delta E_A &=\sum_{\mathrm{photon}}\sum_I … Continue reading.
するとエネルギーシフト \(\Delta E_A\) は, 実数部 \(\mathrm{Re}(\Delta E_A)\) と虚数部 \(\mathrm{Im}(\Delta E_A)\) の両方を持っていることが分かる:
&\Delta E_A=\mathrm{Re}(\Delta E_A)+i\,\mathrm{Im}(\Delta E_A),\notag\\
&\quad \mathrm{Re}(\Delta E_A) = \sum_{\mathrm{photon}}\sum_I \frac{\bigl|H’_{IA}\bigr|^{2}}{E_A-E_I-\hbar\omega}\tag{2.235}\\
&\quad \mathrm{Im}(\Delta E_A) = -\pi \sum_{\mathrm{photon}}\sum_I\, \bigl|H’_{IA}\bigr|^{2}\,\delta(E_A-E_I-\hbar\omega)
\tag{2.236}
\end{align}
式 (2.235) の光子の和は全ての運動量と偏光の光子を対象としており, 式(2.235) の原子エネルギー準位の和 \(\sum_I\) もやはり「\(E_I<E_A\) を満たす必要がない」という意味で無制限的である (「実際の」放射過程とは対照的である).つまり, 式 (2.235) の光子の放射と吸収は一般にエネルギー保存を満たさないので,「実光子(actual photon)」の放射と吸収の過程 (§ 2-4 で議論した) とは異なるものである.このような光子は「仮想的(virtual)」と言われる.物理的な原子は, 一部の時間では「原子+仮想光子」という解離状態にあると想像しても良いであろう.エネルギーシフトの実部を引き起こすのは,「全ての可能な運動量と偏極を持った仮想光子のエネルギー非保存的な放射および吸収」に関連した相互作用エネルギーである.
式 (2.235) の光子和とは対照的に, 式 (2.236) の光子和はエネルギー保存 \(E_A=E_I+\hbar\omega\) を満たす光子のみを対象としている. 言い換えれば, 式 (2.236) に現れる光子は「実光子」であって,「仮想光子」ではない.エネルギーシフト \(\Delta E_A\) が虚部を持つのは, エネルギー保存に違反することなく, 状態 \(A\) が自然放射によって状態 \(I\) に崩壊することが可能な場合だけである.より定量的には, 式 (2.236) の両辺に \(-2/\hbar\) を掛け合わせた次式に注意する:
-\frac{2}{\hbar}\mathrm{Im}\bigl(\Delta E_A\bigr) =\sum_{\mathrm{photon}}\sum_I \frac{2\pi}{\hbar}\bigl|H’_{IA}\bigr|^{2}\, \delta(E_A-E_I-\hbar\omega)
\tag{2.237}
\end{equation}
しかしこの式の右辺は正に, エネルギー的に許容される全ての最終状態を合計し「黄金律」に従って計算した自然放射の遷移確率の式である [式(2.114)から式(2.117)を参照] [5][訳註] 「遷移率」すなわち単位時間当りの遷移確率 \([w]_{i\to[n]}\) は, 時間を含む1次の摂動論が有効なとき, \begin{equation*} w_{i\to … Continue reading.従って, それは状態 \(A\) の平均寿命 \(\tau_A\) の逆数に等しい.よって, 次のような重要な結果が得られる:
-\frac{2}{\hbar}\mathrm{Im}\bigl(\Delta E_A\bigr) = \frac{1}{\tau_A}=\frac{\Gamma_A}{\hbar},\quad\rightarrow\quad \mathrm{Im}\bigl(\Delta E_A\bigr) =-\frac{\Gamma_A}{2}
\tag{2.238}
\end{equation}
今や \(\mathrm{Im}\,[\Delta E_A]\) の物理的意義(重要性)は明らかである.式 (2.229) に戻ると, 完全な波動関数は次で与えられることが分かる:
\psi &\sim u_A(\mb{x})\exp\left[-i(E_A+\Delta E_A)t/\hbar\right]\notag\\
&=u_A(\mb{x})\exp\left[-i(E_A+\mathrm{Re}[\Delta E_A]+i\mathrm{Im}[\Delta E_A])t/\hbar\right]\notag\\
&=u_A(\mb{x})\exp\left[-\frac{i(E_A+\mathrm{Re}[\Delta E_A])t}{\hbar}+\mathrm{Im}[\Delta E_A]\frac{t}{\hbar}\right]\notag\\ &=u_A(\mb{x})\,\exp\left[-\frac{i(E_A+\mathrm{Re}[\Delta E_A])t}{\hbar}-\frac{\Gamma_A t}{2\hbar}\right]
\tag{2.239}
\end{align}
ここから, おなじみの結論が導かれる:不安定な状態 \(A\) を見出す確率は次式のように減衰する [6][訳註] 自発崩壊をする独立な系がたくさんあるとき, 系が崩壊せずに存続する時間の統計的平均値, 又は未崩壊の系が \(1/e\) … Continue reading:
\bigl|\psi\bigr|^{2} \sim e^{-\Gamma_A t/\hbar}
\tag{2.240}
\end{equation}
要約すると, エネルギーシフト \(\Delta E_A\) の実数部(仮想光子の放射と吸収から生じる)は, 我々が通常「準位のずれ」と呼んでいるものであり, そして \(\Delta E_A\) の虚数部(実光子の放射と吸収から生じる)は, 問題としている不安定状態の崩壊幅, すなわち寿命の逆数を特徴づけるものである.また, 微分方程式 (2.181) の第2項が \(\Delta E_A\) の虚数部から生じると見做せるので, 前に §2-6 で述べた放射減衰の現象論的な取り扱いが今や正当化されることになるにも注意する.
以降は \(\Delta E_A\) の実数部のみに注目する.(これ以降 \(\Delta E_A \)という表現は, 実数部を意味するものとする).式 (2.225) を式 (2.235) に挿入すると次のようになる:
\begin{align*}
\Delta E_A &=\sum_{\mathrm{photon}}\sum_I \frac{\bigl|H’_{IA}\bigr|^{2}}{E_A-E_I-\hbar\omega}\\
&=\sum_{\mathrm{photon}}\sum_I \frac{2\pi\hbar c^{2}}{\omega}\left(\frac{e}{mc}\right)^{2} \bigl|(\mb{p}\cdot\mb{\epsilon}^{(\alpha)})_{IA}\bigr|^{2}\frac{1}{E_A-E_I-\hbar\omega}
\end{align*}
ここで光子和 \(\sum_{\mathrm{photon}}\) は「全ての運動量 \(\mb{p}\) (または波数 \(\mb{k}\)) と偏極 \(\alpha\) を持った光子の和」を表しているので次のように置き換える:
\sum_{\mathrm{photon}}=\sum_{\mb{p}}\sum_{\alpha}\ \rightarrow\ \int \frac{d^{3}\mb{p}}{(2\pi\hbar)^{3}}\sum_{\alpha} =\int \frac{d^{3}\mb{k}}{(2\pi)^{3}}\sum_{\alpha}
\end{equation*}
従って [7][訳註] \(\mb{k}\) 空間に於ける体積積分は \(k=|\mb{k}|\) そして \(dE_{\gamma}=d(\hbar\omega)=d(\hbar k c)=\hbar c dk\) および \(k^{2}=(\omega/c)^{2}\) … Continue reading,
\begin{align*}
\Delta E_A &=\sum_{\mb{p}}\sum_{\alpha}\sum_I \frac{2\pi\hbar c^{2}}{\omega}\left(\frac{e}{mc}\right)^{2} \bigl|(\mb{p}\cdot\mb{\epsilon}^{(\alpha)})_{IA}\bigr|^{2}\frac{1}{E_A-E_I-\hbar\omega}\\
&=\int \frac{d^{3}\mb{k}}{(2\pi)^{3}}\sum_I \frac{2\pi\hbar c^{2}}{\omega}\left(\frac{e}{mc}\right)^{2} \sum_{\alpha}\bigl|(\mb{p}\cdot\mb{\epsilon}^{(\alpha)})_{IA}\bigr|^{2}\frac{1}{E_A-E_I-\hbar\omega}\\
&= 2\pi\hbar c^{2}\left(\frac{e}{mc}\right)^{2}\sum_I \int \frac{d^{3}\mb{k}}{(2\pi)^{3}}\frac{1}{\omega} \frac{1}{E_A-E_I-\hbar\omega}\sum_{\alpha}\bigl|(\mb{p}\cdot\mb{\epsilon}^{(\alpha)})_{IA}\bigr|^{2}\\
&=\frac{2\pi\hbar c^{2}}{(2\pi)^{3}}\left(\frac{e}{mc}\right)^{2}\sum_I \int dE_{\gamma}\,\frac{\omega^{2}}{\hbar c^{3}} \frac{1}{\omega}\frac{1}{E_A-E_I-\hbar\omega} \int d\Omega \sum_{\alpha}\bigl|(\mb{p}\cdot\mb{\epsilon}^{(\alpha)})_{IA}\bigr|^{2} \end{align*}
ただし \(E_{\gamma}=\hbar\omega=\hbar|\mb{k}|c\) である.そこで \(\displaystyle \frac{\omega^{2}}{\hbar c^{3}}\frac{1}{\omega}=\frac{\omega}{\hbar c^{3}}=\frac{\hbar\omega}{\hbar^{2}c^{3}}=\frac{E_{\gamma}}{\hbar^{2}c^{3}}\) とすれば,
\Delta E_A &=\frac{\hbar c^{2}}{(2\pi)^{2}}\frac{e^{2}}{m^{2}c^{2}}\sum_I \int dE_{\gamma}\,\frac{E_{\gamma}}{\hbar^{2}c^{3}} \frac{1}{E_A-E_I-\hbar\omega}\int d\Omega \sum_{\alpha}\bigl|(\mb{p}\cdot\mb{\epsilon}^{(\alpha)})_{IA}\bigr|^{2}\notag\\ &=\frac{1}{(2\pi)^{2}}\left(\frac{e^{2}}{\hbar c}\right)\frac{1}{(mc)^{2}}\sum_I \int dE_{\gamma}\,
\frac{E_{\gamma}}{E_A-E_I-\hbar\omega}\int d\Omega \sum_{\alpha}\bigl|(\mb{p}\cdot\mb{\epsilon}^{(\alpha)})_{IA}\bigr|^{2}
\tag{2.241}
\end{align}
偏光和と角度積分は, 以前の自然放射に関する議論と同じであり (式 (2.130) から式 (2.132) を参照),
\int d\Omega\,\sum_{\alpha}\,\bigl|(\mb{p}\cdot\mb{\epsilon}^{(\alpha)})_{IA}\bigr|^{2} = \frac{8\pi}{3}\bigl|(\mb{p})_{IA}\bigr|^{2} \tag{2.242}
\end{equation}
従って, 残るのはエネルギー積分だけである [8][訳註] この式(2.243)の2番目の因子は「微細構造因子」\(\displaystyle \alpha=\frac{e^{2}}{\hbar c}\)であることに注意する.:
\Delta E_A =\frac{2}{3\pi}\left(\frac{e^{2}}{\hbar c}\right)\frac{1}{(mc)^{2}} \sum_I \int \frac{E_{\gamma}\bigl|(\mb{p})_{IA}\bigr|^{2}}{E_A-E_I-E_{\gamma}}\,dE_{\gamma}
\tag{2.243}
\end{equation}
このエネルギー積分は \(E_{\gamma}\) のゼロから無限大までの全ての可能な値にわたって行なう.しかし, 積分は明らかに線形に発散する.電子の非相対論的近似は \(E_{\gamma}>mc^{2}\) の光子の放出に対しては破綻せざるを得ないので, 非常に高いエネルギーの仮想光子からの寄与をあまり深刻に考えることは出来ないと主張することが出来る.従って, 次のように置き換える:
\int_{0}^{\infty}dE_{\gamma}\quad \rightarrow\quad \int_{0}^{E_{\gamma}^{\mathrm{(max)}}} dE_{\gamma}
\tag{2.244}
\end{equation}
ただし \(E_{\gamma}^{\mathrm{(\max)}}\) は「カットオフ エネルギー」(cut-off energy) として知られている量である.残念ながら, この方法で計算されたエネルギーシフトは我々が導入した任意パラメータ \(E_{\gamma}^{\mathrm{(max)}}\) に非常に敏感である.
質量の繰り込み(Mass renormalization)
この段階で, 図 2-7(b) に示した過程による運動量 \(\mb{p}\) が固定された「自由電子の自己エネルギー」について議論しておくと有利であろう.今度は自由電子なので, 状態 \(A\) と状態 \(I\) の波動関数は各々 \(\psi_A(\mb{x})\equiv\psi_{\mb{p}}=e^{i\mb{p}\cdot\mb{x}/\hbar}/\sqrt{V}\) と \(\psi_I(\mb{x})\equiv \psi_{\mb{p}’}=e^{i\mb{p}’\cdot\mb{x}/\hbar}/\sqrt{V}\) で表される.従って, 式 (2.235) 中の時間に依存しない摂動の行列要素 \(H’_{IA}\) は,「自由電子による光子の自発放射であるから, 式 (2.99) の \(H_{\mathrm{int}}\) に於いて輻射場起因の因子 \(e^{i\omega t}\) を省き \(n_{\mb{k},\alpha}\) をゼロと置いた式で更に \(i=1,B=I\) とした場合」である.よって,
\begin{align*}
\BraKet{B;n_{\mb{k},\alpha}+1}{H_{\mathrm{int}}}{A,n_{\mb{k},\alpha}}&=-\frac{e}{m}\sqrt{\frac{(n_{\mb{k},\alpha}+1)2\pi\hbar}{\omega V}}
\sum_{i}\BraKet{B}{e^{-i\mb{k}\cdot\mb{x}_i}\mb{p}_i\cdot\mb{\epsilon}^{(\alpha)}}{A}e^{i\omega t},\tag{2.99}\\
\rightarrow\ H’_{IA}=e^{-i\omega t}\BraKet{I}{H_{\mathrm{int}}}{A}
&=-\frac{e}{m}\sqrt{\frac{2\pi\hbar}{\omega V}}\,\int \psi^{*}_I(\mb{x})\,e^{-i\mb{k}\cdot\mb{x}}\,\mb{p}\cdot\mb{\epsilon}^{(\alpha)}
\,\psi_A(\mb{x})\,d^{3}\mb{x}\\
&=-\frac{e}{m}\sqrt{\frac{2\pi\hbar}{\omega V}}\int \frac{e^{-i\mb{p}’\cdot\mb{x}/\hbar}}{\sqrt{V}}\,
e^{-i\hbar\mb{k}\cdot\mb{x}/\hbar}\bigl(\mb{p}\cdot\mb{\epsilon}^{(\alpha)}\bigr)\,\frac{e^{i\mb{p}\cdot\mb{x}/\hbar}}{\sqrt{V}}\,d^{3}x\\
&=-\frac{e}{m}\sqrt{\frac{2\pi\hbar}{\omega V}}\bigl(\mb{p}\cdot\mb{\epsilon}^{(\alpha)}\bigr)
\int_V \frac{e^{-i\mb{p}’\cdot\mb{x}/\hbar}}{\sqrt{V}}\cdot\frac{e^{i(\mb{p}-\hbar\mb{k})\cdot\mb{x}/\hbar}}{\sqrt{V}}\,d^{3}x\\
&=-\frac{e}{m}\sqrt{\frac{2\pi\hbar}{\omega V}}\bigl(\mb{p}\cdot\mb{\epsilon}^{(\alpha)}\bigr)
\BK{\psi_{\mb{p}’}}{\psi_{\mb{p}-\hbar\mb{k}}}
\end{align*}
\(\BK{\psi_{s}}{\psi_{s’}}=\delta_{s\,s’}\) であるから,
H’_{IA}=-\sqrt{\frac{2\pi\hbar}{\omega V}}\,\frac{e}{m}\,\mb{p}\cdot\mb{\epsilon}^{(\alpha)}\,
\delta_{\mb{p}’,\,\mb{p}-\hbar\mb{k}}
\tag{2.245}
\end{equation}
電子が非相対論的に扱えるエネルギー範囲に於いて, エネルギー分母は \(\hbar\mb{k}\ll\mb{p}\) として次のように近似できる:
E_A-E_I-\hbar\omega = \frac{\mb{p}^{2}}{2m}-\frac{(\mb{p}-\hbar\mb{k})^{2}}{2m}-\hbar\omega
\approx \frac{\mb{p}^{2}}{2m}-\frac{\mb{p}^{2}}{2m}-\hbar\omega = -\hbar\omega
\tag{2.246}
\end{equation}
残りのステップは前と同じである.上式から, 式 (2.243) に於いて \(E_A-E_I-E_{\gamma}\sim -E_{\gamma}\) とすれば,
\begin{align*}
\Delta E_A &=\frac{2}{3\pi}\left(\frac{e^{2}}{\hbar c}\right)\frac{1}{(mc)^{2}}
\sum_I \int \frac{E_{\gamma}\bigl|(\mb{p})_{IA}\bigr|^{2}\,dE_{\gamma}}{E_A-E_I-E_{\gamma}}
=\frac{2}{3\pi}\left(\frac{e^{2}}{\hbar c}\right)\frac{1}{(mc)^{2}}
\sum_I \int \frac{E_{\gamma}\bigl|(\mb{p})_{IA}\bigr|^{2}\,dE_{\gamma}}{-E_{\gamma}}\\
&=-\frac{2}{3\pi}\left(\frac{e^{2}}{\hbar c}\right)\frac{1}{(mc)^{2}}\int \sum_I\bigl|(\mb{p})_{IA}\bigr|^{2}\,dE_{\gamma}
=-\frac{2}{3\pi}\left(\frac{e^{2}}{\hbar c}\right)\frac{1}{(mc)^{2}}\int \bigl(\mb{p}^{2}\bigr)_{AA}\,dE_{\gamma}\\
&=-\left(\frac{e^{2}}{\hbar c}\right)\frac{2}{3\pi}\frac{\bigl(\mb{p}^{2}\bigr)_{AA}}{(mc)^{2}}\int dE_{\gamma},
\qquad \bigl(\mb{p}^{2}\bigr)_{AA}=\mb{p}^{2}
\end{align*}
よって,「自由電子の自己エネルギー」として次を得る:
&\Delta E_{\mathrm{free}}=-\left(\frac{e^{2}}{\hbar c}\right)\frac{2\mb{p}^{2}}{3\pi(mc)^{2}}
\int_{0}^{E_{\gamma}^{\mathrm{(max)}}} dE_{\gamma}=C\,\mb{p}^{2},\tag{2.247}\\
&\qquad \mathrm{where}\qquad
C = -\left(\frac{e^{2}}{\hbar c}\right)\frac{2}{3\pi}\frac{E_{\gamma}^{\mathrm{(max)}}}{(mc)^{2}}
=-\alpha \frac{2}{3\pi}\frac{E_{\gamma}^{\mathrm{(max)}}}{m^{2}c^{2}}
\tag{2.248}
\end{align}
この式 (2.247) もやはり \(E_{\gamma}^{\mathrm{(max)}}\to\infty\) のとき線形に発散することに注意する.
自由電子の場合の図 2-7(b) は, 単純に \(\mb{p}^{2}\) に比例するエネルギーを生じることが分かる.電磁相互作用のスイッチを決して切ることが出来ない程度に, 通常の運動エネルギー項 \(\mb{p}^{2}/2m\) からこの追加エネルギーを分離することは出来ない.実際, 観測可能な運動エネルギーは, 図 2-7(b) のような相互作用が存在しない仮想世界の運動エネルギーと我々が計算した \(C\mb{p}^{2}\) との和である.一方, 電子を非相対論的な粒子と見做すと, 電子の質量はエネルギー運動量の関係式
\ppdiff{E}{\mb{p}^{2}}=\frac{1}{2m}
\tag{2.249}
\end{equation}
で与えられる.ただし \(E\) は自由粒子のエネルギーである.従って, 観測される電子質量 \(m_{\mathrm{obs}}\) は, 次式に従って \(C\) と関係している:
\frac{\mb{p}^{2}}{2m_{\mathrm{obs}}}&=\frac{\mb{p}^{2}}{2m_{\mathrm{bare}}}+C\mb{p}^{2}
=\frac{\mb{p}^{2}}{2m_{\mathrm{bare}}}+\frac{2m_{\mathrm{bare}}C \mb{p}^{2}}{2m_{\mathrm{bare}}}
=\frac{\mb{p}^{2}}{2m_{\mathrm{bare}}}\left(1+2m_{\mathrm{bare}}C\right)\notag\\
&=\frac{\mb{p}^{2}}{2m_{\mathrm{bare}}(1+2m_{\mathrm{bare}}C)^{-1}}
\approx \frac{\mb{p}^{2}}{2m_{\mathrm{bare}}(1-2m_{\mathrm{bare}}C)}
\tag{2.250}
\end{align}
ただし \(m_{\mathrm{bare}}\) は, 図 2-7(b) で表される相互作用がない場合に測定される電子の質量を表わす.要するに, 図 2-7(b) の正味の効果は電子質量の定義を変えただけである:
m_{\mathrm{bare}}\ \rightarrow\ m_{\mathrm{obs}}\approx m_{\mathrm{bare}}(1-2mC)
=\left[1+\left(\frac{1}{137}\right)\frac{4}{3\pi}
\frac{E_{\gamma}^{\mathrm{(max)}}}{mc^{2}}\right]\,m_{\mathrm{bare}}
\tag{2.251}
\end{equation}
我々が実験室で観測している質量は \(m_{\mathrm{bare}}\) ではなくて, 時には「繰り込み質量」(renormalized mass) と呼ばれることがある \(m_{\mathrm{obs}}\) である [9]固体物理学に詳しい読者であれば, 輻射の量子論に於ける「観測質量」または「繰り込み質量」の概念が, … Continue reading.式 (2.247) の \(\Delta E^{\mathrm{(free)}}\) は負であるのに対し \(\Delta m=m_{\mathrm{obs}}-m_{\mathrm{bare}}\) は正であることに注意する.式 (2.251) から \(E^{\mathrm{(max)}}_{\gamma}\) を \(mc^{2}\) のオーダーで「カットオフ」した場合, 観測される電子質量の約 0.3 % が自己エネルギーに起因することが分かる.しかし, このような計算に大きな意味を見出すことはできない.なぜなら, ディラックの相対論的電子理論を用いると, 電子の自己エネルギーは全く異なる式になるからである.
ここで「原子状態の準位シフト」に話を戻そう.Schrödinger 程式を解いて原子のエネルギー準位を計算するときに用いる運動エネルギーは \(\mb{p}^{2}/2m_{\mathrm{obs}}\) であり, これにはすでに補正項 \(C\mb{p}^{2}\) が含まれている!.観測可能なエネルギーシフトを見積もる際には, すでに考慮に入れたエネルギー部分を必ず差し引かなければならない.なぜなら, 無摂動のエネルギー準位を計算する際には \(\mb{p}^{2}/2m_{\mathrm{obs}}\) ではなく \(\mb{p}^{2}/2m_{\mathrm{bare}}\) を用いるからである.これが H.A.Kramers によって提唱された「質量繰り込み」の考え方である.定量的には, 観測可能なエネルギーシフト \(\Delta E_A^{(\mathrm{obs})}\) は次式で与えられる:
\Delta E_A^{(\mathrm{obs})}&=\Delta E_A – \BraKet{A}{\left(\frac{\mb{p}^{2}}{2m_{\mathrm{obs}}}
-\frac{\mb{p}^{2}}{2m_{\mathrm{bare}}}\right)}{A}=\Delta E_A – \BraKet{A}{C\mb{p}^{2}}{A}\notag\\
&=\Delta E_A – C\BraKet{A}{\mb{p}^{2}}{A}
\tag{2.252}
\end{align}
言い換えれば, 観測可能なのは「束縛電子の自己エネルギーと自由電子の自己エネルギーの差」である.
References
| ↑1 | Jackson (1962), pp. 578-597. |
|---|---|
| ↑2 | [訳註] 因子はFeynmanに合わせるために「Gauss単位系」に置き換えてある. |
| ↑3 | [訳註] 次が成り立つことを用いている (砂川重信:「量子力学」の第2章 §1 (3) デルタ関数 を参照すべし): \begin{equation*} -i\int_{0}^{\infty}e^{ixt}\,dt =\left.\frac{e^{ixt}}{x}\right|_{\infty}^{0} =\frac{1}{x}-\left(\frac{e^{ixt}}{x}\right)_{t\to\infty}=\lim_{t\to\infty}\frac{1-e^{ixt}}{x},\qquad \delta(x)=\frac{1}{\pi}\lim_{\epsilon\to0}\frac{\epsilon}{x^{2}+\epsilon^{2}} \end{equation*} |
| ↑4 | [訳註] \(x=(E_A-E_I-\hbar\omega)/\hbar\) の場合であるから, \begin{align*} \Delta E_A &=\sum_{\mathrm{photon}}\sum_I \frac{\bigl|H’_{IA}\bigr|^{2}}{\hbar}\left(\frac{1}{x}-i\pi\,\delta(x)\right) =\sum_{\mathrm{photon}}\sum_I \frac{\bigl|H’_{IA}\bigr|^{2}}{\hbar}\left(\frac{\hbar}{E_A-E_I-\hbar\omega}-i\pi \hbar\, \delta(E_A-E_I-\hbar\omega)\right)\\ &=\sum_{\mathrm{photon}}\sum_I \frac{\bigl|H’_{IA}\bigr|^{2}}{E_A-E_I-\hbar\omega}-i\sum_{\mathrm{photon}}\sum_I \pi\,\bigl|H’_{IA}\bigr|^{2}\, \delta(E_A-E_I-\hbar\omega) \end{align*} |
| ↑5 | [訳註] 「遷移率」すなわち単位時間当りの遷移確率 \([w]_{i\to[n]}\) は, 時間を含む1次の摂動論が有効なとき, \begin{equation*} w_{i\to [n]}=\frac{2\pi}{\hbar}\bigl|V_{ni}\bigr|^{2}\,\delta(E_n-E_i) \end{equation*} と書ける.この式は「フェルミの黄金則」と呼ばれ, 実際上非常に重要である. |
| ↑6 | [訳註] 自発崩壊をする独立な系がたくさんあるとき, 系が崩壊せずに存続する時間の統計的平均値, 又は未崩壊の系が \(1/e\) になる時間を「平均寿命」と言う.平均寿命は「崩壊定数」の逆数である.統計理論によると \(dt\) 時間中に原子核が崩壊する確率は \(\lambda dt\) である.最初に崩壊していない原子核が \(N_0\) 個あったとき \(dt\) 時間内に崩壊する数 \(dN\) は \(dN=-\lambda dt\cdot N\) で与えられるから, これを積分すると時刻 \(t\) に存在する原子数 \(N\) は \(N=N_0\,e^{-\lambda t}\) となる.このときの \(\lambda\) を「崩壊定数」という. |
| ↑7 | [訳註] \(\mb{k}\) 空間に於ける体積積分は \(k=|\mb{k}|\) そして \(dE_{\gamma}=d(\hbar\omega)=d(\hbar k c)=\hbar c dk\) および \(k^{2}=(\omega/c)^{2}\) として次のように書ける: \begin{equation*} \int d^{3}\mb{k}=\iint k^{2}dk\,d\Omega = \int k^{2}\,dk\int d\Omega =\int k^{2}\frac{dE_{\gamma}}{\hbar c}\int d\Omega =\int dE_{\gamma}\,\frac{\omega^{2}}{\hbar c^{3}}\int d\Omega \end{equation*} |
| ↑8 | [訳註] この式(2.243)の2番目の因子は「微細構造因子」\(\displaystyle \alpha=\frac{e^{2}}{\hbar c}\)であることに注意する. |
| ↑9 | 固体物理学に詳しい読者であれば, 輻射の量子論に於ける「観測質量」または「繰り込み質量」の概念が, 固体の格子振動と相互作用する電子の「有効質量」(effective mass)の概念に似ていることにお気付きだろう. |