\(\)
QEDの第12講の準備として, 「一様に動いている点電荷」が生成する 電場 \(\mathbf{E}\) と磁場 \(\mathbf{H}\) に対して
\def\mb#1{\mathbf{#1}}
\mb{H}=\frac{1}{c}\mb{v}\times\mb{E}
\end{equation*}
が成り立つことを, オッペンハイマー:「電気力学」の§11の文章を抜粋して示しておく [1][ブログ註] この文章とほぼ同じものが, 砂川重信:「理論電磁気学」の第9章§3に例題として書かれているので, 参照することをお勧めする. .
11. 一様に動いている点電荷の場
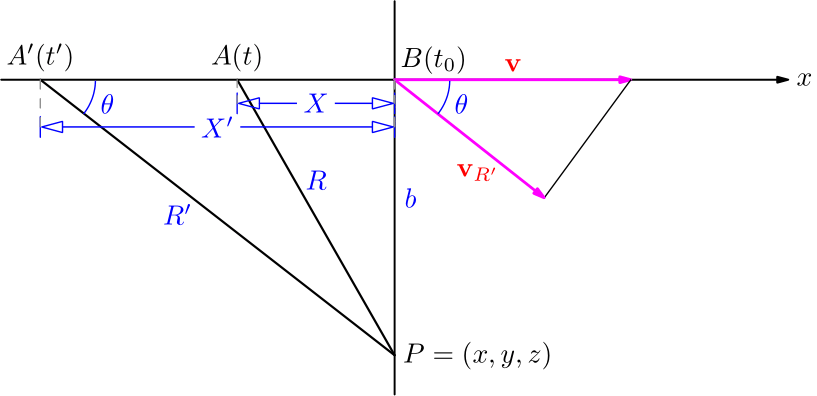
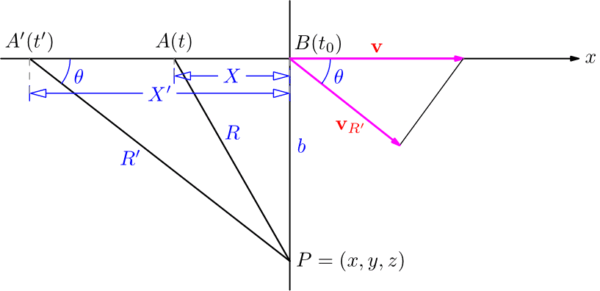
電荷 \(e\) が \(x\) 軸に沿って正の方向へ一様な速さ \(v\) で動いているものとする.このとき, その電荷の運動の軌道から垂直距離 \(b\) だけ離れている空間の1点\(P\)に於ける場を求めたいのである.
電荷が時刻 \(t\) に於いて上図 1. の点 \(A\) に存在するときに, その時刻に於ける点 \(P\) の場を計算しよう.以下,「遅延した」(retarded) 物理量にはダッシュを付けることにする.電荷が \(B\) 点に達するときの時刻を \(t_0\) とすると, 電荷が \(A\) に居る時, 点 \(P\) に到着する電磁波は点 \(A’\) を出発したものである.従ってその間に時間は \(t-t’\) だけ経過しているから距離 \(R’\) は \(R’=c(t-t’)\) である.また区間 \(\overline{A’B}=X’\) は電荷 \(e\) が速さ \(v\) で時間 \((t_0-t’)\) の間に走る距離である.よって, 次式が成り立つ:
\def\ds#1{\mbox{${\displaystyle\strut #1}$}}
\def\ppdiff#1#2{\frac{\partial #1}{\partial #2}}
R’^{2}=c^{2}(t-t’)^{2}=X’^{2}+b^{2}=v^{2}(t_0-t’)^{2}+b^{2}
\tag{11.1}
\end{equation}
また, 速度の \(R’\) 方向の成分 \(v_{R’}\) は, 角度 \(\angle BA’P=\theta\) とすると \(\displaystyle \cos\theta=\frac{v_{R’}}{v}=\frac{X’}{R’}\) が言えるから, 次で与えられる:
v_{R’}=\frac{X’}{R’}v\quad\rightarrow\quad \frac{v_{R’}}{c}=\frac{X’}{R’}\frac{v}{c}\quad
\mathrm{or,}\quad
R’\frac{v_{R’}}{c}=\frac{v}{c}X’
\tag{11.2}
\end{equation}
これらの式を使って「Liénard-Wiechert のポテンシャル」を各瞬間の量で計算することが出来る.
式 (11.1) から,
c^{2}(t’-t)^{2}=v^{2}(t’-t_0)^{2}+b^{2}
\end{equation*}
であり, 従ってこの2次方程式の解として次が得られる:
t’=\frac{c^{2}t-v^{2}t_0\pm\sqrt{c^{2}v^{2}(t_0-t)^{2}+(c^{2}-v^{2})b^{2}}}{(c^{2}-v^{2})}
\end{equation*}
この2個の解の中で遅延の時間を与えるものとしては, 負号の方をとらなければならない [2][ブログ註] この解の式を近似し, 分母の \(v^{2}\) と分子の根号内の \((c^{2}-v^{2})b^{2}\) を微小として省略するなどすると, \begin{equation*} t’ \sim … Continue reading:
t’=\frac{c^{2}t-v^{2}t_0-\sqrt{c^{2}v^{2}(t_0-t)^{2}+(c^{2}-v^{2})b^{2}}}{(c^{2}-v^{2})}
\end{equation*}
この式から, 次式が得れる:
\begin{align*}
X’=v(t_0-t’)\quad&\rightarrow\quad \frac{X’}{v}=t_0-t’=\frac{c^{2}(t_0-t)+\sqrt{c^{2}v^{2}(t_0-t)^{2}+(c^{2}-v^{2})b^{2}}}{c^{2}-v^{2}},\\
R’=c(t-t’)\quad&\rightarrow\quad \frac{R’}{c}=t-t’=\frac{v^{2}(t_0-t)+\sqrt{c^{2}v^{2}(t_0-t)^{2}+(c^{2}-v^{2})b^{2}}}{c^{2}-v^{2}}
\end{align*}
ところが, 上式から
\begin{align*}
R’-\frac{v}{c}X’&=c(t-t’)-\frac{v}{c}v(t_0-t’)\\
&=ct-ct’-\frac{v^{2}}{c}t_0+\frac{v^{2}}{c}t’=-\frac{t'(c^{2}-v^{2})}{c}+ct-\frac{v^{2}}{c}t_0\\
&=-\frac{1}{c}\left\{c^{2}t-v^{2}t_0-\sqrt{c^{2}v^{2}(t_0-t)^{2}+(c^{2}-v^{2})b^{2}}\right\}
+ct-\frac{v^{2}}{c}t_0\\
&=\frac{1}{c}\sqrt{c^{2}v^{2}(t_0-t)^{2}+(c^{2}-v^{2})b^{2}}
=\sqrt{v^{2}(t_0-t)^{2}+\left(1-\frac{v^{2}}{c^{2}}\right)b^{2}}
\end{align*}
よって, 次式が言える:
R^{*}\equiv R’-\frac{v}{c}X’=\sqrt{v^{2}(t_0-t)^{2}+\left(1-\frac{v^{2}}{c^{2}}\right)b^{2}}
\tag{11.3}
\end{equation*}
すると Liénard-Wiechert のスカラーポテンシャル \(\phi\) 及び ベクトルポテンシャル \(\mb{A}\) とはそれぞれ, 式 (11.2) の関係:\(\displaystyle R’\frac{v_{R’}}{c}=\frac{v}{c}X’\) と式 (11.3) を用いることで次のように与えられる:
\begin{align*}
\phi &=\left.\frac{e}{\ds{R\left(1-\frac{v_R}{c}\right)}}\right|_{\mathrm{ret}}
=\frac{e}{\ds{R’-\frac{v_{R’}}{c}R’}}
=\frac{e}{\ds{R’-\frac{v}{c}X’}}=\frac{e}{R^{*}}\tag{11.4}\\
\mb{A}&=\left.\frac{e\mb{v}/c}{\ds{R\left(1-\frac{v_R}{c}\right)}}\right|_{\mathrm{ret}}
=\frac{e\mb{v}/c}{\ds{R’-\frac{v_{R’}}{c}R’}}
=\frac{e\mb{v}/c}{\ds{R’-\frac{v}{c}X’}}
=\frac{e\mb{v}}{cR^{*}}
\tag{11.5}
\end{align*}
点 \(P\) のデカルト座標を \((x,y,z)\) とし, 電荷が原点にあるときに \(t=0\) となるように時間の原点を取ると次が言える:
x=vt_0,\quad y^{2}+z^{2}=b^{2},\quad \therefore\quad
R^{*}=\sqrt{(x-vt)^{2}+\left(1-\frac{v^{2}}{c^{2}}\right)(y^{2}+z^{2})}
\end{equation*}
以上の式を用いると, 場の量は単に微分をすることによって得られる.すなわち3個のベクトル \(\mb{a}_x,\mb{a}_y,\mb{a}_z\) をそれぞれ \(x,y,z\) 軸の方向の単位ベクトルとすると, 電場 \(\mb{E}\) は
\begin{align*}
\mb{E}&=-\frac{1}{c}\ppdiff{\mb{A}}{t}-\nabla\phi \\
&=-\frac{e\mb{v}}{R^{*3}}\frac{v}{c^{2}}(x-vt) +\frac{e}{R^{*3}}
\left\{(x-vt)\mb{a}_x +\left(1-\frac{v^{2}}{c^{2}}\right)(y\mb{a}_y+z\mb{a}_z)\right\}\\
&=-\frac{e}{R^{*3}}\frac{v^{2}}{c^{2}}\mb{a}_x(x-vt)
+\frac{e}{R^{*3}}\left\{(x-vt)\mb{a}_x +\left(1-\frac{v^{2}}{c^{2}}\right)(y\mb{a}_y+z\mb{a}_z)\right\}\\
&=\frac{e}{R^{*3}}\left\{\left(1-\frac{v^{2}}{c^{2}}\right)(x-vt)\mb{a}_x
+\left(1-\frac{v^{2}}{c^{2}}\right)(y\mb{a}_y+z\mb{a}_z)\right\}\\
&=\frac{e}{R^{*3}}\left(1-\frac{v^{2}}{c^{2}}\right)
\bigl\{(x-vt)\mb{a}_x+y\mb{a}_y+z\mb{a}_z\bigr\}
\tag{*}
\end{align*}
このとき, 図 1. から,
\begin{align*}
&X=v(t_0-t)=vt_0-vt=x-vt,\\
&R=\sqrt{X^{2}+b^{2}}=\sqrt{(x-vt)^{2}+y^{2}+z^{2}}\quad\rightarrow\quad
\mb{R}=(x-vt)\mb{a}_x +y\mb{a}_y +z\mb{a}_z
\end{align*}
従って, 上式 (*) は次のように表せる:
\mb{E}=\frac{e}{R^{*3}}\left(1-\frac{v^{2}}{c^{2}}\right)\mb{R}
=\frac{e\mb{R}}{R^{*3}}\left(1-\frac{v^{2}}{c^{2}}\right)
\tag{11.6}
\end{equation}
次に磁場 \(\mb{H}\) を求める.\(\displaystyle \frac{1}{c}\ppdiff{\mb{A}}{t}=\frac{e\mb{v}}{R^{*3}}\frac{v}{c^{2}}(x-vt)\equiv f(x)\mb{v}\) と \(\mb{v}\) とが平行であることから,
\begin{align*}
\mb{E}=-f(x)\mb{v}-\nabla\phi\quad\rightarrow\quad
\mb{v}\times\mb{E}=\cancel{-f(x)\mb{v}\times\mb{v}}-\mb{v}\times\nabla\phi
=-\mb{v}\times\nabla\phi=-\mb{v}\times\nabla \left(\frac{e}{R^{*}}\right)
\end{align*}
従って, 磁場\(\mb{H}\) は上式の関係と「一様な運動を仮定しているから \(\mb{v}/c\) は一定である」ことを用いて次となる:
\begin{align*}
\mb{H}&=\mathrm{rot}\ \mb{A}
=\nabla\times \left(\frac{e}{R^{*}}\frac{\mb{v}}{c}\right)
=\nabla\left(\frac{e}{R^{*}}\right)\times\frac{\mb{v}}{c}
+\cancel{\left(\frac{e}{R^{*}}\right)\nabla\times \left(\frac{\mb{v}}{c}\right)}
=-\frac{\mb{v}}{c}\times \nabla\left(\frac{e}{R^{*}}\right)\\
&=\frac{1}{c}\left\{-\mb{v}\times\nabla\left(\frac{e}{R^{*}}\right)\right\}
=\frac{1}{c}\mb{v}\times\mb{E},\\
\therefore&\quad {\color{blue}\mb{H}=\frac{1}{c}\mb{v}\times\mb{E}}
\tag{11.7}
\end{align*}
これらの式から,「輻射は遅延の位置から放出されるのであるが, 干渉のために, ある時刻の電気力線はその同時時刻に於ける電荷の位置から引かれた直線 \(\mb{R}\) の方向を向いていること」が分かる.また, 場は電荷が静止いている場合の様に球対称にはならず, 進行方向よりもそれに垂直な方向に強くなっていることも分かる.言い換えれば, 法線は極方向に於けるよりも赤道面に於ける方が密になっている.すなわち, 赤道面では
|\mb{E}_{\mathrm{equ}}|=\frac{e}{\sqrt{\ds{1-\frac{v^{2}}{c^{2}}(y^{2}+z^{2})}}}
\end{equation*}
であり, 極方向では
|\mb{E}_{\mathrm{pol}}|=\frac{e}{(x-vt)^{2}}\left(1-\frac{v^{2}}{c^{2}}\right)
\end{equation*}
である.従って, 電荷の速度が光の速度 \(c\) に非常に近いようなときには, 電場の大部分は赤道面内に存在することになり, 3個のベクトル \(\mb{E},\mb{H},\mb{v}\) は互いに垂直であるから, 電荷が近くを通り過ぎたときの影響は実際には輻射による衝撃と同じ様な効果になる.
〜〜以下は略す.〜〜
References
| ↑1 | [ブログ註] この文章とほぼ同じものが, 砂川重信:「理論電磁気学」の第9章§3に例題として書かれているので, 参照することをお勧めする. |
|---|---|
| ↑2 | [ブログ註] この解の式を近似し, 分母の \(v^{2}\) と分子の根号内の \((c^{2}-v^{2})b^{2}\) を微小として省略するなどすると, \begin{equation*} t’ \sim \frac{c^{2}t-v^{2}t_0\pm cv(t_0-t)}{c^{2}}=t-\beta^{2} t_0 \pm \beta(t_0-t) \sim t\pm \beta(t_0-t) \end{equation*} となるが, 正号を取ると \(t’=t+\beta(t_0-t)>t\) となって, \(t'<t\) の仮定に反してしまうからである. |