\(\)
特殊相対論のローレンツ変換の公式を考える場合, 初等的教科書のほとんどは, 二つの座標系 \(K\) 及び \(K’\) は座標軸が平行で, 例えば \(K’\) 系が \(K\) 系に対して \(z\) 軸の正の方向に速度 \(v\) で運動している特別な場合が多い．しかし \(K’\) 系が \(K\) 系に対して「任意の速度 \(\mathbf{v}\) で平行移動している場合」の変換式はどうなるのであろうか？ その答えは, 例えば D. Jackson : 「電磁気学」の§ 11.2 や, Misner, Thorne, Wheeler : 「Gravitation」 の § 2. 10 の練習問題に提示されている．それらの記述を示しておこう．
次は Misner el al. : Gravitation § 2.10 の練習問題 2.7 の抜粋である：
Exercise 2.7 BOOST IN AN ARBITRARY DIRECTION
An especially useful Lorentz transformation \(x^{\mu’}=\Lambda^{\mu’}_{\ \nu}x^{\nu}\) has the matrix components
\begin{align}
\Lambda^{0′}_{\ 0} &= \gamma \equiv \frac{1}{\sqrt{1-\beta^{2}}},\\
\Lambda^{0′}_{\ j} &= \Lambda^{j’}_{\ 0} = -\beta\gamma n^{j},\\
\Lambda^{j’}_{\ k} &= \Lambda^{k’}_{\ j} = (\gamma -1)n^{j}n^{k} + \delta^{j k},\tag{2.44}\\
\Lambda^{\mu}_{\ \nu’}&= (\text{same as}\ \Lambda^{\nu’}_{\ \mu} \ \text{but with}\ \beta\ \text{replaced by}\ -\beta ),
\end{align}
where \(\beta,\,n^{1},\,n^{2}\) and \(n^{3}\) are parameters, and \(\def\mb#1{\mathbf{#1}}\mb{n}^{2}\equiv\big(n^{1}\big)^{2}+\big(n^{2}\big)^{2}+\big(n^{3}\big)^{2}=1\).
\begin{equation}
\Lambda^{\mu’}_{\ \nu}=\left( \begin{array}{@{\,}cccc@{\,}}
\gamma & -\beta\gamma n^{1} & -\beta\gamma n^{2} & -\beta\gamma n^{3} \\
-\beta\gamma n^{1} & (\gamma-1)n^{1}n^{1}+1 & (\gamma-1)n^{1}n^{2} & (\gamma-1)n^{1}n^{3}\\
-\beta\gamma n^{2} & (\gamma-1)n^{2}n^{1} & (\gamma-1)n^{2}n^{2}+1 & (\gamma-1)n^{2}n^{3}\\
-\beta\gamma n^{3} & (\gamma-1)n^{3}n^{1} & (\gamma-1)n^{3}n^{2}+1 & (\gamma-1)n^{3}n^{3}+1
\end{array}\right)
\end{equation}
そして, 以下は D. Jackson : 「電磁気学」の§ 11.2 の記述を補足したものである：
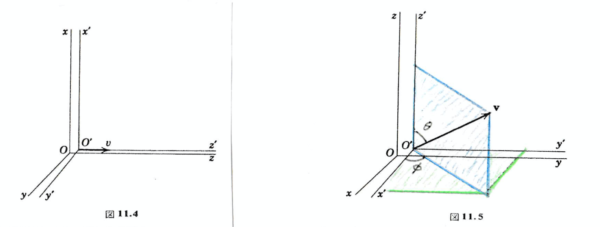
２つの座標系 \(K\) 及び \(K’\) を考える．\(K’\) 系の座標軸は \(K\) 系の座標軸に平行であるとする． 先ずは, \(K’\) 系が \(K\) 系に対して \(z\) 軸の正の方向に速度 \(v\) で運動しているとする．(図1の左図を参照)．
図 1.
このときの\(K\) 系の座標と \(K’\) 系の座標とを結び付ける Lorentz 変換は, 初等的な教科書で次のように記されているであろう：
\begin{align}
z’&=\gamma \big(z-v t\big),\quad \text{where}\quad \gamma=\frac{1}{\sqrt{1-\beta^{2}}},\ \beta=\frac{v}{c},\\
x’&=x,\quad y’=y\\
t’&=\gamma \left(t-\frac{v}{c^{2}}z\right)
\tag{1}
\end{align}
z’&=\gamma \big(z-v t\big),\quad \text{where}\quad \gamma=\frac{1}{\sqrt{1-\beta^{2}}},\ \beta=\frac{v}{c},\\
x’&=x,\quad y’=y\\
t’&=\gamma \left(t-\frac{v}{c^{2}}z\right)
\tag{1}
\end{align}
この式 (1) の変換は, \(K\) 系と \(K’\) 系の相対運動が \(z\) 軸に平行である特別な場合を表わしている．
それに対して図1の右図のように, \(K’\) 系が \(K\) 系に対して任意の速度 \(\mathbf{v}\) で平行移動している場合の変換式を考えてみる．式 (1) は明らかに座標ベクトルの \(\mb{v}\) に平行な成分 \(\mb{x}_{\parallel}=z\) と垂直な成分 \(\mb{x}_{\perp}=x,y\) に対して適用できることに注意する．従って, 式 (1) に於いて \(z\to \mb{x}_{\parallel}\) そして, \(x,y\to \mb{x}_{\perp}\) とすれば次が得られる：
\begin{align}
\mb{x}’_{\parallel}&=\gamma\big(\mb{x}_{\parallel}-\mb{v}t\big),\quad \mb{x}’_{\perp}=\mb{x}_{\perp},\\
t’&=\gamma\left(t-\frac{\mb{v}\cdot\mb{x}_{\parallel}}{c^{2}}\right)=\gamma\left(t-\frac{\mb{v}\cdot\mb{x}}{c^{2}}\right),\quad \gamma=\frac{1}{\sqrt{1-\beta^{2}}}
\tag{2}
\end{align}
\mb{x}’_{\parallel}&=\gamma\big(\mb{x}_{\parallel}-\mb{v}t\big),\quad \mb{x}’_{\perp}=\mb{x}_{\perp},\\
t’&=\gamma\left(t-\frac{\mb{v}\cdot\mb{x}_{\parallel}}{c^{2}}\right)=\gamma\left(t-\frac{\mb{v}\cdot\mb{x}}{c^{2}}\right),\quad \gamma=\frac{1}{\sqrt{1-\beta^{2}}}
\tag{2}
\end{align}
ただし, \(\mb{n}\) を ベクトル \(\mb{v}\) 方向の単位ベクトル即ち \(\mb{v}=v\mb{n}\) とし, また明らかに \(\mb{x}=\mb{x}_{\parallel}+\mb{x}_{\perp}\) なので, 次式が言えることに注意する：
\begin{align}
&v z\to \mb{v}\cdot\mb{x}_{\parallel}=\mb{v}\cdot\left(\mb{x}_{\parallel}+\mb{x}_{\perp}\right)=\mb{v}\cdot\mb{x},
\quad \text{because}\quad \mb{x}=\mb{x}_{\perp}+\mb{x}_{\parallel},\quad \mb{v}\cdot\mb{x}_{\perp}=0\\
&\frac{\mb{v}}{v^{2}}(\mb{v}\cdot\mb{x})=\frac{\mb{v}}{v^{2}}(\mb{v}\cdot\mb{x}_{\parallel})=\mb{n}(\mb{n}\cdot\mb{x}_{\parallel})=\mb{n}|\mb{x}_{\parallel}|=\mb{x}_{\parallel},\quad \text{therfore}\quad \mb{x}_{\parallel}=\frac{(\mb{v}\cdot\mb{x})\mb{v}}{v^{2}}
\tag{3}
\end{align}
&v z\to \mb{v}\cdot\mb{x}_{\parallel}=\mb{v}\cdot\left(\mb{x}_{\parallel}+\mb{x}_{\perp}\right)=\mb{v}\cdot\mb{x},
\quad \text{because}\quad \mb{x}=\mb{x}_{\perp}+\mb{x}_{\parallel},\quad \mb{v}\cdot\mb{x}_{\perp}=0\\
&\frac{\mb{v}}{v^{2}}(\mb{v}\cdot\mb{x})=\frac{\mb{v}}{v^{2}}(\mb{v}\cdot\mb{x}_{\parallel})=\mb{n}(\mb{n}\cdot\mb{x}_{\parallel})=\mb{n}|\mb{x}_{\parallel}|=\mb{x}_{\parallel},\quad \text{therfore}\quad \mb{x}_{\parallel}=\frac{(\mb{v}\cdot\mb{x})\mb{v}}{v^{2}}
\tag{3}
\end{align}
よって, 上式 (2) から次のような「同次の一般的な Lorentz 変換式」が得られる：
\begin{align}
\mb{x}’&=\mb{x}+(\gamma-1)\frac{\mb{v}\cdot\mb{x}}{v^{2}}\mb{v}-\gamma\mb{v}t,\\
t’&=\gamma\left(t-\frac{\mb{v}\cdot\mb{x}}{c^{2}}\right)\quad\text{or,}\quad
c t’=\gamma\left(c t-\frac{\mb{v}\cdot\mb{x}}{c}\right)
\tag{4}
\end{align}
\mb{x}’&=\mb{x}+(\gamma-1)\frac{\mb{v}\cdot\mb{x}}{v^{2}}\mb{v}-\gamma\mb{v}t,\\
t’&=\gamma\left(t-\frac{\mb{v}\cdot\mb{x}}{c^{2}}\right)\quad\text{or,}\quad
c t’=\gamma\left(c t-\frac{\mb{v}\cdot\mb{x}}{c}\right)
\tag{4}
\end{align}
\(\displaystyle{n^{i}=\frac{v^{i}}{v}}\) として, これを座標成分で表現し直すと,
\begin{align}
x’^{j}&=x^{j}+(\gamma-1)\left(x^{1}\frac{v_1}{v}+x^{2}\frac{v_2}{v}+x^{3}\frac{v_3}{v}\right)\frac{v^{j}}{v}
-\gamma\frac{v^{j}}{v}\frac{v}{c}c t\\
&=\delta^{j}_{\ k}x^{k}+(\gamma-1)x^{k}n^{k}n^{j}-\beta\gamma n^{j} c t\\
&= -\beta\gamma n^{j} c t+\left\{\delta^{j}_{\ k}+(\gamma-1) n^{k} n^{j}\right\}x^{k}\\
ct’ &=\gamma c t-\gamma\frac{\mb{x}\cdot\mb{v}}{c}=\gamma c t -\gamma \frac{v}{c}\left(\frac{v_x}{v}x+\frac{v_y}{v}y+\frac{v_z}{v}z\right)\\
&=\gamma c t -\gamma\beta n^{1}x^{1}-\gamma\beta n^{2}x^{2}-\gamma\beta n^{3} x^{3}\\
&=\gamma c t -\beta\gamma n^{k}x^{k}
\tag{5}
\end{align}
x’^{j}&=x^{j}+(\gamma-1)\left(x^{1}\frac{v_1}{v}+x^{2}\frac{v_2}{v}+x^{3}\frac{v_3}{v}\right)\frac{v^{j}}{v}
-\gamma\frac{v^{j}}{v}\frac{v}{c}c t\\
&=\delta^{j}_{\ k}x^{k}+(\gamma-1)x^{k}n^{k}n^{j}-\beta\gamma n^{j} c t\\
&= -\beta\gamma n^{j} c t+\left\{\delta^{j}_{\ k}+(\gamma-1) n^{k} n^{j}\right\}x^{k}\\
ct’ &=\gamma c t-\gamma\frac{\mb{x}\cdot\mb{v}}{c}=\gamma c t -\gamma \frac{v}{c}\left(\frac{v_x}{v}x+\frac{v_y}{v}y+\frac{v_z}{v}z\right)\\
&=\gamma c t -\gamma\beta n^{1}x^{1}-\gamma\beta n^{2}x^{2}-\gamma\beta n^{3} x^{3}\\
&=\gamma c t -\beta\gamma n^{k}x^{k}
\tag{5}
\end{align}
更に, 4次元座標 \(x^{\mu}\) で表現した「同次の一般的な Lorentz 変換式」 (非同次なローレンツ変換 \(\mb{x}^{\mu}=\Lambda^{\mu}_{\ \nu}x^{\nu}+a^{\mu}\) は「ポアンカレ変換」と呼ばれる) に書くならば,
\begin{align}
x’^{\mu} = \Lambda^{\mu}_{\ \nu}&x^{\nu},\\
x’^{j} &= \Lambda^{j}_{\ \nu}x^{\nu}=\Lambda^{j}_{\ 0} c t +\Lambda^{j}_{\ k} x^{k}\\
x’^{0} &= c t’=\Lambda^{0}_{\ \nu}x^{\nu}=\Lambda^{0}_{\ 0}c t +\Lambda^{0}_{\ k}x^{k}
\tag{6}
\end{align}
x’^{\mu} = \Lambda^{\mu}_{\ \nu}&x^{\nu},\\
x’^{j} &= \Lambda^{j}_{\ \nu}x^{\nu}=\Lambda^{j}_{\ 0} c t +\Lambda^{j}_{\ k} x^{k}\\
x’^{0} &= c t’=\Lambda^{0}_{\ \nu}x^{\nu}=\Lambda^{0}_{\ 0}c t +\Lambda^{0}_{\ k}x^{k}
\tag{6}
\end{align}
式 (5) と式 (6) とを比較するならば, 式 (5) の結果は, 前述の Misner の式 (2.44) に一致することが分かる：
\begin{equation}
\Lambda^{j}_{\ 0}=-\beta\gamma n^{j},\quad \Lambda^{j}_{\ k}=\delta^{j}_{\ k}+(\gamma-1)n^{j}n^{k},\quad
\Lambda^{0}_{\ 0}=\gamma,\quad \Lambda^{0}_{\ k} = -\beta\gamma n^{k}
\tag{7}
\end{equation}
\Lambda^{j}_{\ 0}=-\beta\gamma n^{j},\quad \Lambda^{j}_{\ k}=\delta^{j}_{\ k}+(\gamma-1)n^{j}n^{k},\quad
\Lambda^{0}_{\ 0}=\gamma,\quad \Lambda^{0}_{\ k} = -\beta\gamma n^{k}
\tag{7}
\end{equation}
( 参考 ) 内山：「相対性理論」によれば, 「一般の Lorentz 変換」は次のように定義される：
任意の世界点 \(P\) の \(S\), \(S’\) から見た座標をそれぞれ \(x^{\mu}\), \(x’^{\mu}\) とする．いま \(x^{\mu}\) と \(x’^{\mu}\) の間に
\begin{equation}
x’^{\mu}=\Lambda^{\mu}_{\ \nu} x^{\nu} + b^{\mu}
\tag{8}
\end{equation}
の関係があるとする． 更に, 光速度不変の原理に基づく次の条件を満たすとする：
\begin{equation}
s^{2}\equiv \eta_{\mu\nu}x^{\mu}x^{\nu}=\eta_{\mu\nu}x’^{\mu}x’^{\nu}
\tag{9}
\end{equation}
ただし, \(\eta_{\mu\nu}\) は「平坦時空の計量テンソル」で, その符号系は Misner 本と同じ \((-+++)\)とする．
このとき, 変換 \(x^{\mu}\to x’^{\mu}\) は「Lorentz 変換」である．式 (9) を式 (8) に代入して \(x\) の係数を比較すると次式が成り立つ：
\begin{equation}
\eta_{\mu\nu}=\eta_{\rho\sigma}\Lambda^{\rho}_{\ \mu}\Lambda^{\sigma}_{\ \nu}=\Lambda^{\rho}_{\ \mu} \eta_{\rho\sigma} \Lambda^{\sigma}_{\ \nu}
\tag{10}
\end{equation}
従って, 「式 (8) で定義された座標変換 \(x^{\mu}\to x’^{\mu}\) に於いて,その係数 \(\Lambda^{\mu}_{\ \nu}\) が式 (10) を満たすとき, それは Lorentz 変換である」．
この式 (10) を, 「\(\Lambda^{\mu}_{\ \nu}\) を行列要素とする \(4\times 4\)行列 \(\mb{\Lambda}\)」と 「\(\eta_{\mu\nu}\) を行列要素とする \(4\times 4\)行列 \(\mb{\eta}\)」 とで表現してみる．「\(\mb{\Lambda}\) の転置行列を \(\mb{\Lambda}^{T}\)」 と記すならば,
\begin{equation}
\big(\mb{\Lambda}\big)_{\mu\nu}\equiv \Lambda^{\mu}_{\ \nu},\quad\rightarrow\quad
\big(\mb{\Lambda}^{T}\big)_{\mu\nu}\equiv \big(\mb{\Lambda}\big)_{\nu\mu}=\Lambda^{\nu}_{\ \mu},\quad \text{and}\quad
\big(\mb{\eta}\big)_{\mu\nu}\equiv \eta_{\mu\nu}
\tag{11}
\end{equation}
\big(\mb{\Lambda}\big)_{\mu\nu}\equiv \Lambda^{\mu}_{\ \nu},\quad\rightarrow\quad
\big(\mb{\Lambda}^{T}\big)_{\mu\nu}\equiv \big(\mb{\Lambda}\big)_{\nu\mu}=\Lambda^{\nu}_{\ \mu},\quad \text{and}\quad
\big(\mb{\eta}\big)_{\mu\nu}\equiv \eta_{\mu\nu}
\tag{11}
\end{equation}
となるから, 式 (10) の行列表現は次となる：
\begin{equation}
\eta_{\mu\nu}=\Lambda^{\rho}_{\ \mu} \eta_{\rho\sigma} \Lambda^{\sigma}_{\ \nu}=\big(\mb{\Lambda}^{T}\big)_{\mu\rho}
\big(\mb{\eta}\big)_{\rho\sigma}\big(\mb{\Lambda}\big)_{\sigma\nu}
\quad\rightarrow\quad
\big(\mb{\eta}\big)_{\mu\nu}=\big(\mb{\Lambda}^{T}\mb{\eta}\mb{\Lambda}\big)_{\mu\nu}
\tag{12}
\end{equation}
\eta_{\mu\nu}=\Lambda^{\rho}_{\ \mu} \eta_{\rho\sigma} \Lambda^{\sigma}_{\ \nu}=\big(\mb{\Lambda}^{T}\big)_{\mu\rho}
\big(\mb{\eta}\big)_{\rho\sigma}\big(\mb{\Lambda}\big)_{\sigma\nu}
\quad\rightarrow\quad
\big(\mb{\eta}\big)_{\mu\nu}=\big(\mb{\Lambda}^{T}\mb{\eta}\mb{\Lambda}\big)_{\mu\nu}
\tag{12}
\end{equation}
式 (7) すなわち式 (2.44) の \(\Lambda^{\mu}_{\ \nu}\) が, 上式 (12) を満足することは実際に行列計算をして確かめることが出来る．例えば, Maxima を用いた結果は次となった：
図 2.最後の結果は, 条件式 \(\mb{n}^{2}=(n^{1})^{2}+(n^{1})^{2}+(n^{1})^{2}=1\) を用いることで \(L=\eta_{\mu\nu}\) に一致することが分かる．
また, 式 (2.44) を回転行列を用いて求める方法もあるらしい．例えば, 次のサイトの文章に分かり易い導出の説明が示されていた：
https://www.phyas.aichi-edu.ac.jp/~takahasi/Project_H_pdf/Rel.SgrA.2.pdf
その文中の 5.6 ローレンツ変換の一般的表現(任意の向きの相対速度) に於ける 次の式
\begin{equation}
L_{gen}(\vec{v}) = \mathcal{R}^{-1}(\theta,\phi)\,L_x(\vec{v})\,\mathcal{R}(\theta,\phi)
\tag{5.10}
\end{equation}
L_{gen}(\vec{v}) = \mathcal{R}^{-1}(\theta,\phi)\,L_x(\vec{v})\,\mathcal{R}(\theta,\phi)
\tag{5.10}
\end{equation}
の具体的な計算を, やはり Maxima で実行して見たので, その結果を示しておこう：
図 3.
ここでは, 前述の\(n^{i}\) は「方向余弦である」と考えて, それを図 1. のような3次元極座標の角度で表した次の関係式
\begin{align}
n^{1}&=\frac{v_x}{v}=\cos\alpha=\sin\theta\cos\phi,\\
n^{2}&=\frac{v_y}{v}=\cos\beta=\sin\theta\sin\phi,\\
n^{3}&=\frac{v_z}{v}=\cos\gamma=\cos\theta
\tag{13}
\end{align}
n^{1}&=\frac{v_x}{v}=\cos\alpha=\sin\theta\cos\phi,\\
n^{2}&=\frac{v_y}{v}=\cos\beta=\sin\theta\sin\phi,\\
n^{3}&=\frac{v_z}{v}=\cos\gamma=\cos\theta
\tag{13}
\end{align}
を用いて表している． この関係式 (13) および三角関数の公式を図 3. 中の最後の結果式に当てはめるならば, ちょうど式 (2.44) に一致する結果になっていることが確かめられると思う．
