反変ベクトルと共変ベクトルの違いの図示


多くの教科書で,『4元ベクトルには共変成分と反変成分の2種類がある』と習う．例えば, ランダウ：「力学・場の理論」§ 38 では次のようである：

全ての4元ベクトル $A^{\mu}$ の大きさの2乗 $A^2$ は, 動径4元ベクトル $x^{\mu}$ の2乗 $x^2$ と同様に次で定義される：

\begin{equation}
x^2=(x^0)^2 -(x^1)^2 -(x^2)^2 -(x^3)^2,\quad\rightarrow\quad
A^2=(A^0)^2 -(A^1)^2 -(A^2)^2 -(A^3)^2
\end{equation}

この種の表式を書くのに便利なように, 4元ベクトルの「2種類」の成分を導入し, 添字を上あるいは下側に付けた記号 $A^{\mu}$ 及び $A_{\mu}$ でそれらを表そう．そうして

\begin{equation}
A_0=A^{0},\quad A_1=-A^{1},\quad A_2=-A^{2},\quad A_3=-A^{3}
\tag{38.2}
\end{equation}

とする．量 $A^{\mu}$ は4元ベクトルの「反変成分」, $A_{\mu}$ は「共変成分」と呼ばれる．

しかし「この2種類の成分はどのように違うのか」を直観的に理解することは難しいであろう．その違いを斜交座標の場合に図示した説明が, 例えば高橋康：「場の解析力学入門」や藤井保憲：「時空と重力」に載っている．ここでは藤井の§ 11 の説明を取り上げる．ただし, その文章は斜交座標が直交座標に対して $45$°の場合である．その角度を一般化してもほとんど同じ筋で行けるので, そのように修正した説明を示しておく．

斜交座標

線素と計量テンソル

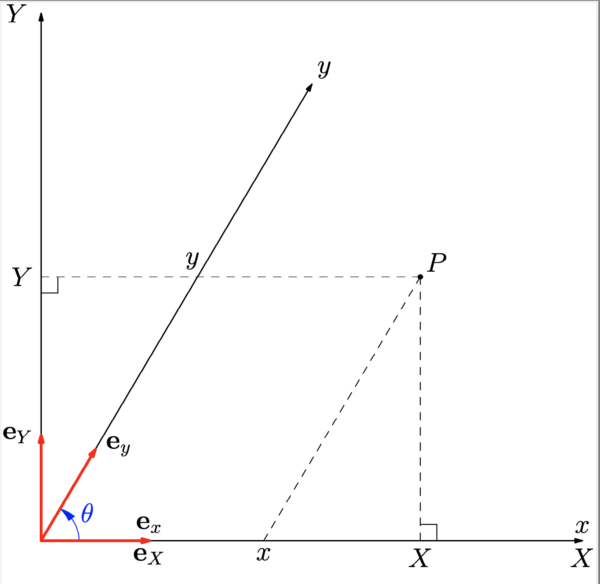
直交座標でない座標系の中で最も簡単なものは「斜交座標」である．例えば2次元の直交座標 $X=X^{1}$, $Y=X^{2}$ に対して角度 $\theta$ の線を $y$ 軸に選び, $x$ 軸は元の $X$ 軸に一致させておく．図 1 から分かるように同じ点 $P$ の座標に対して次が成り立つ：

\begin{equation}
\def\mb#1{\mathbf{#1}}
\def\mr#1{\mathrm{#1}}
\def\reverse#1{\frac{1}{#1}}
\def\ds#1{\mbox{${\displaystyle\strut #1}$}}
\begin{cases} \ds{x^1 = x = X-\frac{Y}{\tan \theta}},\\ \ds{x^2=y=\frac{Y}{\sin\theta}}\end{cases}\quad\longleftrightarrow
\quad \begin{cases} X=x+y\cos\theta\\ Y=y\sin\theta \end{cases}
\tag{11-1,2}
\end{equation}

直交座標系の $X,\,Y$ 軸方向の「単位ベクトル」$\mb{e}_X,\mb{e}_Y$ と, 斜交座標系の $x,y$ 軸方向の「単位ベクトル」$\mb{e}_x,\mb{e}_y$ を導入する．それらの成分は次となる：

\begin{equation}
\mb{e}_X=(1,0),\quad \mb{e}_Y=(0,1),\quad
\mb{e}_x=(1,0),\quad \mb{e}_y=(\cos\theta,\sin\theta)
\tag{11-3,4}
\end{equation}

このとき $\mb{e}_x,\mb{e}_y$ はそれぞれ規格化されているが, 互いに直交ではない．実際,

\begin{equation}
\mb{e}_x \cdot \mb{e}_y = (1,0)\cdot(\cos\theta,\sin\theta)
=1\times\cos\theta+0\times\sin\theta=\cos\theta \ne 0
\tag{11-5}
\end{equation}

図 1. 2次元の斜交座標と単位ベクトルの組．

次に無限小線素を考える．座標 $X,\,Y$ を持つ点 $P$ に非常に近い点 $Q$ をとり, その座標を $X+dX$, $Y+dY$ とする．$PQ$ 間の距離 $ds$ は,

\begin{equation}
(ds)^2 = (dX)^2 + (dY)^2
\tag{11-6}
\end{equation}

で与えられるが, これを斜交座標で表わしてみる．点 $P$ の斜交座標を $x,y$ とし, 点 $Q$ のそれを $x+dx$, $y+dy$ とすると, 式 (11-1,2) から

\begin{equation}
dX = dx +\cos\theta\,dy,\quad dY=\sin\theta\,dy
\tag{11-7}
\end{equation}

となるので, これを上式 (11-6) に代入すると

\begin{align}
(ds)^2 &= \bigl(dx +\cos\theta\,dy\bigr)^2 + \bigl(\sin\theta\,dy\bigr)^2\notag\\
&=(dx)^2 +\cos\theta\,dx\,dy +\cos\theta\,dy\,dx + \sin^2\theta\,(dy)^2\notag\\
&\equiv g_{xx}\,(dx)^2 + g_{xy}\,dx\,dy + g_{yx}\,dy\,dx + g_{yy}\,(dy)^2\notag\\
&\equiv g_{11}\,(dx)^2 + g_{12}\,dx\,dy + g_{21}\,dy\,dx + g_{22}\,(dy)^2
\tag{11-8}
\end{align}

上式の各項の係数 $g_{\mu\nu}$ は「計量テンソル」または単に「計量」と呼ばれる．それを成分とする行列 $\mb{g}=(g_{\mu\nu})$ は, この場合「対称行列」になる：

\begin{equation}
g_{\mu\nu}=\begin{pmatrix} g_{11} & g_{12} \\ g_{21} & g_{22} \end{pmatrix}
=\begin{pmatrix}
1 & \cos\theta \\ \cos\theta & 1
\end{pmatrix}
\tag{11-12}
\end{equation}

直交座標系の場合の計量を特にバーを付けて書くことにすると, それは「単位行列」$\mb{1}$ となることは明らかである：

\begin{equation}
\bar{g}_{\mu\nu}=\begin{pmatrix}
1 & 0 \\ 0 & 1
\end{pmatrix}
=\delta_{\mu\nu}
\tag{11-14}
\end{equation}

ただし $\delta_{\mu\nu}$ は「Kronecker のデルタ記号」である．また次式が成り立つことが言える：

\begin{equation}
\mb{e}_{\mu}\cdot\mb{e}_{\nu}=\delta_{\mu\nu}
\tag{11-15}
\end{equation}

これは一般の斜交座標でも成り立つ重要な関係式である．

ベクトルの成分

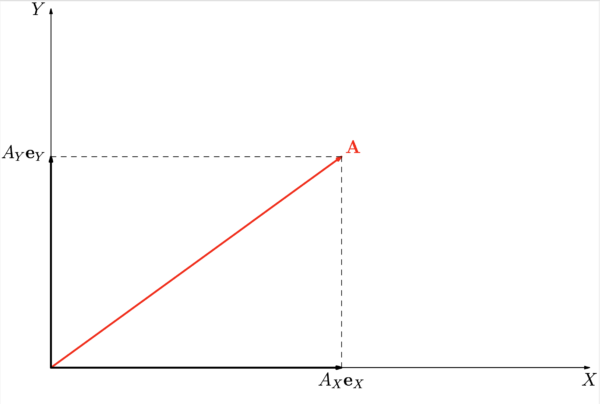
直交座標系では, ベクトル $\mb{A}$ とその成分は, 単位ベクトル $\mb{e}_{X}$, $\mb{e}_{Y}$ を用いて次のように表わされる(図2を参照)：

\begin{equation}
\mb{A}=A_{X}\mb{e}_{X} + A_{Y}\mb{e}_{Y},\quad\mathrm{where}\quad
A_{X}=\mb{A}\cdot\mb{e}_{X},\quad A_{Y}=\mb{A}\cdot\mb{e}_{Y}
\tag{11-16,17}
\end{equation}

図 2. 直交座標に於けるベクトルの成分．

同じことが斜交座標系でも成り立つであろうか？．上式に倣って成分を次式によって定義してみる：

\begin{equation}
A_x=\mb{A}\cdot{e}_{x},\quad A_{y}=\mb{A}\cdot\mb{e}_{y}
\tag{11-18}
\end{equation}

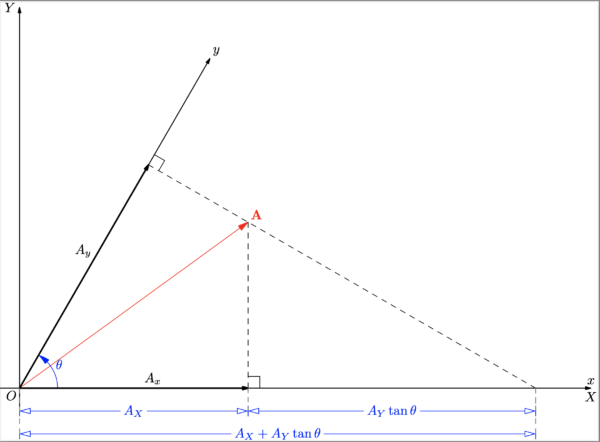
その幾何学的な意味は, 下図 3 から明らかであろう．

図 3. 斜交座標に於けるベクトルの共変成分．

そこで前式 (11-17) を上式 (11-18) に代入してみると

\begin{align}
A_x&=(A_{X}\mb{e}_{X} + A_{Y}\mb{e}_{Y})\cdot\mb{e}_{x}
=A_{X}\,(\mb{e}_{X}\cdot\mb{e}_{x})+A_{Y}\,(\mb{e}_{Y}\cdot\mb{e}_{x}),\notag\\
A_{y}&=(A_{X}\mb{e}_{X} + A_{Y}\mb{e}_{Y})\cdot\mb{e}_{y}
=A_{X}\,(\mb{e}_{X}\cdot\mb{e}_{y})+A_{Y}\,(\mb{e}_{Y}\cdot\mb{e}_{y})
\tag{11-19}
\end{align}

このとき式 (11-3,4) から

\begin{equation}
(\mb{e}_{X}\cdot\mb{e}_{x})=1,\quad (\mb{e}_{Y}\cdot\mb{e}_{x})=0,
\quad (\mb{e}_{X}\cdot\mb{e}_{y})=\cos\theta,
\quad (\mb{e}_{Y}\cdot\mb{e}_{y})=\sin\theta
\tag{11-20}
\end{equation}

これを前式 (11-19) に代入すると,

\begin{equation}
A_x=A_{X},\qquad
A_y=A_{X}\cos\theta +A_{Y}\sin\theta =\cos\theta\bigl(A_{X}+A_{Y}\tan\theta\bigr)
\tag{11-21}
\end{equation}

この関係式の幾何学的意味も図 3 に示してある．ところが, このような成分 $A_x,A_y$ を使って式 (11-17) のように $A_x\mb{e}_x+A_y\mb{e}_y$ を作っても $\mb{A}$ にはならないことは,やはり図 3 から直ぐ分かる．では斜交座標系でも, 式 (11-17) のような式が成り立つようなベクトル成分は存在するのであろうか？実はそのような成分は, 以下のようにして作ることが可能である．

まず式 (11-12) の計量テンソル $\mb{g}=g_{\mu\nu}$ の「逆行列」$\mb{g}^{-1}$ を作り, それを $g^{\mu\nu}$ と書くことにする．逆行列という意味は $g^{\nu\lambda}$ が次を満たすということである：

\begin{equation}
\mb{g}\,\mb{g}^{-1}=\mb{1}\quad\longleftrightarrow\quad
g_{\mu\nu}\,g^{\nu\lambda}=\delta_{\mu}^{\ \lambda}
\tag{11-22}
\end{equation}

ただし $\delta_{\mu}^{\ \lambda}$ はやはり Kronecker のデルタ記号である．$g^{\mu\nu}$ は行列 $\mb{g}$ の逆行列である．従って逆行列を求める公式から, 行列 $g_{\mu\nu}$ の「行列式」を $g=\mathrm{det}(g_{\mu\nu})$ として次となる：

\begin{equation}
g^{\mu\nu}=\frac{1}{g}\begin{pmatrix}
1 & -\cos\theta \\ -\cos\theta & 1
\end{pmatrix},
\qquad g=g_{11}g_{22}-g_{12}g_{21}=1-\cos^2\theta=\sin^2\theta
\tag{11-23}
\end{equation}

この $g^{\mu\nu}$ を用い, 式 (11-18) で定義した成分 $A_{\mu}$ から

\begin{equation}
A^{\mu}=g^{\mu\nu}\,A_{\nu}
\tag{11-27}
\end{equation}

という量を作ってみると,

\begin{equation*}
\begin{cases}
A^{x}=A^{1}=g^{11}A_1 + g^{12}A_2
=\ds{\frac{1}{\sin^{2}\theta}\bigl(A_x – A_y\cos\theta\bigr)},\\
A^{y}=A^{2}=g^{21}A_1 + g^{22}A_2
=\ds{\frac{1}{\sin^{2}\theta}\bigl(-A_{x}\cos\theta +A_{y}\bigr)}
\end{cases}
\end{equation*}

これに式 (11-21) の $A_x,A_y$ を用いると次となる：

\begin{equation}
\begin{cases}
A^{x}=\ds{A_X-\frac{A_Y}{\tan\theta}},\\
A^{y}=\ds{\frac{A_Y}{\sin\theta}}
\end{cases}
\tag{11-28}
\end{equation}

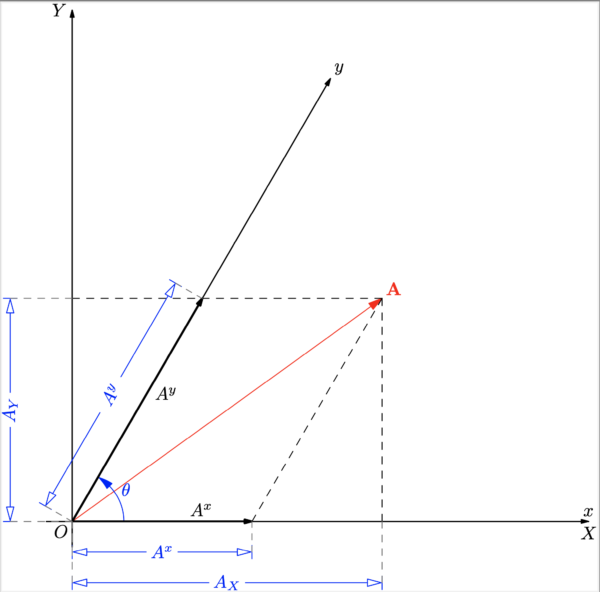
これの幾何学的な意味は図 4 に示しておく．今度は式 (11-17) と類似した関係式として

\begin{equation}
\mb{A}=A^{x}\mb{e}_x + A^{x}\mb{e}_y=A^{1}\mb{e}_1 + A^{2}\mb{e}_2=A^{\mu}\mb{e}_{\mu}
\tag{11-31}
\end{equation}

という型にまとめられる．