\(\)
第5章及び第6章の議論を理解するための数学的準備として, 有馬・神部:「複素関数論」の § 9.2 「積分の主値および佐藤の超関数」(p.109 \(\sim\)) からの抜粋を記しておく.
次の実軸上の積分 \(I\) の評価を考える.まず \(x\) を複素変数 \(z\) に置き換えて, 被積分関数を複素平面に解析接続した関数 \(F(z)\) を定義する:
\begin{equation}
I=\int_{-\infty}^{\infty} \frac{f(x)}{x-a}\,dx,\quad\rightarrow\quad
F(z)=\frac{f(z)}{z-a}
\tag{1}
\end{equation}
I=\int_{-\infty}^{\infty} \frac{f(x)}{x-a}\,dx,\quad\rightarrow\quad
F(z)=\frac{f(z)}{z-a}
\tag{1}
\end{equation}
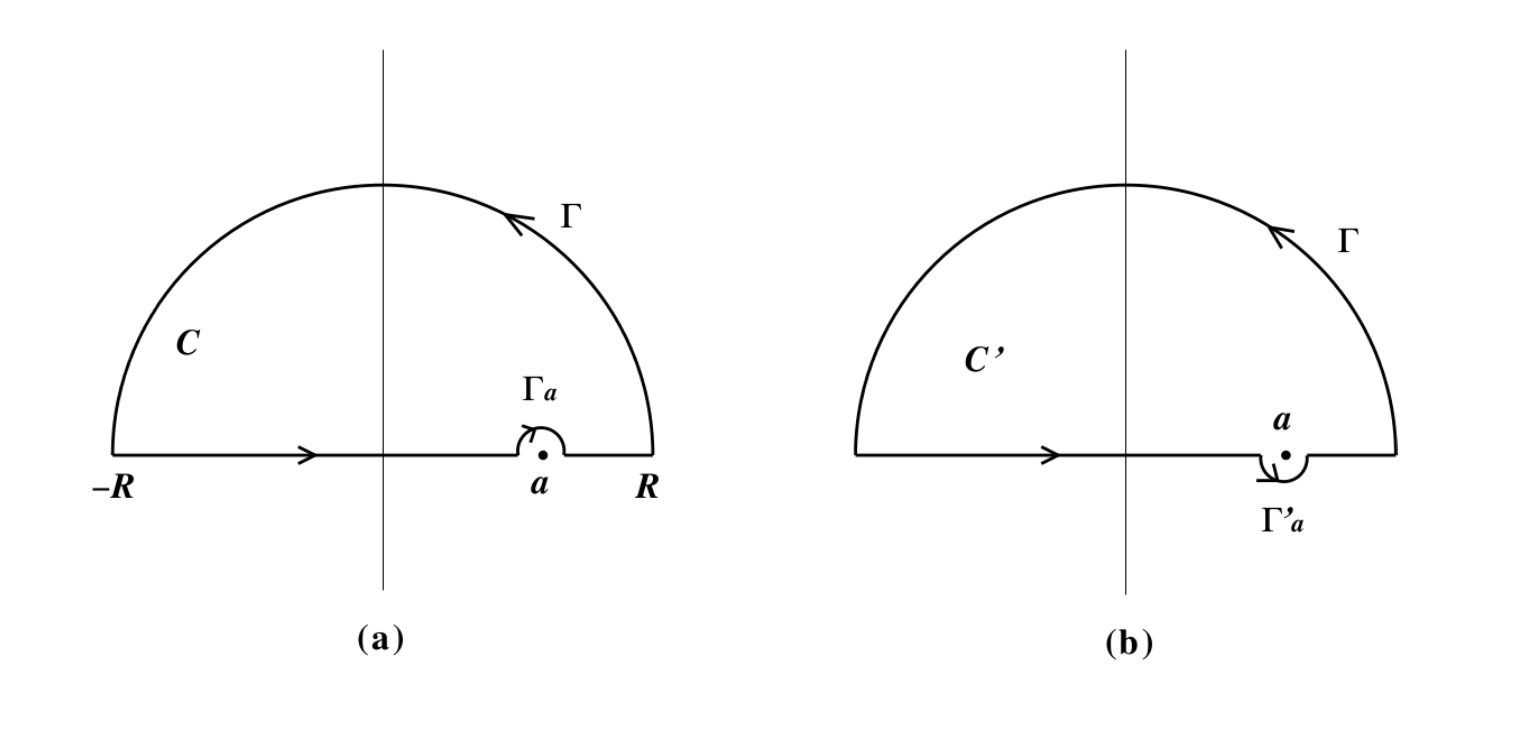
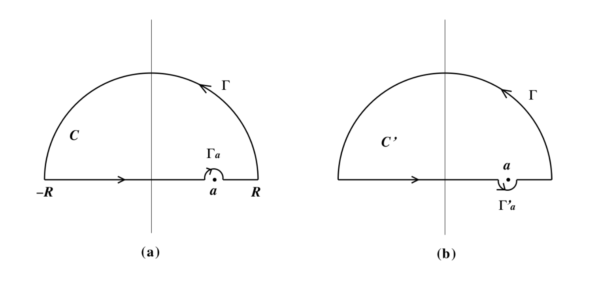
ただし, 分子の関数 \(f(z)\) は \(z=a\) のみならず実軸上で正則であるとし, また \(|z|^{k}|f(z)|\) は有界であるとする.関数 \(F(z)\) は点 \(a\) に一位の極を持っている.そこで下図 1. の (a)のような極 \(a\) の上方を迂回する実軸に沿う経路と十分大きな半径 \(R\) の上半面 \(\Gamma\) 上の閉曲線 \(C\) 上の積分を考える. \(a\) を迂回する曲線は半径 \(\varepsilon\) の半円 \(\Gamma_a\) とする.このとき,「留数の定理」より次が言える:
\begin{align}
\oint_{C} \frac{f(z)}{z-a}\,dz &= \int_{-R}^{a-\varepsilon}\frac{f(x)}{x-a}\,dx+
\int_{a+\varepsilon}^{R}\frac{f(x)}{x-a}\,dx+\int_{\Gamma_{a}}\frac{f(z)}{z-a}\,dz +\int_{\Gamma}\frac{f(z)}{z-a}\,dz\\
&=2\pi i\,[ C 内の極の留数の和 ]
\tag{2}
\end{align}
\oint_{C} \frac{f(z)}{z-a}\,dz &= \int_{-R}^{a-\varepsilon}\frac{f(x)}{x-a}\,dx+
\int_{a+\varepsilon}^{R}\frac{f(x)}{x-a}\,dx+\int_{\Gamma_{a}}\frac{f(z)}{z-a}\,dz +\int_{\Gamma}\frac{f(z)}{z-a}\,dz\\
&=2\pi i\,[ C 内の極の留数の和 ]
\tag{2}
\end{align}
このとき最後の項は \(R\to\infty\) のとき無限小となるので無視できる.また第3項は \(\varepsilon\to 0\) のとき \(z-a=\varepsilon e^{i\theta}\) とおくと \(dz=i\varepsilon e^{i\theta}d\theta\) なので次となる:
\begin{align}
\int_{\Gamma_a}\frac{f(z)}{z-a}\,dz
&=\int_{\pi}^{0}\frac{f(a+\varepsilon e^{i\theta})}{\varepsilon e^{i\theta}}i\,\varepsilon e^{i\theta}\,d\theta
=-i\int_{0}^{\pi}f(a+\varepsilon e^{i\theta})\,d\theta\\
&\xrightarrow{\varepsilon\to 0}\
-i\int_{0}^{\pi}f(a)\,d\theta=-if(a)\times \pi =-i\pi f(a)
\tag{3}
\end{align}
\int_{\Gamma_a}\frac{f(z)}{z-a}\,dz
&=\int_{\pi}^{0}\frac{f(a+\varepsilon e^{i\theta})}{\varepsilon e^{i\theta}}i\,\varepsilon e^{i\theta}\,d\theta
=-i\int_{0}^{\pi}f(a+\varepsilon e^{i\theta})\,d\theta\\
&\xrightarrow{\varepsilon\to 0}\
-i\int_{0}^{\pi}f(a)\,d\theta=-if(a)\times \pi =-i\pi f(a)
\tag{3}
\end{align}
ここで, 次の量を「コーシーの積分主値 (principal value)」と呼ぶ:
\begin{equation}
\mathrm{P}\int_{-\infty}^{\infty}\frac{f(x)}{x-a}\,dx
\equiv \lim_{\varepsilon\to+0}\left[\ \int_{-\infty}^{a-\varepsilon}\frac{f(x)}{x-a}\,dx
+\int_{a+\varepsilon}^{\infty}\frac{f(x)}{x-a}\,dx\ \right]
\tag{4}
\end{equation}
\mathrm{P}\int_{-\infty}^{\infty}\frac{f(x)}{x-a}\,dx
\equiv \lim_{\varepsilon\to+0}\left[\ \int_{-\infty}^{a-\varepsilon}\frac{f(x)}{x-a}\,dx
+\int_{a+\varepsilon}^{\infty}\frac{f(x)}{x-a}\,dx\ \right]
\tag{4}
\end{equation}
以上のことから, 式(2)は \(R\to\infty\), \(\varepsilon\to 0\) の極限で次に書けることが分かる:
\begin{equation}
\oint_{C} \frac{f(z)}{z-a}\,dz = \mathrm{P}\int_{-\infty}^{\infty}\frac{f(x)}{x-a}\,dx\,-i\pi\,f(a)
\tag{5}
\end{equation}
\oint_{C} \frac{f(z)}{z-a}\,dz = \mathrm{P}\int_{-\infty}^{\infty}\frac{f(x)}{x-a}\,dx\,-i\pi\,f(a)
\tag{5}
\end{equation}
次に, 点 \(a\) の迂回の仕方を変えて上図 1. の (b) のようにしてみる.今度の閉曲線 \(C’\) についての積分は, 式 (3) に対応する値は \(i\pi f(a)\) になるので次となる:
\begin{equation}
\oint_{C’} \frac{f(z)}{z-a}\,dz=\mathrm{P}\int_{-\infty}^{\infty}\frac{f(x)}{x-a}\,dx\,+i\pi\,f(a)
\tag{6}
\end{equation}
\oint_{C’} \frac{f(z)}{z-a}\,dz=\mathrm{P}\int_{-\infty}^{\infty}\frac{f(x)}{x-a}\,dx\,+i\pi\,f(a)
\tag{6}
\end{equation}
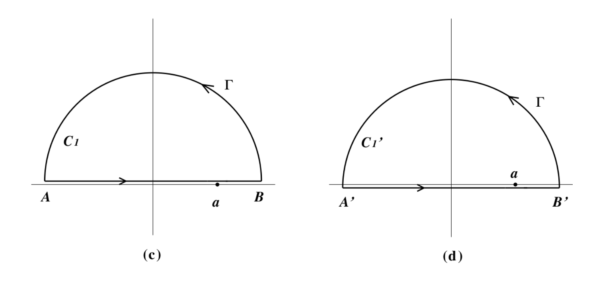
積分経路の取り方を少し変えて, 実軸から少し上または下にずらしてみる.即ち, 上図 1. の代わりに 下図 2. (a) のように \(AB\) の部分は \(z=x+i\varepsilon\) としてみる. \(\varepsilon\) を十分小さく取り, 実軸と \(AB\) の間には \(f(z)\) の特異点は含まれないとすれば, 2つの閉曲線 \(C\) と \(C_1\) に関する積分は一致する.従って次の等式が得られる:
\begin{equation}
\lim_{\varepsilon\to+0}\int_{-\infty}^{\infty}\frac{f(x)}{x-a+i\varepsilon}\,dx
=\mathrm{P}\int_{-\infty}^{\infty}\frac{f(x)}{x-a}\,dx\,-i\pi\,f(a)
\tag{7}
\end{equation}
\lim_{\varepsilon\to+0}\int_{-\infty}^{\infty}\frac{f(x)}{x-a+i\varepsilon}\,dx
=\mathrm{P}\int_{-\infty}^{\infty}\frac{f(x)}{x-a}\,dx\,-i\pi\,f(a)
\tag{7}
\end{equation}
同様に, 直線部分を下にずらして, 図 (d)のように区間 \(A’ B’\) を \(z=x-i\varepsilon\) として積分しても, \(C’\) と \(C’_{1}\) に関する積分は不変であろう.従って, 次に書ける:
\begin{equation}
\lim_{\varepsilon\to+0}\int_{-\infty}^{\infty}\frac{f(x)}{x-a-i\varepsilon}\,dx
=\mathrm{P}\int_{-\infty}^{\infty}\frac{f(x)}{x-a}\,dx\,+i\pi\,f(a)
\tag{8}
\end{equation}
\lim_{\varepsilon\to+0}\int_{-\infty}^{\infty}\frac{f(x)}{x-a-i\varepsilon}\,dx
=\mathrm{P}\int_{-\infty}^{\infty}\frac{f(x)}{x-a}\,dx\,+i\pi\,f(a)
\tag{8}
\end{equation}
この式は, 第6章の式 (6-109) を導出する際に利用することが出来る.
上記の積分関係は, 記号的に次のように書かれることがある:
\begin{equation}
\lim_{\varepsilon\to+0} \frac{1}{x-a\pm i\varepsilon}=\mathrm{P} \frac{1}{x-a}\,dx\,\mp i\pi\,\delta(x-a)
\tag{9}
\end{equation}
\lim_{\varepsilon\to+0} \frac{1}{x-a\pm i\varepsilon}=\mathrm{P} \frac{1}{x-a}\,dx\,\mp i\pi\,\delta(x-a)
\tag{9}
\end{equation}
この両辺に \(f(x)\) を掛けて, 区間 \((-\infty,\infty)\) で積分すれば上の両式が得られるという意味である:
\begin{equation}
\lim_{\varepsilon\to+0}\int_{-\infty}^{\infty} \frac{f(x)}{x-a\pm i\varepsilon}\,dx
=\mathrm{P}\int_{-\infty}^{\infty}\frac{f(x)}{x-a}\,dx\,\mp i\pi\,f(a)
\tag{10}
\end{equation}
\lim_{\varepsilon\to+0}\int_{-\infty}^{\infty} \frac{f(x)}{x-a\pm i\varepsilon}\,dx
=\mathrm{P}\int_{-\infty}^{\infty}\frac{f(x)}{x-a}\,dx\,\mp i\pi\,f(a)
\tag{10}
\end{equation}
式 (9) において \(a=0\) としてから全体に \(i\) を掛け合わせ \(x\Rightarrow\omega\) と記した場合が, 第5章の式 (5-17) である:
\begin{equation}
\lim_{\varepsilon\to+0}\frac{i}{\omega+i\varepsilon}=\mathrm{P}\frac{i}{\omega}\,d\omega\,+\pi\,\delta(\omega)
\tag{5-17}
\end{equation}
\lim_{\varepsilon\to+0}\frac{i}{\omega+i\varepsilon}=\mathrm{P}\frac{i}{\omega}\,d\omega\,+\pi\,\delta(\omega)
\tag{5-17}
\end{equation}
上式 (5-17) は「ヘビサイドの単位関数 (Heaviside unit function)」または「単位階段関数(unit step function)」: \(u(t)\) のフーリエ変換と見做すことも出来る事に注意するべし:
\begin{equation}
\mathscr{F}[u(t)]=\int_{-\infty}^{\infty}u(t)e^{-j\omega t}\,dt=\int_0^{\infty}e^{-j\omega t}\,dt
=\pi\,\delta(\omega)+\frac{1}{j\omega},\quad\leftarrow\quad u(t)=\begin{cases}1& t>0\\ 0 & t<0\end{cases}
\tag{11}
\end{equation}
\mathscr{F}[u(t)]=\int_{-\infty}^{\infty}u(t)e^{-j\omega t}\,dt=\int_0^{\infty}e^{-j\omega t}\,dt
=\pi\,\delta(\omega)+\frac{1}{j\omega},\quad\leftarrow\quad u(t)=\begin{cases}1& t>0\\ 0 & t<0\end{cases}
\tag{11}
\end{equation}
その詳しい議論は, 例えば H.P.スウ:「フーリエ解析」の § 5.4 を参照すべし.