前述した「コヒーレント状態」の波動関数は,「形が拡がらずに前後に運動する波束となる」ことが期待される．実際, コヒーレント状態の波動関数は, そのような時間変化をするであろうか？．詳しく調べて見よう．
\(\)
前述のブログ記事から, \(|\alpha\rangle\) の時間発展は次であった：
\begin{align}
\def\bra#1{\langle #1 |}
\def\ket#1{| #1 \rangle}
\def\BraKet#1#2#3{\langle #1 | #2 | #3 \rangle}
\def\BK#1#2{\langle #1 | #2 \rangle}
\def\mb#1{\mathbf{#1}}
e^{-i\hat{H}t/\hbar}\ket{\alpha}&=e^{-\frac{|\alpha|^{2}}{2}}\sum_n \frac{\alpha^{n}}{\sqrt{n!}}
e^{-i\left(n+\frac{1}{2}\right)\omega t}\ket{n}
=e^{i\frac{1}{2}\omega t}\,e^{-\frac{|\alpha|^{2}}{2}}\sum_n
\frac{(\alpha\,e^{-i\omega t})^{n}}{\sqrt{n!}}\ket{n}
\tag{3.117}
\end{align}
\def\bra#1{\langle #1 |}
\def\ket#1{| #1 \rangle}
\def\BraKet#1#2#3{\langle #1 | #2 | #3 \rangle}
\def\BK#1#2{\langle #1 | #2 \rangle}
\def\mb#1{\mathbf{#1}}
e^{-i\hat{H}t/\hbar}\ket{\alpha}&=e^{-\frac{|\alpha|^{2}}{2}}\sum_n \frac{\alpha^{n}}{\sqrt{n!}}
e^{-i\left(n+\frac{1}{2}\right)\omega t}\ket{n}
=e^{i\frac{1}{2}\omega t}\,e^{-\frac{|\alpha|^{2}}{2}}\sum_n
\frac{(\alpha\,e^{-i\omega t})^{n}}{\sqrt{n!}}\ket{n}
\tag{3.117}
\end{align}
また, 個数状態の波動関数 \(\psi_n(q)=\BK{q}{n}\) の具体的な形は次であった：
\begin{equation}
\psi_{n}(q)=\BK{q}{n}=\frac{1}{\pi^{1/4}\sqrt{2^{n}n!}}\,\exp\left(-\frac{q^{2}}{2}\right)H_n(q)
\tag{1}
\end{equation}
\psi_{n}(q)=\BK{q}{n}=\frac{1}{\pi^{1/4}\sqrt{2^{n}n!}}\,\exp\left(-\frac{q^{2}}{2}\right)H_n(q)
\tag{1}
\end{equation}
従って, 上式 (3.117) に左から \(\bra{q}\) を掛け合わせ, 式 (1) を代入することで, コヒーレント状態の波動関数
\(\psi_{\alpha}(q,t)\) は次のように求まる：
\begin{align*}
\psi_{\alpha}(q,t)&=\BraKet{q}{e^{-i\hat{H}t/\hbar}}{\alpha}
=e^{i\frac{1}{2}\omega t}\,e^{-\frac{|\alpha|^{2}}{2}}\sum_n
\frac{(\alpha\,e^{-i\omega t})^{n}}{\sqrt{n!}}\BK{q}{n}\\
&=e^{i\frac{1}{2}\omega t}\,e^{-\frac{|\alpha|^{2}}{2}}\sum_n
\frac{\alpha^{n}e^{-in\omega t}}{\sqrt{n!}}
\cdot\frac{1}{\pi^{1/4}\sqrt{2^{n}n!}}\,e^{-\frac{q^{2}}{2}}\,H_n(q)\\
&=e^{i\frac{1}{2}\omega t}\,e^{-\frac{|\alpha|^{2}}{2}}\,e^{-\frac{q^{2}}{2}}
\frac{1}{\pi^{1/4}}\sum_n\frac{\alpha^{n}e^{-in\omega t}}{\sqrt{2^{n}}\,n!}\,H_n(q)
\end{align*}
ここで, 一般に \(\alpha\) は複素数であるから \(\alpha=|\alpha|e^{i\phi}\) として次と置く：
\begin{equation}
z\equiv \frac{\alpha e^{-i\omega t}}{\sqrt{2}}=\frac{|\alpha|\,e^{-i(\omega t-\phi)}}{\sqrt{2}},
\ \rightarrow\ z^{n}=\frac{\alpha^{n}\,e^{-in\omega t}}{\sqrt{2^{n}}}
\tag{2}
\end{equation}
z\equiv \frac{\alpha e^{-i\omega t}}{\sqrt{2}}=\frac{|\alpha|\,e^{-i(\omega t-\phi)}}{\sqrt{2}},
\ \rightarrow\ z^{n}=\frac{\alpha^{n}\,e^{-in\omega t}}{\sqrt{2^{n}}}
\tag{2}
\end{equation}
すると上式は次に書ける：
\begin{equation}
\psi_{\alpha}(q,t)=e^{i\frac{1}{2}\omega t}\,e^{-\frac{|\alpha|^{2}}{2}}\,e^{-\frac{q^{2}}{2}}
\frac{1}{\pi^{1/4}}\sum_n\frac{z^{n}}{n!}\,H_n(q)
\tag{3}
\end{equation}
\psi_{\alpha}(q,t)=e^{i\frac{1}{2}\omega t}\,e^{-\frac{|\alpha|^{2}}{2}}\,e^{-\frac{q^{2}}{2}}
\frac{1}{\pi^{1/4}}\sum_n\frac{z^{n}}{n!}\,H_n(q)
\tag{3}
\end{equation}
ここで更に,「エルミート多項式の母関数( generating function )」\(S(q,s)\) を利用する：
\[S(q,s)\equiv e^{q^{2}-(s-q)^{2}}=\sum_{n=0}^{\infty}\frac{H_n(q)}{n!}s^{n}\tag{4}\]
このときの\(s\) は「補助変数」と呼ばれる．すると式 (3) の最後の部分は, ちょうど補助変数 \(s=z\) の場合になっている!．よって, 式 (2) も用いることで式 (3) は次のように書ける：
\begin{align}
&\psi_{\alpha}(q,t)=e^{i\frac{1}{2}\omega t}\,e^{-\frac{|\alpha|^{2}}{2}}\,e^{-\frac{q^{2}}{2}}
\frac{1}{\pi^{1/4}}\,e^{q^{2}-(z-q)^{2}}\notag\\
&\quad =\frac{1}{\pi^{1/4}}\,\exp\left(i\frac{1}{2}\omega t\right)
\exp\left[ -\frac{1}{2}q^{2}+2zq-z^{2}-\frac{|\alpha|^{2}}{2}\right]\notag\\
&\quad =\frac{1}{\pi^{1/4}}\,\exp\left(i\frac{1}{2}\omega t\right)
\exp\left[-\frac{q^{2}}{2}+\sqrt{2}|\alpha|\,q\,e^{-i(\omega t -\phi)}-\frac{|\alpha|^{2}}{2}
\Bigl\{1+e^{-i2(\omega t-\phi)}\Bigr\}\right]\notag\\
&\quad =\frac{1}{\pi^{1/4}}\,\exp\left(i\frac{1}{2}\omega t\right)
\exp\left[-\frac{q^{2}}{2}+\sqrt{2}|\alpha|\,q\,\cos(\omega t – \phi) -\frac{|\alpha|^{2}}{2}
\bigl\{1+\cos 2(\omega t-\phi)\bigr\}\right]\notag\\
&\quad\qquad \times\exp\left[-i\sqrt{2}|\alpha|\,q\,\sin(\omega t-\phi)+i\frac{|\alpha|^{2}}{2}
\sin 2(\omega t -\phi)\right]\notag\\
&\quad =\frac{1}{\pi^{1/4}}\,\exp\left(i\frac{1}{2}\omega t\right)
\exp\left[-\frac{q^{2}}{2}+\sqrt{2}|\alpha|\,q\,\cos(\omega t – \phi) -|\alpha|^{2}
\cos^{2}(\omega t-\phi)\right]\notag\\
&\quad\qquad \times\exp\left[-i\sqrt{2}|\alpha|\,q\,\sin(\omega t-\phi)+i|\alpha|^{2}
\sin(\omega t -\phi)\cos(\omega t -\phi)\right]\notag\\
&\quad =\frac{1}{\pi^{1/4}}\,\exp\left(i\frac{1}{2}\omega t\right)
\exp\left[-\frac{1}{2}\big\{q-\sqrt{2}|\alpha|\cos(\omega t-\phi)\big\}^{2}\right]\notag\\
&\quad\qquad \times\exp\left[-i\sqrt{2}|\alpha|\,q\,\sin(\omega t-\phi)+i|\alpha|^{2}
\sin(\omega t -\phi)\cos(\omega t -\phi)\right]
\tag{5}
\end{align}
&\psi_{\alpha}(q,t)=e^{i\frac{1}{2}\omega t}\,e^{-\frac{|\alpha|^{2}}{2}}\,e^{-\frac{q^{2}}{2}}
\frac{1}{\pi^{1/4}}\,e^{q^{2}-(z-q)^{2}}\notag\\
&\quad =\frac{1}{\pi^{1/4}}\,\exp\left(i\frac{1}{2}\omega t\right)
\exp\left[ -\frac{1}{2}q^{2}+2zq-z^{2}-\frac{|\alpha|^{2}}{2}\right]\notag\\
&\quad =\frac{1}{\pi^{1/4}}\,\exp\left(i\frac{1}{2}\omega t\right)
\exp\left[-\frac{q^{2}}{2}+\sqrt{2}|\alpha|\,q\,e^{-i(\omega t -\phi)}-\frac{|\alpha|^{2}}{2}
\Bigl\{1+e^{-i2(\omega t-\phi)}\Bigr\}\right]\notag\\
&\quad =\frac{1}{\pi^{1/4}}\,\exp\left(i\frac{1}{2}\omega t\right)
\exp\left[-\frac{q^{2}}{2}+\sqrt{2}|\alpha|\,q\,\cos(\omega t – \phi) -\frac{|\alpha|^{2}}{2}
\bigl\{1+\cos 2(\omega t-\phi)\bigr\}\right]\notag\\
&\quad\qquad \times\exp\left[-i\sqrt{2}|\alpha|\,q\,\sin(\omega t-\phi)+i\frac{|\alpha|^{2}}{2}
\sin 2(\omega t -\phi)\right]\notag\\
&\quad =\frac{1}{\pi^{1/4}}\,\exp\left(i\frac{1}{2}\omega t\right)
\exp\left[-\frac{q^{2}}{2}+\sqrt{2}|\alpha|\,q\,\cos(\omega t – \phi) -|\alpha|^{2}
\cos^{2}(\omega t-\phi)\right]\notag\\
&\quad\qquad \times\exp\left[-i\sqrt{2}|\alpha|\,q\,\sin(\omega t-\phi)+i|\alpha|^{2}
\sin(\omega t -\phi)\cos(\omega t -\phi)\right]\notag\\
&\quad =\frac{1}{\pi^{1/4}}\,\exp\left(i\frac{1}{2}\omega t\right)
\exp\left[-\frac{1}{2}\big\{q-\sqrt{2}|\alpha|\cos(\omega t-\phi)\big\}^{2}\right]\notag\\
&\quad\qquad \times\exp\left[-i\sqrt{2}|\alpha|\,q\,\sin(\omega t-\phi)+i|\alpha|^{2}
\sin(\omega t -\phi)\cos(\omega t -\phi)\right]
\tag{5}
\end{align}
従って, 確率密度 \(|\psi_{\alpha}(q)|^{2}\) は次のように書ける：
\begin{equation}
|\psi_{\alpha}(q)|^{2}=\frac{1}{\sqrt{\pi}}\exp\biggl[-\Bigl\{x-\lambda\cos(\omega t-\phi)
\Bigr\}^{2}\biggr], \quad \lambda\equiv \sqrt{2}\,|\alpha|
\tag{6}
\end{equation}
|\psi_{\alpha}(q)|^{2}=\frac{1}{\sqrt{\pi}}\exp\biggl[-\Bigl\{x-\lambda\cos(\omega t-\phi)
\Bigr\}^{2}\biggr], \quad \lambda\equiv \sqrt{2}\,|\alpha|
\tag{6}
\end{equation}
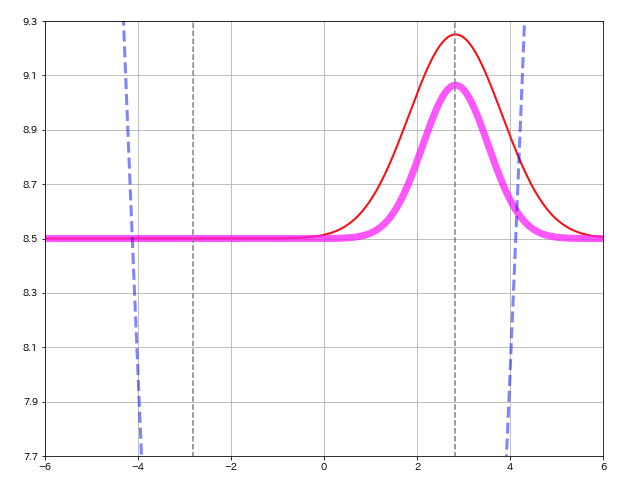
これは,『確率密度関数はガウス波束であり, その中心が「振幅が \(\lambda=\sqrt{2}\,\alpha\) である古典的な調和振動子の軌道\(y=\lambda\cos(\omega t-\phi)\) と同じ調和振動をする」ことを示している！』．そして普通ならば, 波束は時間と共に拡がることが予期されるのであるが, この特別な波束は「時間が経っても形を変えない！」ことも分かる．
このことを示すために, 式 (5) の「コヒーレント状態の波動関数」\(\psi_{\alpha}(q)\) の実数部分および式 (6) の「コヒーレント状態の確率密度」\(|\psi_{\alpha}(q)|^{2}\) を, 固有値 \(\alpha=2\) の場合でシミュレーレートするアニメーション, 及びその Python プログラムを以下に示しておく．アニメーション中, 赤線は波動関数の実数部分を表しており, 桃色の太線が確率密度関数である．
import numpy as np
import math
import matplotlib.pyplot as plt
from matplotlib import animation, rc
from IPython.display import HTML
# Figureのインスタンス生成
fig, axe = plt.subplots(1, 1, figsize=(10, 8))
amp = math.pow(math.pi, -1/4)
alpha =2
dt=1/25
T=2*math.pi/dt
time = math.ceil(2*T)
x0 = alpha*math.sqrt(2)
x = np.linspace(-6, 6, 400)
sift=x0*x0+0.5
ims = []
for t in range(time):
pt= -x0*math.sin(t*dt)
xt= x0*math.cos(t*dt)
y = amp*np.exp(-1.j*pt*xt/2-1.j*t*dt/2)*np.exp(pt*x*1.j-(x-xt)**2/2)
yy = np.conj(y)*y
im1 = axe.plot(x, y.real+sift, linewidth=2, color='red')
im2 = axe.plot(x, yy.real+sift, linewidth=7, alpha=0.7, color='magenta')
ims.append(im1+im2)
anim = animation.ArtistAnimation(fig, ims, interval=80)
# 全エネルギー E=T+V+0.5=2V+0.5=2*V(a)+0.5=2*(sqrt(2)*alpha)^2+0.5=2*alpha^2+0.5,
hy = 1/2*x*x # harmonic potential V(x)=x^2/2,
axe.plot(x,hy, color='blue', linewidth=3, alpha=0.5, linestyle="--")
rectangle = 10*np.heaviside(x+alpha*math.sqrt(2),4.5)-10*np.heaviside(x-alpha*math.sqrt(2),4.5)
axe.plot(x, rectangle, color='gray', linestyle="--") # ground state is sifted a=sqrt(2)*alpha
axe.set_xlim([-6, 6])
axe.set_ylim([sift-0.8, sift+0.8])
axe.set_yticks([7.7, 7.9, 8.1, 8.3, 8.5, 8.7, 8.9, 9.1, 9.3])
axe.grid()
#axe.legend()
# Jupyter notebookの場合は
#plt.show()
# Google Colaboratoryの場合必要
rc('animation', html='jshtml')
plt.close()
anim
【 補足 】 波動関数の周期的な時間依存性
複素数であるコヒーレント状態の波動関数 \(\psi_{\alpha}(q,t)\) は, カラー表示を利用することで表すことが出来るようだ．
そこで Wolfram Cloud によって, 複素数である式 (5) のコヒーレント状態波動関数をカラー表示でグラフ化したものを示しておく：
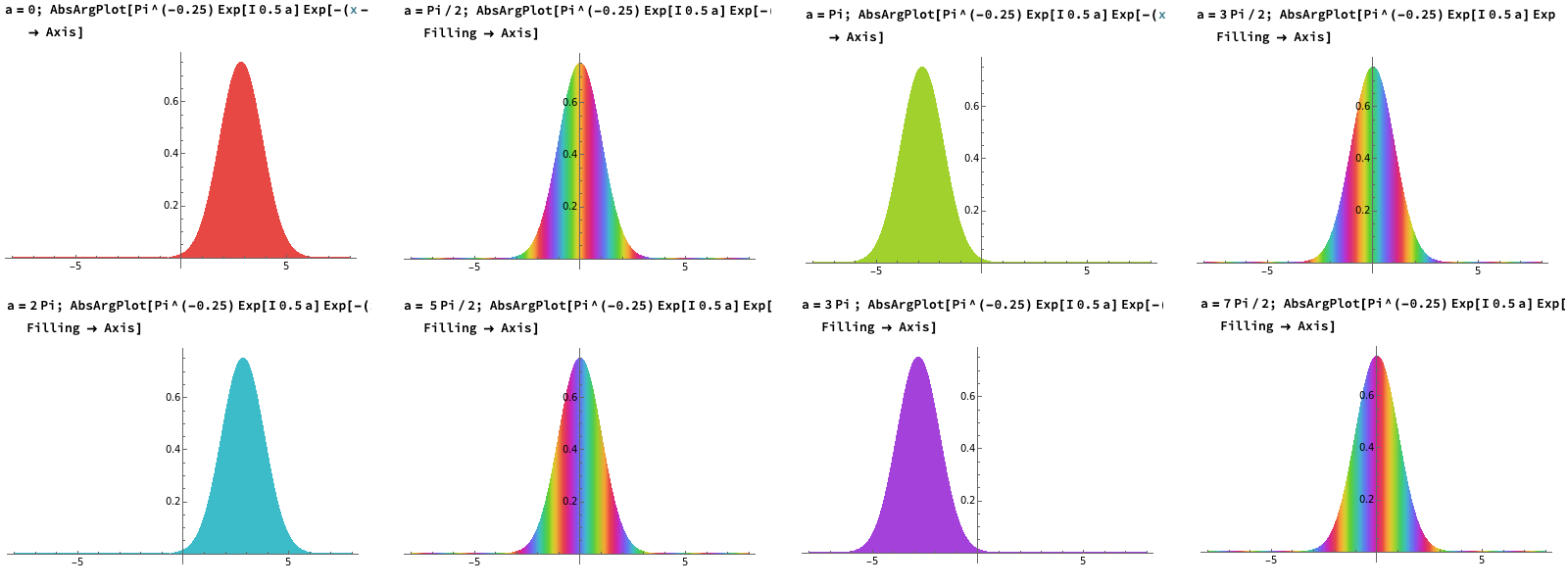
図 1. 複素数のカラー表示手法によって, コヒーレント状態の波動関数 \(\psi_{\alpha}(q,t)\) の時間変化を時間間隔 \(\Delta a=pi/2\) ごとに描いたもの．波動関数の絶対値 \(|\psi_{\alpha}(q,t)|\) はその波形で表わされ, その位相部分(偏角)はカラー(色)によって表わされている．従って, 端点の波束中で偏角が変化していない場合には純色である．しかし, 偏角が変化し振動している場合には, 色が変化するので虹色模様になっているのが分かる．
図は時間間隔 \(\Delta a=\pi/2\) ごとに描いたものである．これを見ると,「波動関数の絶対値 \(|\psi_{\alpha}(q,t)|\) の形は, 時間発展しても一定に保たれる」ことが確認される．しかし, 注意すべきは波動関数の位相を表現するその波形の色である．調和振動子の周期は \(2\pi\) であるが,「この量子力学的波動関数の周期は明らかにそうなっていない．実はその周期は \(4\pi\) となる」．そのことを「Visual Quantum Mechanics」の § 7.3.2 からの抜粋で記しておく．
7.3.2. 周期的な時間依存性
１次元調和振動子の量子力学的状態の時間発展は,「時間依存するシュレディンガー方程式」によって記述される：
\begin{equation}
i\hbar \frac{d}{dt}\psi(x,t) = H\,\psi(x,t),\quad
H=-\frac{\hbar}{2m}\frac{d^{2}}{dx^{2}}+\frac{k}{2}x^{2}
\tag{1}
\end{equation}
i\hbar \frac{d}{dt}\psi(x,t) = H\,\psi(x,t),\quad
H=-\frac{\hbar}{2m}\frac{d^{2}}{dx^{2}}+\frac{k}{2}x^{2}
\tag{1}
\end{equation}
この方程式の一般解は, そのエネルギー固有関数 \(\phi_n(x)\) の重ね合わせとして表される：
\begin{equation}
\psi(x,t)=\sum_{n=0}^{\infty} c_n e^{-iE_n t}\phi_n(x)
\tag{2}
\end{equation}
\psi(x,t)=\sum_{n=0}^{\infty} c_n e^{-iE_n t}\phi_n(x)
\tag{2}
\end{equation}
このとき, 式 (2) から次のことが言える：
【 振動状態の時間対称性 】
調和振動子ポテンシャルのシュレディンガー方程式の任意の解は次の特性を持つ：
\begin{equation}
\psi(x,t+\pi)=e^{-i\pi/2}\psi(-x,t)
\tag{7.53}
\end{equation}
従って,
\begin{equation}
\psi(x, t+2\pi)=e^{-i\pi/2}\psi(-x,t+\pi)=e^{-i\pi}\psi(x,t)=-\psi(x,t)
\tag{7.54}
\end{equation}
【 振動状態の周期的な時間依存性 】
全ての初期状態 \(\phi\) に対して, 式 (1) の解 \(\psi(x,t)\) の周期は \(T=4\pi\) である．しかし, 「波動関数」 \(\psi\) の周期は \(4\pi\) であるけれども, 量子力学的「状態」(そして特に位置の確率密度 \(|\psi(x,t)|^{2}\) ) の周期は \(2\pi\) となる．それは, 相当する古典力学系の周期に等しい．
