\(\textit{Fourth Lecture}\)
光の吸収(Absorption of Light)
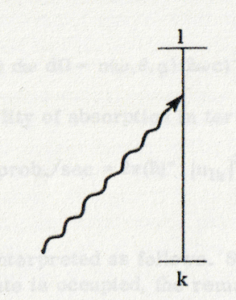
摂動理論から, 時間 \(T\) の間に状態 \(k\) から状態 \(l\) へ遷移する振幅は次式で与えられる (図4-1参照)： [1][訳註] ランダウの §34 時間に依存する摂動 によれば, 摂動方程式の解を \(\psi=\sum_k a_k(t)\psi_k^{(0)}\) … Continue reading
\begin{equation}
\def\ppdiff#1#2{\frac{\partial #1}{\partial #2}}
\def\pdiff#1{\frac{\partial}{\partial #1}}
\def\mb#1{\mathbf{#1}}
\def\reverse#1{\frac{1}{#1}}
\def\ds#1{\mbox{${\displaystyle\strut #1}$}}
a_{lk}=-\frac{i}{\hbar}\int_0^{T}\exp\left(\frac{i}{\hbar}E_l t\right)\,U_{lk}(t)\,\exp\left(-\frac{i}{\hbar}E_k t\right)\,dt
\tag{4.1}
\end{equation}
\def\ppdiff#1#2{\frac{\partial #1}{\partial #2}}
\def\pdiff#1{\frac{\partial}{\partial #1}}
\def\mb#1{\mathbf{#1}}
\def\reverse#1{\frac{1}{#1}}
\def\ds#1{\mbox{${\displaystyle\strut #1}$}}
a_{lk}=-\frac{i}{\hbar}\int_0^{T}\exp\left(\frac{i}{\hbar}E_l t\right)\,U_{lk}(t)\,\exp\left(-\frac{i}{\hbar}E_k t\right)\,dt
\tag{4.1}
\end{equation}
ただし \(U_{kl}(t)\) の時間依存性は次式のように書けば表現される：
\begin{equation}
U_{lk}(t)=u_{lk}e^{-i\omega t}
\tag{4.2}
\end{equation}
U_{lk}(t)=u_{lk}e^{-i\omega t}
\tag{4.2}
\end{equation}
(Lecture 2 の規則に合わせて指数部の引数はマイナスであり, ポテンシャルに線形な項だけが含まれている)．この時間依存性を用いて積分を実行すると,
\begin{equation}
a_{lk}=\frac{\ds{\exp\left[-\frac{i}{\hbar}\bigl\{\hbar\omega-(E_l-E_k)\bigr\}T\right]-1}}{\hbar\omega-(E_{l}-E_k)}\,u_{lk}
\tag{4.3}
\end{equation}
a_{lk}=\frac{\ds{\exp\left[-\frac{i}{\hbar}\bigl\{\hbar\omega-(E_l-E_k)\bigr\}T\right]-1}}{\hbar\omega-(E_{l}-E_k)}\,u_{lk}
\tag{4.3}
\end{equation}
遷移確率は次で与えられる：
\begin{equation}
|a_{lk}|^{2}=\frac{4\sin^{2}\left(\ds{\frac{\omega-\omega_{lk}}{2}T}\right)}{\hbar^{2}(\omega-\omega_{lk})^{2}}|u_{lk}|^{2},\qquad
\omega_{lk}=\frac{E_l-E_k}{\hbar},\quad \Delta\equiv \hbar(\omega-\omega_{lk})
\tag{4.4}
\end{equation}
|a_{lk}|^{2}=\frac{4\sin^{2}\left(\ds{\frac{\omega-\omega_{lk}}{2}T}\right)}{\hbar^{2}(\omega-\omega_{lk})^{2}}|u_{lk}|^{2},\qquad
\omega_{lk}=\frac{E_l-E_k}{\hbar},\quad \Delta\equiv \hbar(\omega-\omega_{lk})
\tag{4.4}
\end{equation}
図. 4-1
これは周波数 \(\omega\) で \((\theta,\phi)\) 方向に進む光子が吸収される確率である．光子の方向依存性は行列要素 \(u_{lk}\) 中に含まれている．例えば, 図 4-1 では電気双極子近似に於ける方向依存性を図示している．
もし入射光がある範囲の周波数と方向を含んでいるならば, すなわち次であると仮定する：
\begin{equation}
P(\omega,\theta,\phi)\,d\omega\,d\Omega
=\left\{\begin{array}{cc}
&\text{光子が周波数}\omega\text{から}\omega+d\omega\text{で}(\theta,\phi)\text{の方}\\
&\text{向周辺の立体角}d\Omega\text{に存在している確率}
\end{array}
\right\}
\tag{4.5}
\end{equation}
P(\omega,\theta,\phi)\,d\omega\,d\Omega
=\left\{\begin{array}{cc}
&\text{光子が周波数}\omega\text{から}\omega+d\omega\text{で}(\theta,\phi)\text{の方}\\
&\text{向周辺の立体角}d\Omega\text{に存在している確率}
\end{array}
\right\}
\tag{4.5}
\end{equation}
そして,「\((\theta,\phi)\) 方向を移動する光子はどれも吸収されるという確率」を欲するならば, 全ての周波数に渡って積分する必要がある．この吸収確率は次である：
\begin{equation}
\int_{0}^{\infty}d\omega\ \frac{4\sin^{2}\left(\ds{\frac{\omega-\omega_{lk}}{2}T}\right)}{\hbar^{2}(\omega-\omega_{lk})^{2}}|u_{lk}|^{2}\,P(\omega,\theta,\phi)\,d\Omega
\tag{4.6}
\end{equation}
\int_{0}^{\infty}d\omega\ \frac{4\sin^{2}\left(\ds{\frac{\omega-\omega_{lk}}{2}T}\right)}{\hbar^{2}(\omega-\omega_{lk})^{2}}|u_{lk}|^{2}\,P(\omega,\theta,\phi)\,d\Omega
\tag{4.6}
\end{equation}
\(T\) が大きいとき, 因子 \(\sin^{2}(\Delta T/2\hbar)/\Delta^2\) がかなりの値を持つのは \(\hbar\omega\) が \(E_l-E_k\) に近い場合だけであり, そして \(P(\omega,\theta,\phi)\) は, 積分に寄与する \(\omega\) の小領域に渡ってはほぼ一定となるので積分外へ出すことが許される．\(u_{lk}\) についても同様である．単位時間当たりなので \(T=1\) として, [2][訳註] ランダウの §35 に類似した議論と式がある．\(T\to\infty\) のときに次の公式が成り立つことを利用する： \begin{equation*} \lim_{T\to \infty} … Continue reading
\begin{equation}
\mathrm{Trans.prob.}=\frac{2\pi}{\hbar^{2}}\,|u_{lk}|^{2}\,\delta(\omega-\omega_{lk})\,P(\omega,\theta,\phi)\,d\Omega
=\frac{2\pi}{\hbar^{2}}\,|u_{lk}|^{2}\,P(\omega_{lk},\theta,\phi)\,d\Omega
\tag{4.7}
\end{equation}
\mathrm{Trans.prob.}=\frac{2\pi}{\hbar^{2}}\,|u_{lk}|^{2}\,\delta(\omega-\omega_{lk})\,P(\omega,\theta,\phi)\,d\Omega
=\frac{2\pi}{\hbar^{2}}\,|u_{lk}|^{2}\,P(\omega_{lk},\theta,\phi)\,d\Omega
\tag{4.7}
\end{equation}
ただし,
\begin{equation}
\hbar\omega_{lk}=E_l-E_k
\tag{4.8}
\end{equation}
\hbar\omega_{lk}=E_l-E_k
\tag{4.8}
\end{equation}
またはエネルギー範囲で考えるならば, デルタ関数の性質 \(\delta(\alpha x)=\delta(x)/\alpha\) を用いて,
\begin{align*}
\mathrm{Trans.prob.}&=\frac{2\pi}{\hbar^{2}}\,|u_{lk}|^{2}\,\delta(\omega-\omega_{lk})\,P(\omega,\theta,\phi)\,d\Omega
=\frac{2\pi}{\hbar^{2}}\,|u_{lk}|^{2}\,\delta\left\{\frac{1}{\hbar}(E-E_{lk})\right\}\,P(E,\theta,\phi)\,d\Omega\\
&=\frac{2\pi}{\hbar}\,|u_{lk}|^{2}\,\delta(E-E_{lk})\,P(E,\theta,\phi)\,d\Omega
=\frac{2\pi}{\hbar}\,|u_{lk}|^{2}\,P(E_{lk},\theta,\phi)\,d\Omega
\end{align*}
式 (4.7) は, 次のことに注意すると「入射強度」(incident intensity：単位時間に単位面積を通過するエネルギー) の表現で書くことも出来る： [3][訳註] ランダウの §69 を参照すると, 平面波の場合に於ける「ポインティングベクトル」\(\mb{S}\) (エネルギーの流れの密度)は, … Continue reading
\begin{equation}
\mathrm{Intensity} = I(\omega,\theta,\phi)\,d\Omega = \hbar\omega c\,P(\omega,\theta,\phi)\,d\Omega
\tag{4.9}
\end{equation}
\mathrm{Intensity} = I(\omega,\theta,\phi)\,d\Omega = \hbar\omega c\,P(\omega,\theta,\phi)\,d\Omega
\tag{4.9}
\end{equation}
従って,
\begin{align}
\mathrm{Trans.prob.}&=\frac{2\pi}{\hbar^{2}}\,|u_{lk}|^{2}\,
\delta(\omega-\omega_{lk})\,\frac{1}{\hbar \omega c}\,I(\omega,\theta,\phi)\,d\Omega\notag\\
&=\frac{2\pi}{\hbar^{3}\omega_{lk}c}|u_{lk}|^{2}\,I(\omega_{lk},\theta,\phi)\,d\Omega
\tag{4.10}
\end{align}
\mathrm{Trans.prob.}&=\frac{2\pi}{\hbar^{2}}\,|u_{lk}|^{2}\,
\delta(\omega-\omega_{lk})\,\frac{1}{\hbar \omega c}\,I(\omega,\theta,\phi)\,d\Omega\notag\\
&=\frac{2\pi}{\hbar^{3}\omega_{lk}c}|u_{lk}|^{2}\,I(\omega_{lk},\theta,\phi)\,d\Omega
\tag{4.10}
\end{align}
「電気双極子近似」を用いる場合は, 式 (3.20) に \(\displaystyle a=\sqrt{\frac{2\pi\hbar c^{2}}{\omega_{lk}}}\) と \(\mb{p}_{lk}=im\omega\,\mb{x}_{lk}\) を代入して,
\begin{align}
u_{lk}&=-a\frac{e}{mc}(\mb{p}_{lk}\cdot\mb{e})=-\frac{ae}{c}\cdot i\omega (\mb{x}_{lk}\cdot\mb{e})\notag\\
&=-\sqrt{\frac{2\pi\hbar c^{2}}{\omega_{lk}}}\,\frac{e}{mc}\,(\mb{p}_{lk}\cdot \mb{e})=-i\sqrt{\frac{2\pi\hbar c^{2}}{\omega_{lk}}}\,\frac{e\omega_{lk}}{c}\,(\mb{x}_{lk}\cdot\mb{e})
\tag{4.11}
\end{align}
u_{lk}&=-a\frac{e}{mc}(\mb{p}_{lk}\cdot\mb{e})=-\frac{ae}{c}\cdot i\omega (\mb{x}_{lk}\cdot\mb{e})\notag\\
&=-\sqrt{\frac{2\pi\hbar c^{2}}{\omega_{lk}}}\,\frac{e}{mc}\,(\mb{p}_{lk}\cdot \mb{e})=-i\sqrt{\frac{2\pi\hbar c^{2}}{\omega_{lk}}}\,\frac{e\omega_{lk}}{c}\,(\mb{x}_{lk}\cdot\mb{e})
\tag{4.11}
\end{align}
従って, (単位時間当たりの)全吸収確率は次となる：
\begin{align}
\mathrm{Trans.prob.}&=\frac{2\pi}{\hbar^{3}\omega_{lk}c}\,\frac{2\pi\hbar c^{2}}{\omega_{lk}}\,\frac{e^{2}\omega_{lk}^{2}}{c^{2}}\,
(\mb{x}_{lk}\cdot\mb{e})^{2}\cdot I(\omega_{lk},\theta,\phi)\,d\Omega\notag\\
&=\frac{4\pi^{2}e^{2}}{\hbar^{2} c}\,(\mb{x}_{lk}\cdot\mb{e})^{2}\,I(\omega_{kl},\theta,\phi)\,d\Omega
\tag{4.12}
\end{align}
\mathrm{Trans.prob.}&=\frac{2\pi}{\hbar^{3}\omega_{lk}c}\,\frac{2\pi\hbar c^{2}}{\omega_{lk}}\,\frac{e^{2}\omega_{lk}^{2}}{c^{2}}\,
(\mb{x}_{lk}\cdot\mb{e})^{2}\cdot I(\omega_{lk},\theta,\phi)\,d\Omega\notag\\
&=\frac{4\pi^{2}e^{2}}{\hbar^{2} c}\,(\mb{x}_{lk}\cdot\mb{e})^{2}\,I(\omega_{kl},\theta,\phi)\,d\Omega
\tag{4.12}
\end{align}
(\(l\) から \(k\) への原子遷移に伴って起こる)「自発放射」または「自然放射」(spontaneous emission) の確率は, 式 (2.7) より
\begin{align}
&\frac{\mathrm{Trans.prob.}}{\mathrm{sec}}=\frac{2\pi}{\hbar}\Big|\,{}_{f}(\mathrm{potential})_{i}\,\Big|^{2}
\cdot \frac{\omega^{2}d\Omega}{(2\pi c)^{3}\hbar}=\frac{2\pi}{\hbar}|u_{lk}|^{2}\,\frac{\omega^{2}d\Omega}{(2\pi c)^{3}\hbar},\notag\\
&\rightarrow\quad
[ \mathrm{Probability}\ \mathrm{of}\ \mathrm{spontaneous}\ \mathrm{emission} \mathrm{/sec} ] =\frac{2\pi}{\hbar^{2}}\,\frac{1}{(2\pi c)^{3}}
\,|u_{lk}|^{2}\,\omega_{lk}^{2}\,d\Omega
\tag{4.13}
\end{align}
&\frac{\mathrm{Trans.prob.}}{\mathrm{sec}}=\frac{2\pi}{\hbar}\Big|\,{}_{f}(\mathrm{potential})_{i}\,\Big|^{2}
\cdot \frac{\omega^{2}d\Omega}{(2\pi c)^{3}\hbar}=\frac{2\pi}{\hbar}|u_{lk}|^{2}\,\frac{\omega^{2}d\Omega}{(2\pi c)^{3}\hbar},\notag\\
&\rightarrow\quad
[ \mathrm{Probability}\ \mathrm{of}\ \mathrm{spontaneous}\ \mathrm{emission} \mathrm{/sec} ] =\frac{2\pi}{\hbar^{2}}\,\frac{1}{(2\pi c)^{3}}
\,|u_{lk}|^{2}\,\omega_{lk}^{2}\,d\Omega
\tag{4.13}
\end{align}
である．この「自発放射の確率」は, 式 (1.4.7) の (\(k\) から \(l\) への原子遷移に伴って起こる)「光子吸収の確率」と関係があることは明らかである．なぜなら, 始状態と終状態とは逆であるが \(|u_{lk}|=|u_{kl}|\) であるからだ．この関係は「ある特定な光子状態が占有する確率\(n(\omega,\theta,\phi)\)」という概念による表現によって最も簡単に述べることが出来るであろう．この周波数範囲と立体角 \(d\Omega\) 中には光子状態が \(\displaystyle \frac{1}{(2\pi c)^{3}\hbar}\omega^{2}\,d\omega\,d\Omega\) だけ存在するので, ある光子がこの範囲内に存在する確率は,
\begin{equation}
P(\omega,\theta,\phi)\,d\omega\,d\Omega=n(\omega,\theta,\phi)\, \frac{1}{(2\pi c)^{3}\hbar}\omega^{2}\,d\omega\,d\Omega
\tag{4.14}
\end{equation}
P(\omega,\theta,\phi)\,d\omega\,d\Omega=n(\omega,\theta,\phi)\, \frac{1}{(2\pi c)^{3}\hbar}\omega^{2}\,d\omega\,d\Omega
\tag{4.14}
\end{equation}
「吸収確率」を \(n(\omega,\theta,\phi)\) で表現するなら,
\begin{equation}
\mathrm{Trans.prob.}=\frac{2\pi}{\hbar}\,|n_{lk}|^{2}\,n(\omega,\theta,\phi)\,\frac{1}{(2\pi c)^{3}\hbar}\omega_{kl}^{2}\,d\Omega
\tag{4.15}
\end{equation}
\mathrm{Trans.prob.}=\frac{2\pi}{\hbar}\,|n_{lk}|^{2}\,n(\omega,\theta,\phi)\,\frac{1}{(2\pi c)^{3}\hbar}\omega_{kl}^{2}\,d\Omega
\tag{4.15}
\end{equation}
この方程式は次のように解釈することが出来る．\(n(\omega,\theta,\phi)\) は「光子状態が占有される確率」であるから, 右辺の残りの項たちは「その状態に在る光子が吸収される単位秒当たりの確率」のはずである．式 (4.15) を自発放射率と比較すると次のことが分かる：
\begin{equation*}
\left\{\begin{array}{cc}
\text{ある状態から光子が吸収される単位時間当}\\ \text{たりの(その状態の1光子当たりの)確率}\ \>\,
\end{array}\right\}
=\left\{\begin{array}{cc}
\text{その状態へ光子が自発放出さ}\\ \text{れる単位時間当たりの確率 }
\end{array}\right\}
\end{equation*}
\left\{\begin{array}{cc}
\text{ある状態から光子が吸収される単位時間当}\\ \text{たりの(その状態の1光子当たりの)確率}\ \>\,
\end{array}\right\}
=\left\{\begin{array}{cc}
\text{その状態へ光子が自発放出さ}\\ \text{れる単位時間当たりの確率 }
\end{array}\right\}
\end{equation*}
もし \(n(\omega,\theta,\phi)\) を状態毎の「光子の平均数」とすれば, 状態毎に複数の光子が存在する可能性がある場合でも, 式 (4.15) は正しいことを以下で示すことにしよう．
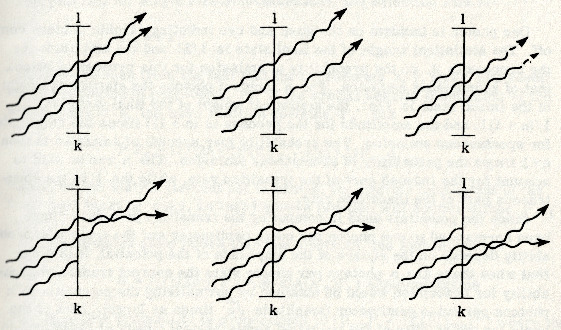
初期状態が同じ光子状態の2光子で構成されている場合, それらを区別することは出来ず, そして初期状態の統計的重みは \(1/2!\) になる!．しかし, 吸収の振幅は1光子の場合の２倍になる．このプロセスの振幅の2乗に統計的重みを掛け合わせると, 単位時間当たりの遷移確率は光子状態に１光子だけが存在する場合の「2倍になる」ことが分かる．最初の光子状態に３個の光子が存在し１個が吸収される場合には, 次の６つの過程が起こり得る (図.4-2 を参照)：
図. 4-2
入射する3光子の何れかが吸収される可能性があり, さらに吸収されない光子が入れ替わる可能性もある．初期状態の統計的な重みは \(1/3!\) であり, 最終状態の統計的な重みは \(1/2!\) である．従って遷移確率は, 初期状態に光子1個がある場合の「\((1/3!)(1/2!)(6)^{2}=3\) 倍となる」．一般に, 初期状態に \(n\) 個の光子がある場合の遷移確率は \(1\) 個の光子がある場合の遷移確率の「\(n\)倍になる」．[4][訳註] 本文の計算を \(n\) 個の場合で考える．まず最初の光子状態に \(n\) 個の光子が存在しその内の1個が吸収される場合の数は, … Continue reading
従って,「\(n(\omega,\theta,\phi)\) は１状態あたりの平均光子数である」とすれば式 (4.15) は正しいと言える．
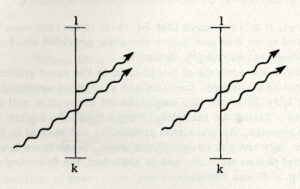
光子の放出をもたらす遷移は, 入射放射線によって誘発されることがある．このような過程 (1個の入射光子が関与) は 図 4-3 のように図式化することが出来る．
図. 4-3
1つの光子が原子に入射し, 2つの区別できない光子が放出される．最終状態の統計的な重みは \(1/2!\) であり, この過程の振幅は \(2\) であるので, この過程の放出確率は自然放出の2倍である．入射光子が \(n\) 個の場合, 初期状態の統計的重みは \(1/n!\) で, 最終状態の統計的重みは \(1/(n+1)!\), そして過程の振幅は自然放射の振幅の \((n +1)!\) 倍になる．放射の(単位秒あたりの)確率は, 自然放射の確率の \(n+1\) 倍となる．\(n\) は遷移率の誘導部分に依ると言え, 他方 \(1\) は遷移率の自発部分に依ると言える．
遷移確率の計算に使われたポテンシャルは1立方センチメートル当たり1光子に正規化されており, 遷移確率はポテンシャルの振幅の2乗に依存するので, 1光子状態あたり \(n\) 光子がある場合では, 吸収の正しい遷移確率は, ポテンシャルの正規化を1立方センチメートル当たり \(n\) 光子 (振幅は \(\sqrt{n}\) 倍) にすることで得られることは明らかである．これがいわゆる「輻射の半古典理論」の妥当性の根拠である．この理論では, 吸収は「場の実際のエネルギーに正規化されたポテンシャルによる摂動, つまり \(n\) 個の光子がある場合はエネルギーが \(n\hbar\omega\) に正規化されたポテンシャルによる摂動」から生じるとして計算される．しかし, 放射の正しい遷移確率は \(n+1\) に比例するため, それをこの方法で得ることは出来ない．その誤差は, 自発放射による遷移確率を省略したことに相当する．輻射の半古典理論では, 放射確率の自発的な部分は一般的な議論によって導出される．それには, 自発放射を考慮すると「観測されるプランク分布式が導出できる」という事実も含まれる．これらの関係を, 半古典的理論の推論から最初に導き出したのはアインシュタインである．
References
| ↑1 | [訳註] ランダウの §34 時間に依存する摂動 によれば, 摂動方程式の解を \(\psi=\sum_k a_k(t)\psi_k^{(0)}\) とした時, \begin{align*} &i\hbar\frac{da_k^{(1)}}{dt}=V_{ki}(t),\quad\rightarrow\quad a_{ki}^{(1)}=-\frac{i}{\hbar}\int V_{ki}(t)\,dt =-\frac{i}{\hbar}\int V_{ki}\,e^{i\omega_{ki}t}\,dt,\quad \text{where}\quad \omega_{ki}=\frac{E_k-E_i}{\hbar},\\ &\Rightarrow\quad a_{lk}=-\frac{i}{\hbar}\int U_{lk}(t)\,\exp\bigl\{i(E_l-E_k)t/\hbar\bigr\}\,dt =-\frac{i}{\hbar}\int e^{iE_l t/\hbar}\,U_{lk}(t)\,e^{-iE_k t/\hbar}\,dt \end{align*} |
|---|---|
| ↑2 | [訳註] ランダウの §35 に類似した議論と式がある．\(T\to\infty\) のときに次の公式が成り立つことを利用する： \begin{equation*} \lim_{T\to \infty} \frac{\sin^{2}\alpha T}{\pi T \alpha^{2}}=\delta(\alpha) \end{equation*} すると \(T\to\infty\) のとき, 式 (1.4.4) は \(\alpha=(\omega-\omega_{lk})/2\) として, \begin{align*} |a_{lk}|^{2}&=\frac{4\sin^{2}\left(\ds{\frac{\omega-\omega_{lk}}{2}T}\right)}{\hbar^{2}(\omega-\omega_{lk})^{2}}|u_{lk}|^{2} =\frac{\pi T}{\hbar^{2}}\cdot\frac{\sin^{2}\alpha T}{\pi T \alpha^{2}}|u_{lk}|^{2}=\frac{\pi T}{\hbar^{2}}|u_{lk}|^{2}\,\delta(\alpha) =\frac{\pi T}{\hbar^{2}}|u_{lk}|^{2}\,\delta\left\{\frac{1}{2}(\omega-\omega_{lk})\right\} \end{align*} 従って式 (1.4.6) は, \begin{align*} \int_0^{\infty}|a_{lk}|^{2}\,P(\omega,\theta,\phi)\,d\Omega\,d\omega &\approx |u_{lk}|^{2}\,d\Omega\,\frac{\pi T}{\hbar^{2}} \int_{0}^{\infty}P(\omega,\theta,\phi)\,\delta\left\{\frac{1}{2}(\omega-\omega_{lk})\right\}\,d\omega\\ &=\frac{\pi T}{\hbar^{2}}|u_{lk}|^{2}\,d\Omega\,2\int_{0}^{\infty}P(\omega,\theta,\phi)\,\delta(\omega-\omega_{lk})\,d\omega =\frac{2\pi T}{\hbar^{2}}|u_{lk}|^{2}\,P(\omega_{lk},\theta,\phi)\,d\Omega \end{align*} |
| ↑3 | [訳註] ランダウの §69 を参照すると, 平面波の場合に於ける「ポインティングベクトル」\(\mb{S}\) (エネルギーの流れの密度)は, 波の伝搬方向の単位ベクトルを \(\mb{n}\), エネルギー密度を \(W\) とすると, \begin{equation*} \mb{S}=\frac{c}{4\pi}\mb{E}\times\mb{H}=\frac{c}{4\pi}E^{2}\mb{n}=\frac{c}{4\pi}H^{2}\mb{n},\quad W=\frac{E^{2}+H^{2}}{8\pi},\quad \mb{S}=cW\mb{n} \end{equation*} この \(\mb{S}\) の大きさ, すなわち「輻射強度」は, 本書の場合では「エネルギー密度の平均を \(\overline{W}=\hbar\omega\) とした!」ので, \begin{equation*} |\mb{S}|=c\overline{W}=\hbar\omega\,c \end{equation*} |
| ↑4 | [訳註] 本文の計算を \(n\) 個の場合で考える．まず最初の光子状態に \(n\) 個の光子が存在しその内の1個が吸収される場合の数は, 一個が吸収された後は \(n-1\) 個が残り, それらが互いに入れ替わる場合の数が \((n-1)!\) 通りある．従って, それらを吸収される光子を選ぶ場合の数 \(n\) に掛け合わせればよいので \(n\times(n-1)!\) 通り, 即ち \(n!\) 通りである．その内で入射する \(n\) 光子は同じ光子状態に在り, 吸収過程が終わった後に残る \((n-1)\) 個の光子たちも同じ光子状態にある．従って, 遷移確率は \(n\) 倍となる： \begin{equation*} \frac{(n\times(n-1)!)^{2}}{n!(n-1)!}=\frac{n!\times n!}{n!\times(n-1)!}=\frac{n!}{(n-1)!}=n \end{equation*} |
