 経路積分問題
経路積分問題 問題 8-4 の解答例
Problem 8-4Show that the ground-state wave function for the lagrangian of Eq. (8-78) can be written\begin{equation}\Phi_...
 経路積分問題
経路積分問題  経路積分問題
経路積分問題 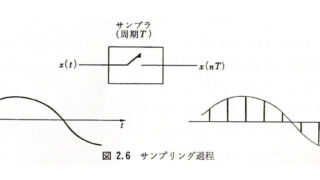 物理一般
物理一般  物理一般
物理一般  ファインマン
ファインマン  経路積分問題
経路積分問題  経路積分問題
経路積分問題  ファインマン
ファインマン  ファインマン
ファインマン  物理一般
物理一般  経路積分問題
経路積分問題  経路積分問題
経路積分問題