 経路積分問題
経路積分問題 問題 6-3 の解答例
Problem 6-3For a free particle, Eq. (4-29) reduces to\begin{equation}\def\pdiff#1{\frac{\partial}{\partial #1}}\def\Bpdi...
 経路積分問題
経路積分問題  経路積分問題
経路積分問題  経路積分問題
経路積分問題  経路積分問題
経路積分問題  経路積分問題
経路積分問題  経路積分問題
経路積分問題  物理一般
物理一般 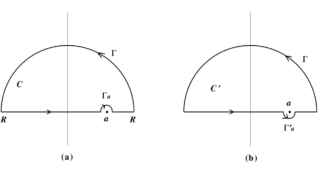 物理一般
物理一般  物理一般
物理一般  経路積分問題
経路積分問題  経路積分問題
経路積分問題  物理一般
物理一般