 物理一般
物理一般 ラグランジュ形式の場の理論
問題 8-7 は,「場の理論」に関係している.そこで, F. Mandel著:「Quantum Field Theory」から第2章の「ラグランジュ形式の場の理論」などから関係する部分を抜粋し要約したものを示しておく.2 ラグランジ形式の場...
 物理一般
物理一般 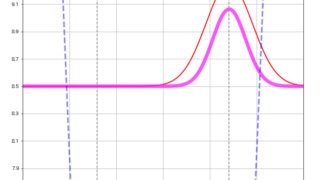 パソコン
パソコン 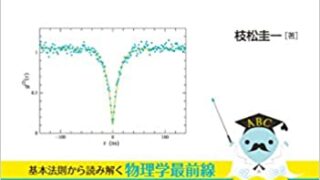 物理一般
物理一般  物理一般
物理一般  物理一般
物理一般  パソコン
パソコン  物理一般
物理一般 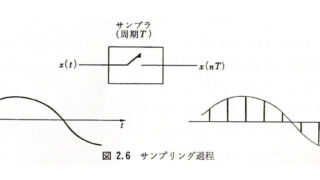 物理一般
物理一般  物理一般
物理一般  物理一般
物理一般  物理一般
物理一般  物理一般
物理一般